Question

In a right triangle ABC in which \[B = 90^\circ \] , a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Then the tangent to the circle at P bisects BC.
A. True
B. False

Answer 1

Hint: In the above given question, we are given a statement related to geometry. We have to determine if the given statement is true or false. In the statement, we are given a right angled triangle, right angled at B, where a circle is drawn with the side AB as diameter. The circle intersects the hypotenuse AC at a point P. Then a tangent is drawn to the circle at point P. We have to check if that tangent bisects the third side BC or not. In order to approach the solution, we need to recall a few properties of circles and triangles.

Complete step by step answer:
According to the given information, the diagram of the given triangle and circle can be drawn as below:

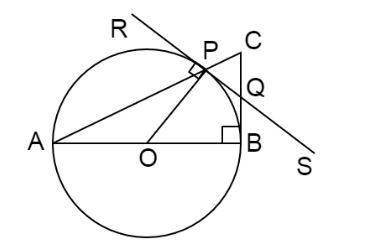
Let the tangent at P meet BC at Q. We have to prove that Q is the midpoint of BC.
\[CQ = BQ\]
Now, PQ and BQ are tangents to the circle from an external point Q, hence by that property of circles we have equal tangents PQ and BQ, i.e.
\[ \Rightarrow PQ = BQ\] ...(1)

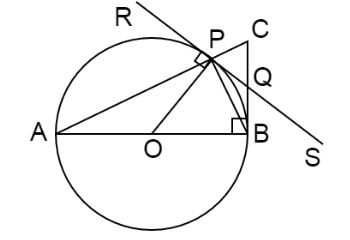
Now join the line PB, so we have the diagram as:

Now in the triangle PQB, we have \[PQ = BQ\]. Since angles opposite to equal sides are also equal in a triangle, therefore we have
\[ \Rightarrow \angle PBQ = \angle BPQ\] ...(2)
Since AB is the diameter, therefore \[\angle APB = 90^\circ \]
So we have,
\[ \Rightarrow \angle APB + \angle BPC = 180^\circ \]
\[ \Rightarrow \angle BPC = 180^\circ - 90^\circ \]
Hence,
\[ \Rightarrow \angle BPC = 90^\circ \]
Also,
\[ \Rightarrow \angle BPC = \angle BPQ + \angle QPC\]
i.e.
\[ \Rightarrow \angle BPQ + \angle QPC = 90^\circ \] ...(3)

Also in triangle PBC, we have
\[ \Rightarrow \angle PBC + \angle PCB + \angle BPC = 180^\circ \]
\[ \Rightarrow \angle PBC + \angle PCB = 180^\circ - 90^\circ \]
Hence,
\[ \Rightarrow \angle PBC + \angle PCB = 90^\circ \] ...(4)
Now from equation (3) and (4), we have
\[ \Rightarrow \angle BPQ + \angle QPC = \angle PBC + \angle PCB = 90^\circ \]
Since, from equation (2) we have \[\angle BPQ = \angle PBQ = \angle PBC\] and also \[\angle PCB = \angle PCQ\]
Therefore we have,
\[ \Rightarrow \angle PBC + \angle QPC = \angle PBC + \angle PCQ\]
Hence, we get
\[ \Rightarrow \angle QPC = \angle PCQ\]

Now in triangle PCQ, we have
\[ \Rightarrow \angle QPC = \angle PCQ\]
Therefore, that implies
\[ \Rightarrow PQ = CQ\] ...(5)
Now from equation (1) and (5), we have
\[ \Rightarrow PQ = BQ = CQ\]
That gives,
\[ \therefore BQ = CQ\]
Hence proved. Hence, Q is the midpoint of BC.
Therefore, the tangent at P bisects BC.

So the correct answer is option A.

Note: A tangent is a line that touches the edge of a curve or circle at one point, but does not cross it. It is a straight line which touches the circle at only one point. This point is called the point of tangency. The tangent to a circle is perpendicular to the radius at the point of tangency.