Question

In an equilateral triangle ABC, D is a point on side BC such that $ BD = \dfrac{1}{3}BC $ . Prove that $ 9A{D^2} = 7A{B^2} $

Answer 1

Hint: First we will draw the required triangle naming the different points of it. Since the question is about an equilateral triangle we will try to use the basic property of an equilateral triangle that all sides of an equilateral triangle are of the same measurement. After that we will find the necessary construction to frame our answer and obtain the proof.
Formula used:
In a right angled triangle if p,b and h represent the length of perpendicular, base and hypotenuse respectively then,
 $ {p^2} + {b^2} = {h^2} $

Complete step-by-step answer:
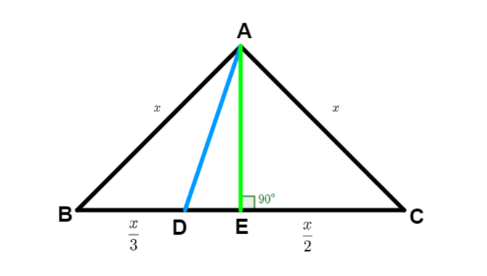
The given triangle is an equilateral triangle. Let's draw it with a point D between B and C such that $ BD = \dfrac{1}{3}BC $ . Along with this we will also draw a perpendicular AE of BC.
Since the given triangle is an equilateral triangle so let $ AB = BC = AC = x $
Consider the triangles ABE and ACE,
 $ AE = AE $ is a common side to both,
 $ \angle AEB = \angle AEC = {90^ \circ } $
And $ AB = AC = x $
So, the triangles ABE and ACE are congruent.
Thus, we have $ BE = EC = \dfrac{1}{2}BC = \dfrac{x}{2} $
Now we also have that $ BD = \dfrac{x}{3} $
Now from the image we have, $ BD + DE = BE $
 $ \Rightarrow \dfrac{x}{3} + DE = \dfrac{x}{2} \Rightarrow DE = \dfrac{x}{2} - \dfrac{x}{3} $
 $ \Rightarrow DE = \dfrac{{3x - 2x}}{6} = \dfrac{x}{6} $ --(1)

Now by using Pythagoras theorem in triangle ABE we have,
 $ A{B^2} = B{E^2} + A{E^2} $
Since the lengths of AB and BE are known to us we can put it here,
 $ \Rightarrow {x^2} = {\left( {\dfrac{x}{2}} \right)^2} + A{E^2} $
 $ \Rightarrow A{E^2} = {x^2} - {\left( {\dfrac{x}{2}} \right)^2} = {x^2} - \dfrac{{{x^2}}}{4} $
 $ \Rightarrow A{E^2} = \dfrac{{4{x^2} - {x^2}}}{4} = \dfrac{{3{x^2}}}{4} $ --(2)
Now applying Pythagoras theorem on triangle ADE we get,
\[A{D^2} = D{E^2} + A{E^2}\]
Using (1) and (2) we have,
\[A{D^2} = {\left( {\dfrac{x}{6}} \right)^2} + \dfrac{{3{x^2}}}{4}\]
\[ \Rightarrow A{D^2} = \dfrac{{{x^2}}}{{36}} + \dfrac{{3{x^2}}}{4}\]
\[ \Rightarrow A{D^2} = \dfrac{{{x^2} + 27{x^2}}}{{36}} = \dfrac{{28{x^2}}}{{36}}\]
\[ \Rightarrow A{D^2} = \dfrac{{7{x^2}}}{9}\]
\[ \Rightarrow 9A{D^2} = 7{x^2}\]
As, $ AB = BC = AC = x $
\[ \Rightarrow 9A{D^2} = 7A{B^2}\]
This proves the result that we are asked to do.

Note: Half of the answer of the proof lies on the figure, so always draw a neat and clean figure with proper labelling, this will help to understand what is given to us and what is asked of us. With a general idea in our mind we can proceed further to use various things to prove the result.