Question

In an equilateral triangle, what is the difference between the sum of the exterior angles and the sum of the interior angles?

Answer 1

Hint: We know that the sum of exterior angles is fixed for whatever be the number of sides a polygon is given in the question. Therefore, it would also be the same for triangles. For all triangles the sum of interior angles is the same, it does not depend upon what type of a triangle is given in the question.

Complete step-by-step solution:
In the given question, we have a triangle as shown below

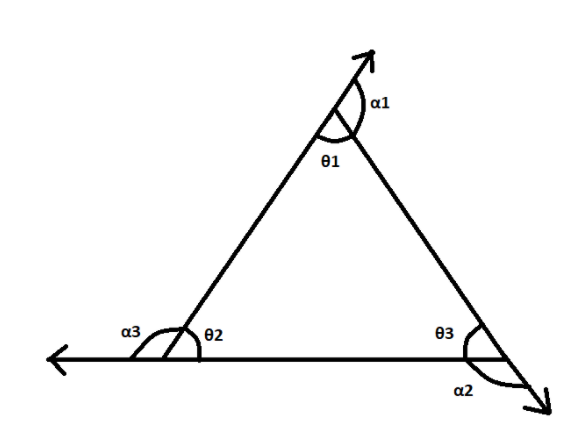
As in the above figure, we can see that \[{\theta _1},{\theta _2}\,and\,{\theta _3}\]are the interior angles of the triangle and ${\alpha _1},{\alpha _2}\,and\,{\alpha _3}$ are the exterior angles.
Also, we know that
The Sum of interior angles of any triangle (irrespective of whatever is its type i.e. equilateral, isosceles, scalene, right-angled, obtuse or acute-angled etc.) is $180$.
Also,
The sum of exterior angles of any triangle (or for that matter any polygon of any number of sides) is always $360$.
Therefore, we can say that ${\theta _1} + {\theta _2} + {\theta _3} = {180^ \circ }$ and ${\alpha _1} + {\alpha _2} + {\alpha _3} = {360^ \circ }$.
Hence, the difference between the sum of the exterior angles and the sum of the interior angles is
 $ \Rightarrow \left( {{\alpha _1} + {\alpha _2} + {\alpha _3}} \right) - \left( {{\theta _1} + {\theta _2} + {\theta _3}} \right)$
$ \Rightarrow {360^ \circ } - {180^ \circ }$
$ \Rightarrow {180^ \circ }$.

Therefore, the difference between the sum of the exterior angles and the sum of the interior angles is $180$.

Note: The exterior angles of a triangle are the angles that form a linear pair with the interior angles by extending the sides of a triangle. The sum of the exterior angles of a triangle and any polygon is 360 degrees. The remote angles are the two angles in a triangle that are not adjacent angles to a specific exterior angle. The Sum of interior angles of a polygon is always a constant value. If the polygon is regular or irregular, the sum of its interior angles remains the same. Therefore, the sum of the interior angles of the triangle is $180$ degrees.