Question

In an isosceles triangle, the altitude from the vertex bisects the base. Justify.

Answer 1

Hint:Construct an altitude from the vertex B to the base AC. Then show that the triangle AOB and COB are congruent using the SAS rule and then we get the required result using the congruence of these triangles.

Complete step-by-step answer:
We have given an isosceles triangle.
We have to show that the altitude drawn from the vertex bisects the base.
Make a figure of Isosceles triangle ABC and the figure is given as:

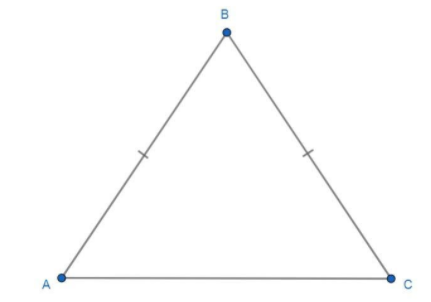
In the above figure, there is an isosceles triangle whose two sides $AB$ and$BC$ have the same length.
Now, make some constructions in the figure to carry on the required proof. We know that the altitude from the vertex is perpendicular to the base, so we have to construct an altitude from the vertex B on the base AC which intersects AC at the point O. After the construction, the figure is given as:

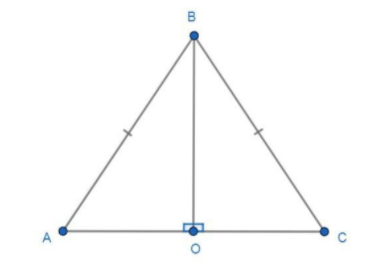
Now, take a look in the two formed triangle $ABO$ and $CBO$.
$AB = BC$ (Equal sides of Isosceles triangle)
$\angle BOC = \angle BOA$(Angle formed by altitude is$90^\circ $)
$BO = BO$(Common side of triangles)
It can be seen that the two sides and the corresponding angles are the same so, using the SAS rule of congruence, we can say that the triangles $ABO$ and $CBO$ are congruent. That is,
$\Delta AOB \cong \Delta COB$
Therefore, we can conclude that the $AO$ is equal to $CO$, which clearly shows that the altitude from the vertex bisects the base.
This is the required result that we have to prove.

Note:
This proof also gives another conclusion that the altitude from the vertex on the base bisects the angle formed at a vertex.