Question

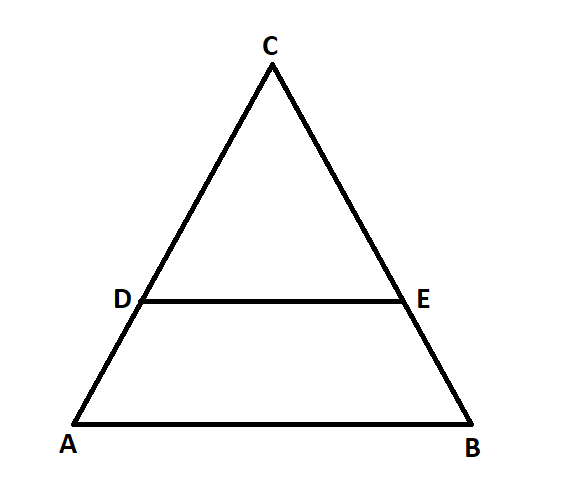
In given figure, if $\dfrac{{AD}}{{DC}} = \dfrac{{BE}}{{EC}}$ and $\angle CDE = \angle CED$, prove that $\vartriangle CAB$ is isosceles.
                        

Answer 1

Hint: To solve this question, we will use the concept of converse of basic proportionality theorem. This states that if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.

Complete step-by-step answer:
Given that,
In $\vartriangle ABC$,
 $ \Rightarrow \dfrac{{AD}}{{DC}} = \dfrac{{BE}}{{EC}}$,
Therefore, by using the converse of basic proportionality theorem,
We have,
$ \Rightarrow DE\parallel AB$
And
$ \Rightarrow \angle CDE = \angle CAB$ and [corresponding angles]
$ \Rightarrow \angle CED = \angle CBA$
And we have given,
$ \Rightarrow \angle CDE = \angle CED$ [given]
So,
$ \Rightarrow \angle CBA = \angle CAB$
Or we can say that,
$ \Rightarrow \angle B = \angle A$
We know that the sides that are opposite to equal angles are equal.
Therefore,
$ \Rightarrow BC = AC$
Hence,
$\vartriangle CAB$ is isosceles.

Note: Whenever we ask such types of questions, we have to remember the converse of basic proportionality theorem. On the other hand, the basic proportionality theorem states that if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio. It is also known as Thales theorem.