Question

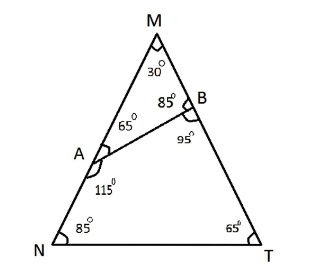
In the figure, if $\dfrac{{NT}}{{AB}} = \dfrac{9}{5}$ , and $MB = 10$ , then $MN$ will be

$
A) 18cm \\
B) 20cm \\
C) 30cm \\
D) 90cm \\
$

Answer 1

Hint: In this question, first of all observe the diagram relating with the given information in the question to get the idea about what has been asked for as an answer & how we have to proceed stepwise. For solving the question, just use similarity property for triangles which are concerned with the given sides & angles. Have a look at an angle given of the triangle and according to the relation ratio of corresponding sides are proportional to get the answer.
Given information is $NT:AB = 9:5$.

Complete step-by-step answer:
We know in similarity – If two triangles are similar with respect to angles or sides, then corresponding sides are equal.
In $\Delta AMB$ & $\Delta NMT$-
$\angle MAB = \angle MTN$- (by given figure)
$\angle AMB = \angle NMT = {30^0}$ (common angle to both triangles)
$\angle MNT = \angle MBA$ (by given figure)
$\therefore \Delta AMB \sim \Delta NMT$ i.e, $\Delta AMB$ Hence $\Delta AMB$ is congruent to $\vartriangle NMT$.
$\therefore $Hence , the two triangles $\Delta AMB$ & $\vartriangle NMT$ are similar.
As $\dfrac{{AB}}{{NT}} = \dfrac{{MB}}{{MN}}$ & $MB = 10cm$ & $NT:AB = 9:5$, putting the values of
$\therefore \dfrac{5}{9} = \dfrac{{10}}{{MN}}$
$ \Rightarrow MN = 18cm$
$\therefore $ Length of $MN = 18cm$

Note: Triangles too have a lot of properties so the concept of congruence should be clear. This question is related to a similarity topic & it is the better way to solve these questions by just proving two triangles congruent to each other with the help of given information. Don’t forget to put the unit (cm here) because a number without any unit is meaningless.