Question

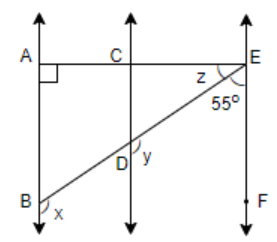
In the given figure, AB || CD and CD || EF. Also EA $\bot $ AB. If $\angle BEF={{55}^{0}}$, find the values of x, y and z.

Answer 1

Hint: Here, we will use the concept of transversal, adjacent angles and corresponding angles to find the values of x, y and z. We will also apply the concept that the sum of all the angles of a triangle is equal to 180 degrees.

Complete step-by-step answer:
In geometry, a transversal is a line that passes through two lines in the same plane at two distinct points. Transversals play a role in establishing whether two lines in a plane are parallel.
Two angles that have a common side and a common vertex (corner point) and don’t overlap are called adjacent angles. Sum of adjacent angles in 180 degrees.
When two lines are crossed by another line (which is called transversal ), the angles in matching corners are called corresponding angles. Two corresponding angles are equal to each other.
Also, according to the angle sum property of triangles, the sum of all the three angles of a triangle is equal to 180 degrees.
Here, the angle x and the angle ABE are adjacent angles. So, the sum of these two angles is equal to 180 degrees. Therefore, we can write:
$x+\angle ABE={{180}^{0}}..........\left( 1 \right)$
Now, since AB || CD and CD || EF and $\angle BAE={{90}^{0}}$, therefore, $\angle AEF={{90}^{0}}$.
That is:
$\begin{align}
  & z+{{55}^{0}}={{90}^{0}} \\
 & \Rightarrow z={{90}^{0}}-{{55}^{0}}={{35}^{0}} \\
\end{align}$
So, the value of angle z is ${{35}^{0}}$.
Now, in the triangle ABE, according to the angle sum property, we have:
$\begin{align}
  & \angle BAE+\angle AEB+\angle ABE={{180}^{0}} \\
 & \Rightarrow {{90}^{0}}+z+\angle ABE={{180}^{0}} \\
 & \Rightarrow \angle ABE={{180}^{0}}-\left( {{90}^{0}}+{{35}^{0}} \right) \\
 & \Rightarrow \angle ABE={{180}^{0}}-{{125}^{0}}={{55}^{0}} \\
\end{align}$
Therefore, the value of $\angle ABE={{55}^{0}}$.
On putting the value $\angle ABE={{55}^{0}}$ in equation (1), we get:
$\begin{align}
  & x+{{55}^{0}}={{180}^{0}} \\
 & \Rightarrow x={{180}^{0}}-{{55}^{0}} \\
 & \Rightarrow x={{125}^{0}} \\
\end{align}$
Since, x and y are corresponding angles, so they are equal.
Therefore, $y={{125}^{0}}$.
Hence, the values of x, y and z are ${{125}^{0}},{{125}^{0}}\text{ and 3}{{\text{5}}^{0}}$ respectively.

Note: Students must note here that the sum of adjacent angles is always equal to 180 degrees. Using this property only we can find the value of x. The calculations must be done properly to avoid unnecessary mistakes.