
In trapezium PQRS, given that
Answer
471.6k+ views
Hint: A quantity that has both magnitude and direction is called a vector quantity. A vector is either written in bold or is represented by an arrow above it. All the sides of the given trapezium represent a vector, from the relation between PS and QR, we can find the
Complete step-by-step answer:
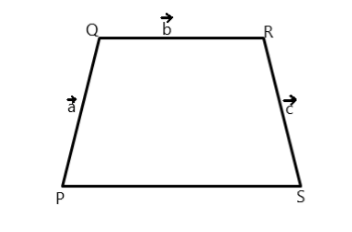
The direction of
We are given that
Now, the sum of all the vectors in a closed figure is equal to zero, so –
So, the correct answer is “
Note: If a closed polygon is formed by the set of vectors in a given order then the resultant vector is a null vector or zero vector. Using this information, we can find out the correct answer.
Complete step-by-step answer:

The direction of
We are given that
Now, the sum of all the vectors in a closed figure is equal to zero, so –
So, the correct answer is “
Note: If a closed polygon is formed by the set of vectors in a given order then the resultant vector is a null vector or zero vector. Using this information, we can find out the correct answer.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Franz thinks Will they make them sing in German even class 12 english CBSE




