Question

How many lines of symmetry does an equilateral triangle have?

Answer 1

Hint: To find the answer of this question, we should know what a line of symmetry is. A line of symmetry can be defined as the axis or the imaginary line that passes through the center of the shape or object and divides it into identical halves.

Complete step-by-step answer:

In this question, we have been asked to find the number of line symmetry an equilateral triangle has. Before proceeding with the question let us first see what a line of symmetry is. A line of symmetry can be defined as the axis or the imaginary line that passes through the center of the shape or object and divides it into identical halves.
Now, let us consider an equilateral triangle ABC and also let us consider the center of the triangle which can also be called the centroid, orthocenter, etc. as O. We know that centroid, orthocenter and incenter all lie on the same point, therefore we can take it as the center of the triangle that is O. So, we can represent it diagrammatically as follows,

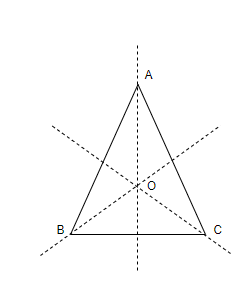
When we say that we have to divide an equilateral triangle into two congruent parts, then we think of the axis which passes through the center of the triangle that is, it passes through the point, O and also it should pass through any of the vertices of the triangle.
So, from the figure, we can see that there are 3 possible lines of symmetry which can cut the equilateral triangle into 2 congruent parts each. Thus, there are 3 lines of symmetry for an equilateral triangle.

Note: The possible mistake one can make in this question is not considering extended BO and extended CO as the lines of symmetry, because if we rotate the triangle, we will notice that only the vertices change and the rest diagram will remain the same.