Question

Prove that the base angles of an isosceles trapezium are equal.

Answer 1

Hint: We know a trapezium is a cyclic quadrilateral with one pair of parallel sides and an isosceles trapezoid has one pair of parallel sides and another pair of congruent sides (means equal in length). Equal in isosceles trapezoids in the length of the diagonal and by SSS congruence we will prove that base angles are equal.

Complete step-by-step solution:

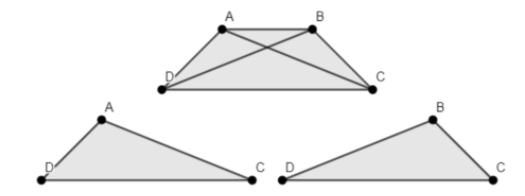
Since, a trapezium is a cyclic quadrilateral with one pair of parallel sides. An isosceles trapezoid has one pair of parallel sides and another pair of congruent sides (means equal in length). The diagonals are of equal length in isosceles trapezoid.
Draw an isosceles trapezium ABCD as drawn above.
We have to join the diagonals BD and AC in the isosceles trapezium ABCD.
By drawing the diagonals inside the trapezium we can see that $\Delta $ ADC and $\Delta $ BCD are formed.
We know we can prove equal any angles or sides of two triangles if they are congruent.
As congruency theorem is the method used to prove sides or angles are equal in the case of triangles.
In $\Delta $ ADC and $\Delta $ BCD
Here we have to know that in an isosceles trapezium is equal on opposite sides.
AD = BC
We know the diagonals are equal in an isosceles trapezium.
AC = BD
We know that the side DC is common in both the triangle implies,
DC = DC
So, we can say that by (side-side-side) SSS congruence the two triangles are congruent.
$\Delta $ ADC $ \cong $ $\Delta $ BCD (SSS postulate)
$\angle $ D = $\angle $ C (Congruence property)
Hence proved that the base angles of an isosceles trapezium are equal.

Note: In the above problem we proved that two triangles are similar by SSS postulate. If the triangle has three sides equal to the three sides of the alternate triangle, then the bases of the particular triangle are congruent, which states the SSS postulate.