Question

Prove that the bisectors of the two adjacent supplementary angles include a right angle.

Answer 1

Hint: Here in this question we must know following properties that are mentioned below: -
* Bisectors divide the angles into two equal parts.
* Sum of the interior angles of a triangle is 180 degrees.

Complete step-by-step answer:
Construction: -
Draw a line segment AB and extend point A up to point D and extend point B up to point E.
Draw bisector of $\angle DAB$ and $\angle EBA$ naming CA and BC such that lines meet at a point C.
$\angle DAB$ and $\angle EBA$ are adjacent supplementary to each other such that $\angle DAB + \angle EBA = {180^ \circ }$

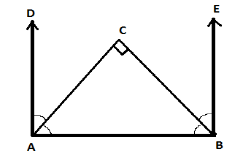
To prove: - We have to prove that the angle made after joining the bisectors is 90 degree i.e. $\angle ACB = {90^ \circ }$ or right angle.
Proof: -We have given $\angle DAB + \angle EBA = {180^ \circ }$, CA and BC are the bisectors of $\angle DAB$ and $\angle EBA$ respectively.
$\therefore \angle DAC + \angle CAB = \dfrac{1}{2}(\angle DAB)$ .....................equation 1.
$ \Rightarrow \angle EBC + \angle CBA = \dfrac{1}{2}(\angle EBA)$ .......................equation 2.
$\angle DAB + \angle EBA = {180^ \circ }$
$ \Rightarrow 2\angle CAB + 2\angle CBA = {180^ \circ }$ (Using equation 1 and 2)
$ \Rightarrow 2(\angle CAB + \angle CBA) = {180^ \circ }$ (Taking 2 common from the equation)
$ \Rightarrow (\angle CAB + \angle CBA) = {90^ \circ }$ .......................equation 3.
Now we will apply the property of triangle which states that the sum of interior angles of a triangle is 180 degrees.
$ \Rightarrow \angle CAB + \angle CBA + \angle ACB = {180^ \circ }$ (Angle sum property)
$ \Rightarrow {90^ \circ } + \angle ACB = {180^ \circ }$ (Using equation 3)
$ \Rightarrow \angle ACB = {180^ \circ } - {90^ \circ }$
$\therefore \angle ACB = {90^ \circ }$
Hence it is proved that the bisectors of the two adjacent supplementary angles include a right angle.

Note: Many students may likely make mistakes while reading and understanding the question because it is little confusing as it is not specified directly what to prove so understanding of concepts such as supplementary angles and angle bisectors must be very well known to a student. Supplementary angles are the angles which when added up gives 180 degree. They don’t have to be next to each other as long as their sum is 180 degrees they will be called as supplementary angles.