Question

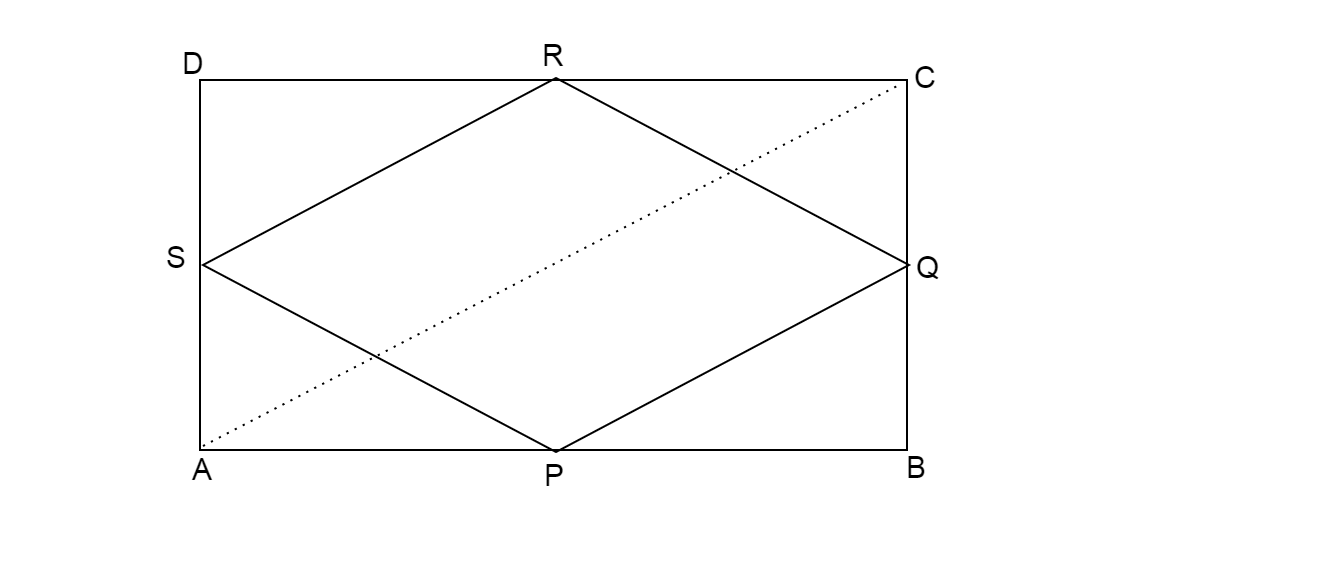
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.

Answer 1

Hint: Here we use the mid-point theorem in the two triangles formed by each diagonal and prove the quadrilateral PQRS as a parallelogram. Using SAS congruence rule we show two triangles which have adjacent sides of quadrilateral PQRS as congruent.
* Mid-point theorem: Line joining midpoints of two sides of a triangle is parallel to the third side of the triangle and is half the length of the third side of the triangle.
* SAS congruence rule states that two triangles are congruent is two sides and the included angle of a triangle is equal to corresponding two sides and the corresponding angle of the other triangle.
* Rectangle is a quadrilateral having opposite sides parallel and equal, having all interior angles as right angles.
* Rhombus is a parallelogram that has all sides equal in length.

Complete step by step answer:
In rectangle ABCD, AC and BD are the diagonals.

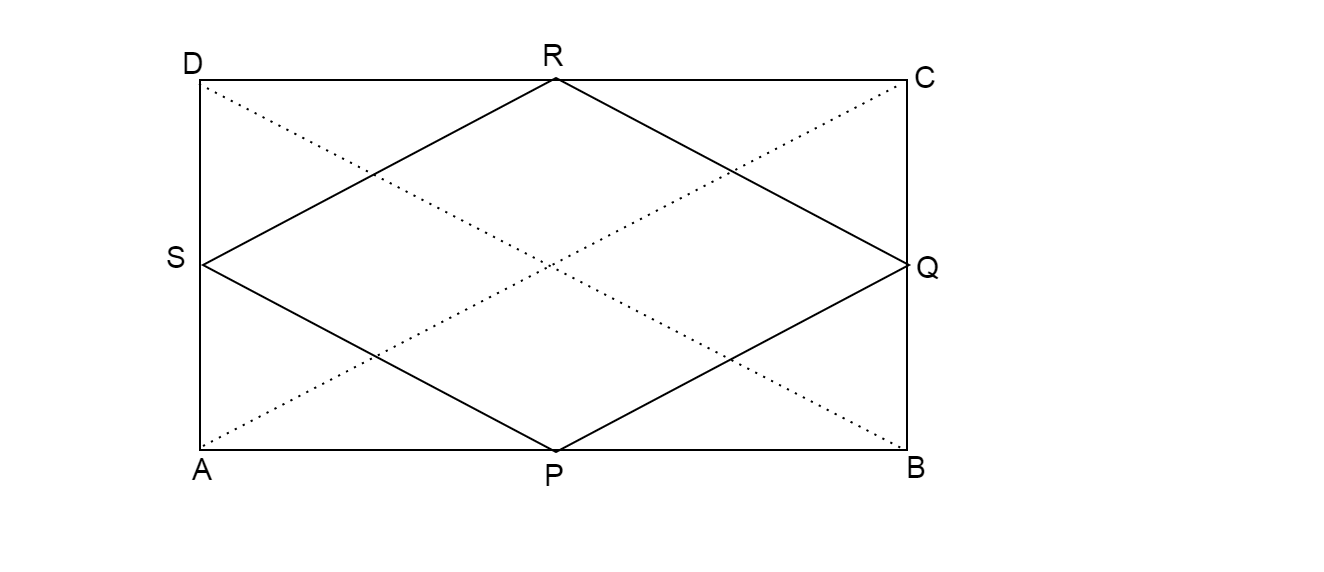
In \[\vartriangle ABC\],
P is the midpoint of AB and Q is the midpoint of BC
Using mid-point theorem, we can write
\[ \Rightarrow PQ\parallel AC\] and \[PQ = \dfrac{1}{2}AC\] ………….… (1)
In \[\vartriangle ADC\],
S is the midpoint of AD and R is the midpoint of CD
Using mid-point theorem, we can write
\[ \Rightarrow RS\parallel AC\] and \[RS = \dfrac{1}{2}AC\] ………...… (2)
From equations (1) and (2),
\[PQ\parallel RS\](As they both are parallel to the same line AC)
\[PQ = RS\](As they both are equal to \[(\dfrac{1}{2}AC)\]
\[\therefore PQ \parallel RS,PQ = RS\] ………...… (3)
In \[\vartriangle ABD\],
P is midpoint of AB and S is mid-point of AD
Using mid-point theorem, we can write
\[ \Rightarrow PS\parallel BD\] and \[PS = \dfrac{1}{2}BD\] ………...… (4)
In \[\vartriangle BCD\],
Q is midpoint of BC and R is midpoint of CD
Using mid-point theorem, we can write
\[ \Rightarrow QR\parallel BD\] and \[QR = \dfrac{1}{2}BD\] …………….… (5)
From equations (4) and (5),
\[PS\parallel QR\](As they both are parallel to the same line BD)
\[PS = QR\](As they both are equal to \[(\dfrac{1}{2}BD)\]
\[\therefore PS\parallel QR,PS = QR\] ……………….… (6)
From equations (3) and (6),
\[PQ\parallel RS,PS\parallel QR\] and \[PQ = RS,PS = QR\]
\[ \Rightarrow PQRS\] is a parallelogram
We know ABCD is a rectangle,
So, opposite sides of the rectangle ABCD must be equal to each other.
Let us consider the pair of opposite sides as AD and BC.
\[ \Rightarrow AD = BC\]
Divide both sides by 2
\[ \Rightarrow \dfrac{1}{2}AD = \dfrac{1}{2}BC\] ……………...… (7)
Since, S is mid-point of AD \[ \Rightarrow AS = SD = \dfrac{1}{2}AD\]
Similarly, Q is midpoint of BC \[ \Rightarrow BQ = QC = \dfrac{1}{2}BC\]
Substitute the value of \[\dfrac{1}{2}AD = AS,\dfrac{1}{2}BC = BQ\] in equation (7)
\[ \Rightarrow AS = BQ\] ………...… (8)
Now we prove the two triangles, \[\vartriangle PAS,\vartriangle PBQ\] congruent to each other.
In\[\vartriangle PAS,\vartriangle PBQ\],
(Since P is the midpoint of AB \[ \Rightarrow PA = PB = \dfrac{1}{2}AB\])
\[PA = PB\]
(As A and B are vertices of rectangle ABCD and rectangle has all its interior angles as \[{90^ \circ }\])
\[\angle A = \angle B\]
\[AS = BQ\](From equation (8)
\[\vartriangle PAS \cong \vartriangle PBQ\] by SAS congruence rule.
We know that the corresponding sides of congruent triangles are equal to each other.
\[ \Rightarrow PS = PQ\] ………...… (9)
We know from equations (3) and (6) \[PQ = RS,PS = QR\]
Substitute the value of \[PS = PQ\] from equation (9)
\[ \Rightarrow PQ = QR = RS = SP\]
So, all sides of the parallelogram are equal in length.

\[\therefore PQRS\] is a rhombus.

Note:
Students can make mistakes while proving the SAS congruence as they assume any two sides and any angle of one triangle equal to corresponding sides and angle of another triangle. Keep in mind we take two sides and the included angle i.e. the angle between the two sides of one triangle equal to two sides and included angle of the other triangle.