Question

How do you solve the triangle given \[A = 83^\circ 20'\], \[C = 54.6^\circ \], and \[c = 18.1\]?

Answer 1

Hint: Here, we need to find the sides and angles of the given triangle. We will use the angle sum property of a triangle to find the missing angle of the triangle. Then, we will use the law of sines to find the missing sides of the given triangle. A triangle is a two dimensional geometrical shape that has three sides.

Formula Used:
The law of sines states that in a triangle ABC, \[\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle.

Complete step-by-step answer:
First, we will convert the angle \[40^\circ 35'\] to degrees.
We can write the angle \[83^\circ 20'\] as the sum of \[83^\circ \] and \[20'\].
Therefore, we get
\[83^\circ 20' = 83^\circ + 20'\]
We will use a unitary method to convert 20 minutes to degrees.
We know that 1 degree is equal to 60 minutes.
Therefore, we get
60 minutes \[ = \] 1 degree
Dividing both sides by 60, we get
\[ \Rightarrow \]1 minute \[ = \dfrac{1}{{60}}\] degree
Multiplying both sides by 20, we get
\[ \Rightarrow \]20 minutes \[ = \dfrac{{20}}{{60}}\] degree
Simplifying the expression, we get
\[ \Rightarrow 20' = \dfrac{1}{3}\]degree
Substituting \[20' = \dfrac{1}{3}\] degree in the equation \[83^\circ 20' = 83^\circ + 20'\], we get
\[ \Rightarrow 83^\circ 20' = 83^\circ + \dfrac{1}{3}\] degree
\[ \Rightarrow 83^\circ 20' = \left( {83 + \dfrac{1}{3}} \right)\] degree
Taking the L.C.M., we get
\[ \Rightarrow 83^\circ 20' = \left( {\dfrac{{249 + 1}}{3}} \right)\] degree
Adding the terms, we get
\[ \Rightarrow 83^\circ 20' = \left( {\dfrac{{250}}{3}} \right)\] degree
Dividing 250 by 3, we get
\[ \Rightarrow 83^\circ 20' = 83.33^\circ \]
Now, we will draw the given triangle.

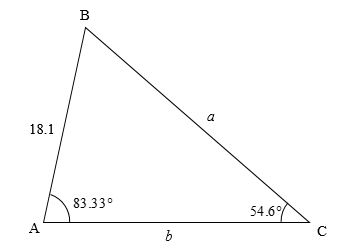
We will find the measure of angle B using the angle sum property of a triangle, that is \[A + B + C = 180^\circ \].
Substituting \[A = 83.33^\circ \] and \[C = 54.6^\circ \] in the angle sum property, we get
\[83.33^\circ + B + 54.6^\circ = 180^\circ \]
Adding the terms in the expression, we get
\[ \Rightarrow 137.93^\circ + B = 180^\circ \]
Subtracting \[137.93^\circ \] from both sides of the equation, we get
\[ \Rightarrow B = 42.07^\circ \]
Thus, we get the measure of the missing angle as \[42.07^\circ \].
Now, we will use the law of sines to find the missing lengths of the sides of the triangle.
The law of sines states that in a triangle ABC, \[\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle.
Substituting \[A = 83.33^\circ \], \[C = 54.6^\circ \], and \[c = 18.1\] in the equation \[\dfrac{{\sin A}}{a} = \dfrac{{\sin C}}{c}\], we get
\[ \Rightarrow \dfrac{{\sin 83.33^\circ }}{a} = \dfrac{{\sin 54.6^\circ }}{{18.1}}\]
Simplifying the expression, we get
\[ \Rightarrow a = 18.1 \times \dfrac{{\sin 83.33^\circ }}{{\sin 54.6^\circ }}\]
Multiplying the terms and simplifying, we get
\[ \Rightarrow a \approx 22.055\]
Substituting \[B = 42.07^\circ \], \[C = 54.6^\circ \], and \[c = 18.1\] in the equation \[\dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}\], we get
\[ \Rightarrow \dfrac{{\sin 42.07^\circ }}{b} = \dfrac{{\sin 54.6^\circ }}{{18.1}}\]
Simplifying the expression, we get
\[ \Rightarrow b = 18.1 \times \dfrac{{\sin 42.07^\circ }}{{\sin 54.6^\circ }}\]
Multiplying the terms and simplifying, we get
\[ \Rightarrow b \approx 14.878\]
Therefore, we get the missing sides of the triangle as \[a \approx 22.055\] and \[b \approx 14.878\] approximately.

Note: We used a unitary method to convert 20 minutes to degrees. Unitary method is a method where first, the per unit quantity is calculated, and then the number of units are multiplied. Here, we first calculated the value of 1 minute in degrees, and then multiplied it by 20 to get the value of 20 minutes in degrees.
We used the angle sum property of a triangle to find angle B. The angle sum property of a triangle states that the sum of the measures of the three interior angles of a triangle is always \[180^\circ \].