Question

State and verify the Euler’s formula for cube.

Answer 1

Hint: We know that Euler’s formula gave a relation between the faces, edges and vertices of the polyhedron. Euler's formula $F + V - E = 2$ , where F is the total number of Faces in the given solid, V is the total number of vertices, and E is the total number of edges. Count all of the faces, vertices, and edges, and check that the Left-Hand side of Euler's formula equals the Right-Hand side of the formula.

Complete step-by-step solution:
According to Euler’s formula for any solid, the number of Faces (F) and vertices (V) added together is exactly two more than the number of edges (E).
And the Euler’s formula is $F + V - E = 2$
Where F is faces, V is vertices and E is edges.
We must determine how many edges there are in a cuboid. So, first, draw a cube.

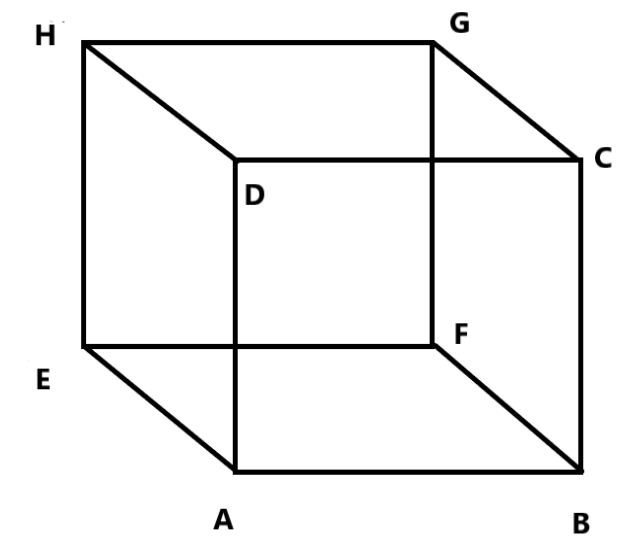
The cube's vertices are A, B, C, D, E, F, G, and H in this case.
A cube is a solid figure with six rectangular faces that are perpendicular to each other.
So, a cube has six faces, which are ABCD, DCGH, ADEH, BCGF, EFGH, and ABFE.
The cube has twelve edges AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, DH, CG.
Now, we will enter F=6 (the number of faces), E=12(number of edges) and V=8 (the number of vertices) into the given Euler's formula.
We know Euler’s formula
$ \Rightarrow F + V - E = 2$
$ \Rightarrow 6 + 8 - 12 = 2$
$ \Rightarrow 2 = 2$
Since L.H.S is R.H.S, Euler's formula is applied on the cube.

Note: Students frequently make errors when counting the number of edges and faces of 3-D figures because edges and faces usually overlap when we plot a solid on a plane and they appear to us to be a single edge or a single face.