
The area (in square units) bounded by the parabola \[y={{x}^{2}}-1,\] the tangent at the point (2, 3) to it and the y-axis is:
\[\left( a \right)\dfrac{14}{3}\]
\[\left( b \right)\dfrac{56}{3}\]
\[\left( c \right)\dfrac{8}{3}\]
\[\left( d \right)\dfrac{32}{3}\]
Answer
469.2k+ views
Hint: First, we will draw the graph of \[y={{x}^{2}}-1\] and find the equation of the tangent at (2, 3) using the differentiation. Then plot the points where these curves meet the x and y-axis. Now, apply the formula \[\int\limits_{a}^{b}{f\left( y \right)}dy-\int\limits_{c}^{d}{g\left( y \right)dy,}\] where f(y) is the equation of the tangent, ‘a’ and ‘b’ are the limits up to which the area is found, whereas g(y) is the equation of the parabola in terms of y and ‘c’ and ‘d’ are the limits up to which the area is found.
Complete step by step answer:
Here, we are provided with a parabola \[y={{x}^{2}}-1.\] Now, we have to find a tangent at the point (2, 3).
\[\Rightarrow y={{x}^{2}}-1\]
On differentiating, we get,
\[\Rightarrow \dfrac{dy}{dx}=2x-0\]
\[\Rightarrow \dfrac{dy}{dx}=2x\]
At point (2, 3), we have,
\[\Rightarrow \dfrac{dy}{dx}=2\times 2=4\]
Therefore, the slope of tangent = 4.
Let us assume the equation of the tangent as y = mx + c, where m is the slope and c is the intercept on the y-axis. On substituting the value of slope (m) = 4, we get,
\[y=4x+c.....\left( i \right)\]
Since this line passes through the point (2, 3), therefore it satisfies the point (2, 3). So, substituting (2, 3) in equation (i), we get,
\[\Rightarrow 3=8+c\]
\[\Rightarrow c=-5\]
So, the equation of tangent becomes
\[\Rightarrow y=4x-5\]
Now, let us plot the graph for these curves. We have,
\[\left( 1 \right)y={{x}^{2}}-1\]
At y = 0, \[x=\pm 1\]
At x = 0, y = – 1
\[\left( 2 \right)y=4x-5\]
At y = 0, \[x=\dfrac{5}{4}\]
At x = 0, y = – 5
So, the graph can be plotted as
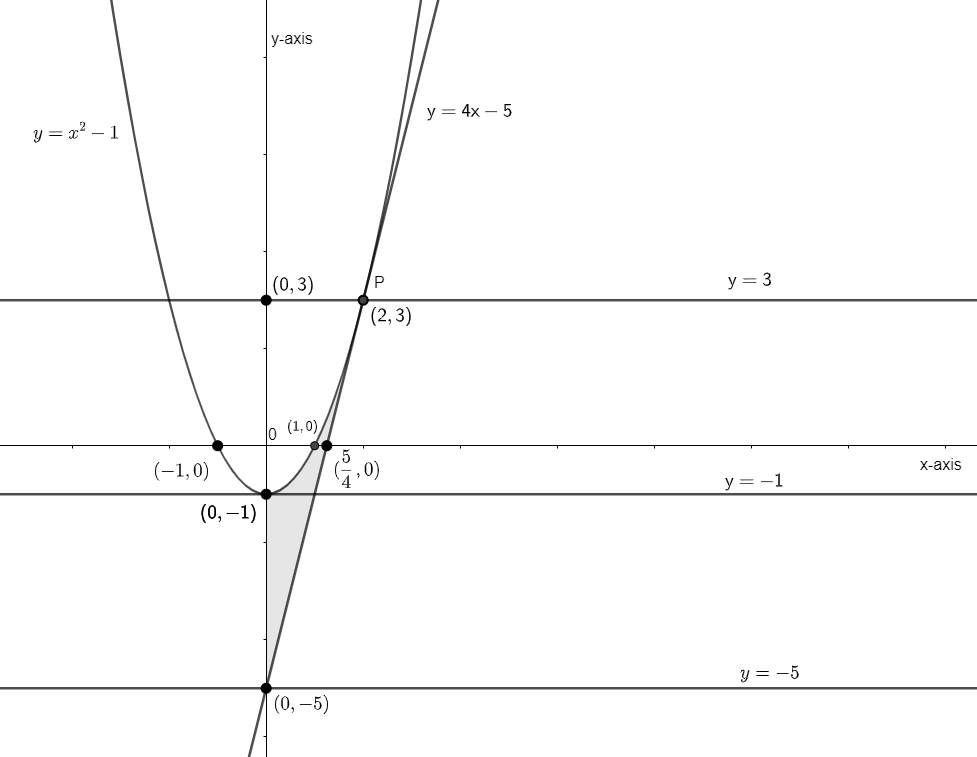
Clearly, we can see that the area required is the shaded part shown above.
\[\Rightarrow \text{Area}=\int\limits_{a}^{b}{f\left( y \right)dy}-\int\limits_{c}^{d}{g\left( y \right)dy}\]
Here, f(y) is the equation of the tangent in terms of y. So, we get,
\[f\left( y \right)=\dfrac{1}{4}\left( y+5 \right)\]
And g(y) is the equation of the parabola in terms of y. So, we get,
\[g\left( y \right)=\sqrt{y+1}\]
Here ‘a’ and ‘b’ are the limits between which the area of f(y) is calculated, i.e. (a, b) = (– 5, 3).
And ‘c’ and ‘d’ are the limits between which the area of g(y) is calculated, i.e. (c, d) = (– 1, 3).
\[\Rightarrow \text{Area}=\int\limits_{-5}^{3}{\dfrac{1}{4}\left( y+5 \right)dy}-\int\limits_{-1}^{3}{\sqrt{y+1}dy}\]
\[\Rightarrow \text{Area}=\dfrac{1}{4}\left[ \dfrac{{{y}^{2}}}{2}+5y \right]_{-5}^{3}-\dfrac{2}{3}\left[ {{\left( y+1 \right)}^{\dfrac{3}{2}}} \right]_{-1}^{3}\]
\[\Rightarrow \text{Area}=\dfrac{1}{4}\left[ \left( \dfrac{9}{2}+15 \right)-\left( \dfrac{25}{2}-25 \right) \right]-\dfrac{2}{3}\left[ {{4}^{\dfrac{3}{2}}}-0 \right]\]
\[\Rightarrow \text{Area}=\dfrac{1}{4}\left[ 32 \right]-\dfrac{2}{3}\times 8\]
\[\Rightarrow \text{Area}=\dfrac{8}{3}\]
So, the correct answer is “Option C”.
Note: One may note that plotting the graph is very important because then only we can visualize the points which are taken as limits. The important points should be marked in the graph. Also, note that we have used the formula for area, i.e. \[\text{Area}=\int{f\left( y \right)dy}\] because we have to calculate the area bounded by the y-axis. If we were to find the area bounded by the x-axis then we would have used the formula \[\int{f\left( x \right)dx}.\]
Complete step by step answer:
Here, we are provided with a parabola \[y={{x}^{2}}-1.\] Now, we have to find a tangent at the point (2, 3).
\[\Rightarrow y={{x}^{2}}-1\]
On differentiating, we get,
\[\Rightarrow \dfrac{dy}{dx}=2x-0\]
\[\Rightarrow \dfrac{dy}{dx}=2x\]
At point (2, 3), we have,
\[\Rightarrow \dfrac{dy}{dx}=2\times 2=4\]
Therefore, the slope of tangent = 4.
Let us assume the equation of the tangent as y = mx + c, where m is the slope and c is the intercept on the y-axis. On substituting the value of slope (m) = 4, we get,
\[y=4x+c.....\left( i \right)\]
Since this line passes through the point (2, 3), therefore it satisfies the point (2, 3). So, substituting (2, 3) in equation (i), we get,
\[\Rightarrow 3=8+c\]
\[\Rightarrow c=-5\]
So, the equation of tangent becomes
\[\Rightarrow y=4x-5\]
Now, let us plot the graph for these curves. We have,
\[\left( 1 \right)y={{x}^{2}}-1\]
At y = 0, \[x=\pm 1\]
At x = 0, y = – 1
\[\left( 2 \right)y=4x-5\]
At y = 0, \[x=\dfrac{5}{4}\]
At x = 0, y = – 5
So, the graph can be plotted as

Clearly, we can see that the area required is the shaded part shown above.
\[\Rightarrow \text{Area}=\int\limits_{a}^{b}{f\left( y \right)dy}-\int\limits_{c}^{d}{g\left( y \right)dy}\]
Here, f(y) is the equation of the tangent in terms of y. So, we get,
\[f\left( y \right)=\dfrac{1}{4}\left( y+5 \right)\]
And g(y) is the equation of the parabola in terms of y. So, we get,
\[g\left( y \right)=\sqrt{y+1}\]
Here ‘a’ and ‘b’ are the limits between which the area of f(y) is calculated, i.e. (a, b) = (– 5, 3).
And ‘c’ and ‘d’ are the limits between which the area of g(y) is calculated, i.e. (c, d) = (– 1, 3).
\[\Rightarrow \text{Area}=\int\limits_{-5}^{3}{\dfrac{1}{4}\left( y+5 \right)dy}-\int\limits_{-1}^{3}{\sqrt{y+1}dy}\]
\[\Rightarrow \text{Area}=\dfrac{1}{4}\left[ \dfrac{{{y}^{2}}}{2}+5y \right]_{-5}^{3}-\dfrac{2}{3}\left[ {{\left( y+1 \right)}^{\dfrac{3}{2}}} \right]_{-1}^{3}\]
\[\Rightarrow \text{Area}=\dfrac{1}{4}\left[ \left( \dfrac{9}{2}+15 \right)-\left( \dfrac{25}{2}-25 \right) \right]-\dfrac{2}{3}\left[ {{4}^{\dfrac{3}{2}}}-0 \right]\]
\[\Rightarrow \text{Area}=\dfrac{1}{4}\left[ 32 \right]-\dfrac{2}{3}\times 8\]
\[\Rightarrow \text{Area}=\dfrac{8}{3}\]
So, the correct answer is “Option C”.
Note: One may note that plotting the graph is very important because then only we can visualize the points which are taken as limits. The important points should be marked in the graph. Also, note that we have used the formula for area, i.e. \[\text{Area}=\int{f\left( y \right)dy}\] because we have to calculate the area bounded by the y-axis. If we were to find the area bounded by the x-axis then we would have used the formula \[\int{f\left( x \right)dx}.\]
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What is a transformer Explain the principle construction class 12 physics CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?

How much time does it take to bleed after eating p class 12 biology CBSE




