Question

The base and top radius of a truncated cone is 20 mm and 10 mm respectively. The height of the cone is 360 mm. What is the volume of the truncated cone? (Use π = 3)
 $
  {\text{A}}{\text{. 252,000 m}}{{\text{m}}^3} \\
  {\text{B}}{\text{. 242,000 m}}{{\text{m}}^3} \\
  {\text{C}}{\text{. 232,000 m}}{{\text{m}}^3} \\
  {\text{D}}{\text{. 222,000 m}}{{\text{m}}^3} \\
 $

Answer 1

Hint: In order to find out the volume of a truncated cone we apply the formula of the volume of a truncated cone. A truncated cone has two radii one on the upper part and one on the lower part. The height of the truncated cone is the distance between both the bases.

Complete step-by-step answer:
Given Data,
Base radius = 20 mm
Top radius = 10 mm
Height = 360 mm

A truncated cone is formed when a plane which is parallel to the base of the cone, cuts the part of the cone which has the apex resulting in forming a figure similar to the one shown below. The height of this cone becomes the line segment joining the centers of both the upper and lower bases.
Let us consider the base radius, top radius and height of this cone to be R, r and H respectively.

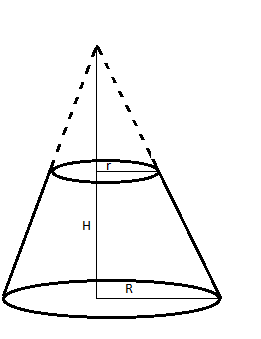
We know the volume of a truncated cone is given by the formula,
 $ {\text{V = }}\dfrac{{\pi {\text{h}}}}{3}\left( {{{\text{R}}^2} + {\text{ Rr + }}{{\text{r}}^2}} \right) $ , where the base radius, top radius and height of the cone are R, r and H respectively.
In this question, R = 20 mm, r = 10 mm, H = 360 mm
 $
   \Rightarrow {\text{V = }}\dfrac{{\pi \left( {360} \right)}}{3}\left( {{{20}^2} + {\text{ 20}}\left( {10} \right){\text{ + 1}}{{\text{0}}^2}} \right) \\
   \Rightarrow {\text{V = }}\dfrac{{\pi \left( {360} \right)}}{3}\left( {400 + {\text{200 + 100}}} \right) \\
   \Rightarrow {\text{V = }}\pi \left( {120} \right)\left( {700} \right) \\
   \Rightarrow {\text{V = 252000 cubic millimeters}} \\
 $

Therefore the volume of the truncated cone is 252,000 cubic millimeters.
Option A is the correct answer.

Note: In order to solve this type of questions the key is to know the concept of a truncated cone and the formula of volume of a truncated cone.
There are two radii in a truncated cone, so we have to be careful while substituting the base and top radii of the truncated cone.
Volume is always expressed in cubic units. Cubic millimeters can also be represented as $ {\text{m}}{{\text{m}}^3} $.