Question

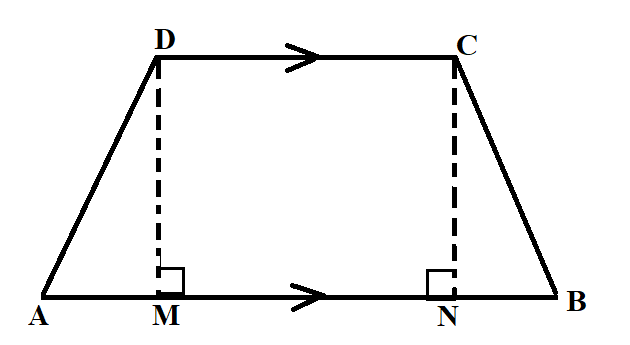
The cross-section of a perpendicular to its length is a trapezium ABCD as shown in the figure also given that:
${\text{AM = BN;AB = 7m;CD = 5m}}$. The height of the tunnel is 2.4m. The tunnel is 40m long. Calculate the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs. 5 per ${m^2}$ (sq. metre).

A.Rs. 2040
B.Rs. 3040
C.Rs. 2140
D.Rs. 2240

Answer 1

Hint: We will first find the length of AM by using the given conditions and then the length AD using Pythagoras theorem. We will prove the two right angles $\vartriangle {\text{AMD}}$ and $\vartriangle {\text{BNC}}$ as congruent and find the length of all the sides of trapezium to calculate the perimeter. Next, multiply the height of the tunnel with the perimeter to find the required area. Multiply the area of the tunnel to be painted with the cost of painting to find the total cost.

Complete step-by-step answer:
We are given a trapezium in which DM and CN are perpendiculars on AB.
Also, it is given that ${\text{CD}} = 5m$ and AM is equal to BN
The length of MN will also be 5m as DM and CN are perpendiculars on AB
Therefore, we have
$
  {\text{AM + BN}} = 7 - 5 \\
   \Rightarrow {\text{AM + BN = 2}} \\
 $
But, we have \[{\text{AM = BN}}\]
$
   \Rightarrow {\text{AM + AM}} = 2 \\
   \Rightarrow 2{\text{AM}} = 2 \\
   \Rightarrow {\text{AM}} = 1 \\
   \Rightarrow {\text{BN}} = 1 \\
 $
Now, we have to find the length of AD
Consider the triangle $\vartriangle AMD$, which is a right angle triangle.
In a right triangle the square of hypotenuse is equal to the sum of squares of other two sides by Pythagoras theorem.
Hence,
${\left( {{\text{AD}}} \right)^2} = {\left( {{\text{DM}}} \right)^2} + {\left( {{\text{AM}}} \right)^2}$
On substituting the values of DM which is given as 2.4m and the length of AM is calculated as 1m
Therefore,
$
  {\left( {{\text{AD}}} \right)^2} = {\left( {{\text{2}}{\text{.4}}} \right)^2} + {\left( 1 \right)^2} \\
   \Rightarrow {\left( {{\text{AD}}} \right)^2} = 5.76 + 1 \\
   \Rightarrow {\left( {{\text{AD}}} \right)^2} = 6.76 \\
   \Rightarrow {\text{AD}} = 2.6m \\
$
Now, $\vartriangle {\text{AMD}} \cong \vartriangle {\text{BNC}}$
As \[\angle {\text{AMD = }}\angle {\text{BNC = 9}}{{\text{0}}^ \circ }\]
\[{\text{AM = BN}}\] is given
And ${\text{DM = CN}}$as they are distances between two parallel lines.
Then, by Side-angle-side rule, $\vartriangle {\text{AMD}} \cong \vartriangle {\text{BNC}}$
Therefore, ${\text{AD = BC = 2}}{\text{.6m}}$
Now, we will calculate the perimeter of the square
As we know that the perimeter of a trapezium is the sum of all the sides of trapezium
Therefore, the perimeter is
 $
  {\text{AB + BC + CD + DA = }}\left( {{\text{7 + 2}}{\text{.6 + 5 + 2}}{\text{.6}}} \right)m \\
   = 17.2m \\
$
We are given that the height is 2.4m
The internal area of the tunnel will be perimeter multiplied by its length which is 40m long.
Also, we have to exclude the area of the floor whose length is 7m and breadth will be 40m
Hence, the required area of painting is,
$
   = 17.2\left( {40} \right) - 40\left( 7 \right) \\
   = 688 - 280 \\
   = 408{m^2} \\
$
We are given that the cost of painting is Rs. 5 per ${m^2}$, therefore to find the total cost, multiply the total area by 5
Hence, the total cost is,
$408\left( 5 \right) = Rs.2040$
Thus, option A is correct.

Note: Trapezium is quadrilateral with a pair of parallel sides known as bases of trapezium and it has a pair of non-parallel sides called legs. Here, the length of non-parallel sides are equal, therefore, it is also known as isosceles trapezium.