Question

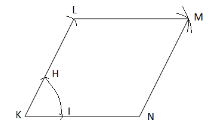
The diagram shows the construction of a parallelogram KLMN. The width of the compasses for step I and step II are the same. The value of $\angle KLM$ is:

A) $45^\circ $
B) $60^\circ $
C) $120^\circ $
D) $135^\circ $

Answer 1

Hint: First, write the steps I and II of the construction of a parallelogram. The arc will give the value of the angle. Now, use the properties of the parallelogram which is its adjacent angles are supplementary. After that substitute the value of the angle and subtract it from the total value. The output will be the desired result.

Complete step-by-step answer:
Given: - The width of the compasses for step I and step II are the same.
The steps I and II for the construction of parallelogram is,
Step I: Place the point of the compass at point K of the line and draw an arc.
Step II: Then, place the point of the compass on the point I and mark a cut on the arc at H. This measures an angle of $60^\circ $.
So, the $\angle LKN$ is $60^\circ $.
Since KLMN is a parallelogram. So, its adjacent angles are supplementary i.e., $180^\circ $.
Then,
$\angle LKN + \angle KLM = 180^\circ $
Substitute the value of the $\angle LKN$ in the equation,
$60^\circ + \angle KLM = 180^\circ $
Move $60^\circ $ to the other side and subtract from $180^\circ $,
$\angle KLM = 120^\circ $.
Thus, the value of $\angle KLM$ is $120^\circ $.

Hence, option (C) is correct.

Note: A parallelogram is a flat shape with four straight, connected sides so that opposite sides are congruent and parallel. This means a parallelogram is a plane figure, a closed shape, and a quadrilateral.
The properties of the parallelogram are:
The opposite sides are parallel.
The opposite sides are congruent.
The opposite angles are equal (congruent) to each other.
Any two adjacent angles of a parallelogram add up to $180^\circ $.