Question

The diameter of the circle is 8cm. Calculate the radius and draw a circle using this radius with the help of a compass. The radius of the circle is

Answer 1

Hint: We had to only divide the diameter of the circle by 2 to get the required radius of that circle because the diameter of the circle is always twice its radius.

Complete step-by-step answer:
As we know that the diameter of any circle is the line segment passing from the centre of the circle and the endpoint of that line segment lies on the circle. So, there can be many diameters of a circle but the length of all the diameters must be the same.
Now the radius of the circle is the line segment whose one endpoint is at the centre of the circle and the other lies on the circle. And there can also be many such line segments but the length of all of them must be the same.
So, the length of radius of the circle must be half of the length of the diameter of the circle.
Now as given in the question that the diameter of the circle is 8cm.
So, the radius of the circle must be equal to \[\dfrac{8}{2} = 4\]cm
 Now we had to draw the circle.
So, for drawing the circle of radius 4cm we had to follow some steps and that were:
First, we had to place the pencil on the compass and then open the compass up to 4cm and measure using a ruler.
Now place the pointed end of the compass at the piece of paper and move the pencil around the pointed end without disturbing it.

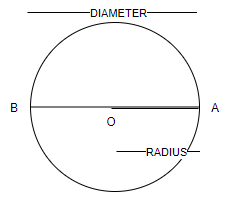
Now the required circle is drawn, and the centre of this circle will be the point where our compass point is place (i.e. O).
And radius will be the line segment joining point O and circle (i.e. OA).
And the diameter of the circle will be the line segment which passes through the centre (i.e. O) and its endpoints lies on the circle (i.e. AB).
Hence the radius of the circle will be 4cm.

Note:- Whenever we come up with this type of problem first, we have to find the radius of the circle by dividing the diameter by 2. And after that we should remember that a circle is a shape whose all points are equidistant from the centre. So, to draw a circle of x cm we had to first open the compass up to x cm and then draw the circle by placing the end point of a compass at the fixed point. This will be the easiest and efficient way to find the solution of the problem.