Question

The external length, breadth and height of a closed rectangular wooden box are 18 cm, 10 cm and 6 cm, respectively. And the thickness of wood is $\dfrac{1}{2}$ cm. When the box is empty, it weighs 15 kg and when filled with sand it weights 100 kg. The weight of a $\text{c}{{\text{m}}^{\text{3}}}$ of a wood and a $\text{c}{{\text{m}}^{\text{3}}}$ of sand are respectively.
(a) $\dfrac{1}{7}$ kg, $\dfrac{1}{9}$ kg
(b) $\dfrac{1}{21}$ kg, $\dfrac{1}{9}$ kg
(c) $\dfrac{1}{21}$ kg, $\dfrac{1}{7}$ kg
(d) $\dfrac{1}{9}$ kg, $\dfrac{1}{7}$ kg
(e) $\dfrac{4800}{53}$ kg, $\dfrac{136000}{1463}$ kg

Answer 1

Hint: As the wooden box is similar to the cuboid therefore, we will apply the formula for the volume of the cuboid. The formula is given by length $\times $ breadth $\times $ height where the units will be according to the dimensions given in the question. We will use thickness t cm to find the internal dimensions of the box. Also, for finding the value 1 $c{{m}^{3}}$ unit we will use a unitary method in which we will divide the quantity of the whole object by its number.

Complete step-by-step answer:
Let us suppose that the rectangular wooden box is similar to the figure below.

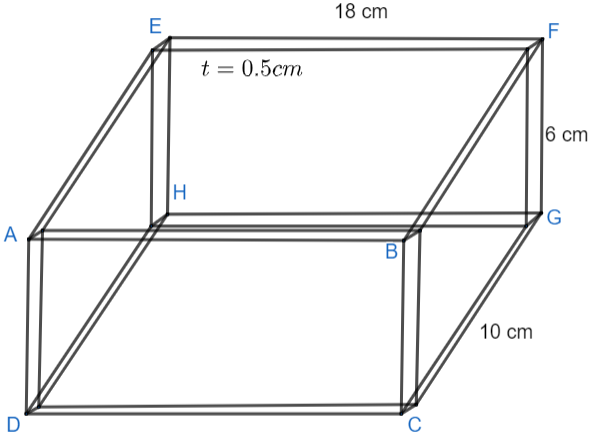
In this figure we can clearly see that the length of the box is 18 m while its breadth and height are 10 cm and 6 cm respectively. The thickness of the wooden board is denoted by t as $\dfrac{1}{2}$ cm or 0.5 cm. As we can clearly see that the box is empty, so now it is weighing 15 kg. But if sand is filled into it then its weight gets changed into 100 kg.
We are going to start the solution by finding out the external volume of the wooden box when it is empty. The external volume of the box will be similar to the cuboid which is given by length $\times $ breadth $\times $ height. By substituting the required dimensions into the formula we will get,
External volume of the wooden box = 18 cm $\times $ 10 cm $\times $ 6 cm
$\Rightarrow $ External volume of the wooden box = 180 $c{{m}^{2}}$ $\times $ 6 cm
$\Rightarrow $ External volume of the wooden box = 1080 $c{{m}^{3}}$
Thus, the external volume of the box when it is empty is 1080 $c{{m}^{3}}$. Now, as the thickness is 0.5 cm so, the length, breadth and height for the internal side of the box will be as,
The Internal length of the box will be 18 cm – 0.5 cm which results in 17.5 cm.
And the Internal breadth of the box will be 10 cm – 0.5 cm or we can say 9.5 cm.
Also, the internal height of the box is going to be 6 cm – 0.5 cm or 5.5 cm.
The required diagram for this is shown below.

Now, we will apply the formula of volume of cuboid again therefore, we get
The internal volume of the wooden box is 17.5 cm $\times $ 9.5 cm $\times $ 5.5 cm
$\Rightarrow $ External volume of the wooden box = 166.25 $c{{m}^{2}}$ $\times $ 5.5 cm
$\Rightarrow $ External volume of the wooden box = 914.375 $c{{m}^{3}}$
After this we will find the volume of the empty wooden box which is = external volume – internal volume of the box. Thus, we get that the volume of the box is 1080 $c{{m}^{3}}$ - 914.375 $c{{m}^{3}}$ which results into 165.625 $c{{m}^{3}}$. Now let us suppose that the sand is poured into the box. So, after this the volume of sand will be equal to the internal volume of the wooden box.
Thus, we get that the volume of the sand is 914.375 $c{{m}^{3}}$. According to the information in the question we have that the volume of the box (i.e., 165.625 $c{{m}^{3}}$) is 15 kg.
So, the weight of 1 $c{{m}^{3}}$ of wood will be $\dfrac{15}{165.625}$ kg. That is the weight is 0.090 $kg/c{{m}^{3}}$.
After filling up the box with sand the box will weigh 100 kg. So the weight of sand only will be 100 kg – 15 kg = 85 kg.
Also, as we know that the weight of 914.375 $c{{m}^{3}}$ of sand is 85 kg.
Therefore, the weight of 1 $c{{m}^{3}}$ of sand is $\dfrac{85}{914.375}$ kg. That is the weight is 0.093 $kg/c{{m}^{3}}$.
Hence, the correct option is (e).

Note: Always check the units of the dimensions. If they are the same then we will proceed otherwise we will first change them into the same unit and then move forward to the question. If in case the respected weights are asked in grams so, we will write 0.090 $kg/c{{m}^{3}}$ as 90 $g/c{{m}^{3}}$ and 0.093 $kg/c{{m}^{3}}$ as 93 $g/c{{m}^{3}}$ with the help of the conversion 1 kg = 1000 g. As the thickness is given to us that is why we have two dimensions one is external and other is internal if the wooden box. But if the thickness is not given to us then we will find the volume without external and internal dimensions. If the thickness is 1 cm then the correct option will be (b) $\dfrac{1}{21}$ kg, $\dfrac{1}{9}$ kg. If in case the thickness is taken wrong then, the answer will also get wrong. One should not get confused while performing calculations otherwise it will not lead to the right answer. Try solving with focus.