Question

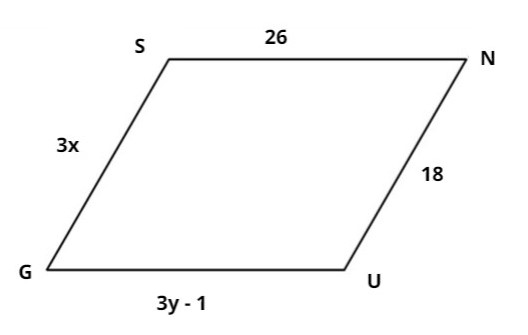
The following figure is a parallelogram. Find the length of \[(x + y)\] (length in centimeter).

Answer 1

Hint: The opposite sides of the parallelogram are always equal, Use this property of parallelogram to find the values of x and y separately and then add them to get the final result .
Compete Step by Step Solution:
We know that the opposite sides of a parallelogram are equal and it is also given that the lengths are centimeters. Therefore we need not worry about the conversion of units.
Now according to the figure given to us It is clear that
\[\begin{array}{l}
SN = 26\\
SG = 3x\\
GU = 3y - 1\\
NU = 18
\end{array}\]

According to the property of parallelogram
\[\begin{array}{l}
SG = NU\\
SN = GU
\end{array}\]
Now putting the values of these we will get it as
\[\begin{array}{l}
\therefore 3x = 18..............................(i)\\
\therefore 3y - 1 = 26...........................(ii)
\end{array}\]
On solving equation (i) we get
\[\begin{array}{l}
 \Rightarrow 3x = 18\\
 \Rightarrow x = \dfrac{{18}}{3}\\
 \Rightarrow x = 6
\end{array}\]
And for equation (ii) we will get it as
\[\begin{array}{l}
 \Rightarrow 3y - 1 = 26\\
 \Rightarrow 3y = 27\\
 \Rightarrow y = \dfrac{{27}}{3}\\
 \Rightarrow y = 9
\end{array}\]
 Now we are getting x and y as 6 and 9 respectively
\[\begin{array}{l}
\therefore x + y = 6 + 9\\
 \Rightarrow x + y = 15
\end{array}\]
Therefore the answer is 15 cm as in the question it was given that all the lengths are in centimeter only.

Note: Be careful while changing signs in solving equations. A minor mistake could lead to a completely different outcome and also note that the adjacent sides are equal in rhombus not in parallelogram.