Question

The formula to find the slant height of the cone is
A) $l = \sqrt {{h^2} - {r^2}} $
B) $l = \sqrt {{h^2} + {r^2}} $
C) $l = \sqrt {h + {r^{}}} $
D) $l = \sqrt {{h^{}} - r} $

Answer 1

Hint: Before writing the formula of slant height let us see what is slant height. The slant height of an object such as cone or pyramid is the distance along the curved surface drawn from the top to a point on the circumference of the circle at the base. In other words we can say that the slant height is the shortest possible distance from the base to the apex along the surface of the solid.

Complete step by step solution:
Let us first draw the image of the cone.

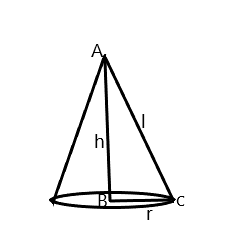
Here in the above image we have AC is the slant height i.e. $l$. AB is the vertical height of the cone $(h)$ and BC is the radius i.e. $r$.
Now the formula of the slant height of the cone is $l = \sqrt {{h^2} + {r^2}} $.
Hence the correct option is (B) $l = \sqrt {{h^2} + {r^2}} $.

Note:
Now we can apply this formula whenever we have to find the slant height of the cone. Let us take an example. The height and base of a cone is $8m$ and $12m$. Calculate its slant height. Now by applying the above formula we have $h = 8$ . We should note that we have a base which is diameter , so the radius is $\dfrac{d}{2} = \dfrac{{12}}{2} = 6$. So we have $r = 6$. Now by applying the formula we have $l = \sqrt {{8^2} + {6^2}} $. On solving we have $l = \sqrt {64 + 36} = \sqrt {100} $. It gives us a slant height of $10$.