Question

The interior of a building is in the form of a right circular cylinder of a diameter 4.2m and height 4 m, surmounted by a cone. The vertical height of the cone is 2.1m. Find the outer surface area and volume of the building. (Use π = 22/7)

Answer 1

Hint: Outer surface area of the building is the sum of Curved surface area of the cylinder and the curved surface area of the cone because the top and bases of the cylinder and cone are not considered as the outer parts of the building. Volume of the building is the sum of the volume of the cylinder and cone. Find the volumes and curved surface areas using the below mentioned formulas.
Formulas used:
Curved surface area and volume of a cylinder are $ 2\pi rh $ and $ \pi {r^2}h $ respectively, r is the radius and h is the height of the cylinder.
Curved surface area and volume of a cone are $ \pi rL $ and $ \dfrac{1}{3}\pi {r^2}h $ respectively, r is the radius, h is the height and L is the slant height of the cone.

Complete step-by-step answer:
We are given to find the outer surface area and volume of the building with base as a cylinder and a surmounted cone.

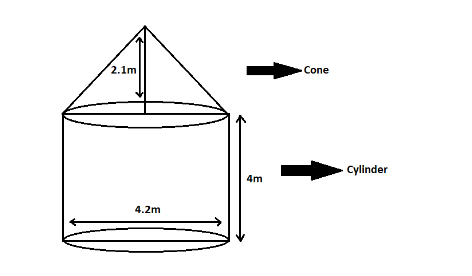
Radius is half the diameter; here the radius is half of 4.2m which is 2.1 m.
Outer surface area = Curved surface area of (Cylinder + Cone)
Curved surface area of the Cylinder is $ 2\pi rh $
 $ \Rightarrow CS{A_{cylinder}} = 2 \times \dfrac{{22}}{7} \times 2.1 \times 4 $
 $ \therefore CS{A_{cylinder}} = 52.8{m^2} $
To find the curved surface area of the cone, we need to find the length of its slant height.

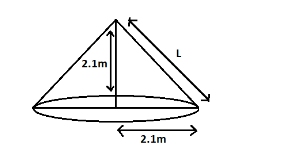
We can find the slant height using the Pythagoras theorem.
 $ L = \sqrt {{{2.1}^2} + {{2.1}^2}} = 2.1\sqrt 2 m $
Curved Surface area of the cone is
 $ \Rightarrow CS{A_{cone}} = \dfrac{{22}}{7} \times 2.1 \times 2.1\sqrt 2 = 19.6{m^2} $
Outer surface area of the building is $ 52.8 + 19.6 = 72.4{m^2} $
Next we have to find the volume of the building.
Volume of the cylinder is $ \pi {r^2}h $
$ Volum{e_{cylinder}} = \dfrac{{22}}{7} \times 2.1 \times 2.1 \times 4 = 55.44{m^3} $
Volume of the cone is $ \dfrac{1}{3}\pi {r^2}h $
$ Volum{e_{cone}} = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 2.1 \times 2.1 \times 2.1 = 9.702{m^3} $
 $\Rightarrow Volum{e_{building}} = Volum{e_{cylinder}} + Volum{e_{cone}} $
 $\therefore Volum{e_{building}} = 55.44 + 9.702 = 65.142{m^3} $
So, the correct answer is “$65.142{m^3} $”.

Note: Pythagoras theorem can be used only in right triangles, according to it, hypotenuse square is equal to the sum of the squares of its adjacent sides. And do not confuse vertical height with slant height in a cone. To solve this type of questions, we just need to know the formulas of their volumes and curved surface areas and if required total surface areas. Total surface area is different from curved surface area.