
The length of a focal chord of the parabola
A.
B.
C.
D.
Answer
493.5k+ views
Hint: We draw a rough figure for the situation where we have a parabola and a focal chord of length c. Using the property of vertically opposite angles we have the angle made by the chord with x-axis equal on both sides of the axis. With the help or right triangle formed by the shortest distance from the vertex to the chord we find cosecant of the angle. Substitute the value of cosecant of the angle in the formula for length of a chord.
* Focal chord is a chord that passes through the focus of the parabola
* In a right triangle having angle
*Length of focal chord of parabola
Complete step-by-step answer:
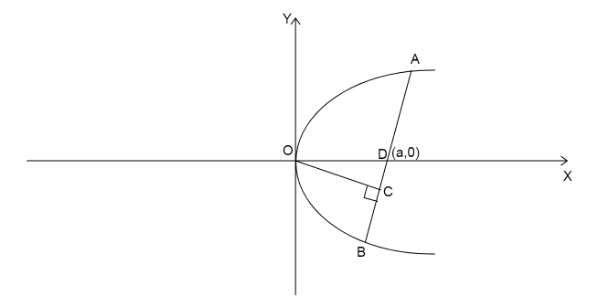
We are given a parabola
Let us assume that the chord cuts the X-axis at point D(a,0)
Then according to the question we are given the shortest distance from center to the chord is b.
Length of the focal chord is c.
The distance
Let us assume the focal chord makes an angle x with the X-axis.
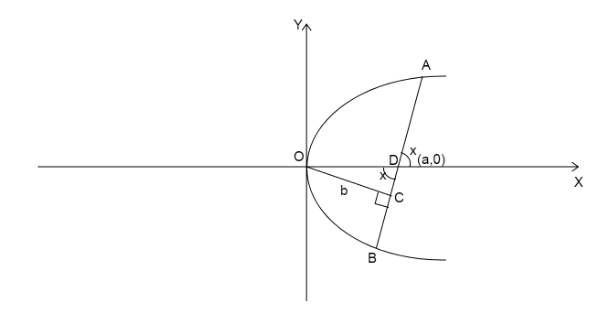
Since, we know vertically opposite angles are equal. Then,
Since, the shortest distance is the perpendicular distance, then
In right triangle OCD,
Substitute the value of OD as a and OC as b
Since we know
We know focal chord of a parabola
Therefore, we can write
Substitute the value of
Open the value on the bracket.
Cross multiply the value in denominator of RHS to LHS
Therefore, option D is correct.
Note: Students are likely to make the mistake of assuming the shortest distance as OD, which makes b equal to a. Keep in mind the shortest distance is the perpendicular distance and here the chord is not perpendicular to the x-axis so the perpendicular distance from vertex cannot be a.
* Focal chord is a chord that passes through the focus of the parabola
* In a right triangle having angle
*Length of focal chord of parabola
Complete step-by-step answer:

We are given a parabola
Let us assume that the chord cuts the X-axis at point D(a,0)
Then according to the question we are given the shortest distance from center to the chord is b.
Length of the focal chord is c.
The distance
Let us assume the focal chord makes an angle x with the X-axis.

Since, we know vertically opposite angles are equal. Then,
Since, the shortest distance is the perpendicular distance, then
In right triangle OCD,
Substitute the value of OD as a and OC as b
Since we know
We know focal chord of a parabola
Therefore, we can write
Substitute the value of
Open the value on the bracket.
Cross multiply the value in denominator of RHS to LHS
Therefore, option D is correct.
Note: Students are likely to make the mistake of assuming the shortest distance as OD, which makes b equal to a. Keep in mind the shortest distance is the perpendicular distance and here the chord is not perpendicular to the x-axis so the perpendicular distance from vertex cannot be a.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Franz thinks Will they make them sing in German even class 12 english CBSE




