
The length of an altitude of an equilateral triangle of side 2a is:-
A.
B.
C. 2 cm
D. 1 cm
Answer
481.2k+ views
Hint: For the solution of this question, we will be using the Pythagoras Theorem.
Pythagoras Theorem states that,
Now, since the triangle is an equilateral triangle, its altitude will bisect its base, and also, it will be perpendicular to its base.
So, as we get us Hypotenuse, Base and Perpendicular, we will put the values of Hypotenuse, Base and Perpendicular in the theorem to find the length of the altitude of the equilateral triangle.
The altitude will act like the perpendicular of the triangle which is equilateral.
Complete step by step answer:
Let the equilateral triangle be ABC.
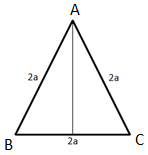
We will now draw the altitude AD,
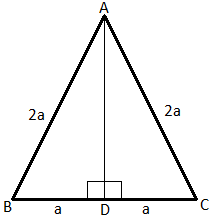
Now, in right angled ∆ABD, we will use the Pythagoras theorem as follows,
So, the measure of AD is
So, the correct answer is “Option B”.
Note: Let us now understand about Altitude and Median.
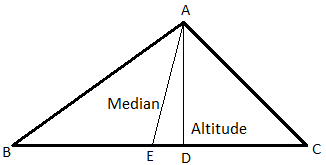
ALTITUDE: Altitude of a triangle is the perpendicular drawn from the vertex of the triangle to the opposite side. It is also known as the height of the triangle.
MEDIAN: A median of triangle is a line segment that joins a vertex to the mid-point of the side that is opposite to that vertex.
In the figure given below, in ∆ABC, AD is the altitude of the triangle ABC and AE is the median that divides BC into two equal halves, that is, BE = EC.
Pythagoras Theorem states that,
Now, since the triangle is an equilateral triangle, its altitude will bisect its base, and also, it will be perpendicular to its base.
So, as we get us Hypotenuse, Base and Perpendicular, we will put the values of Hypotenuse, Base and Perpendicular in the theorem to find the length of the altitude of the equilateral triangle.
The altitude will act like the perpendicular of the triangle which is equilateral.
Complete step by step answer:
Let the equilateral triangle be ABC.

We will now draw the altitude AD,

Now, in right angled ∆ABD, we will use the Pythagoras theorem as follows,
So, the measure of AD is
So, the correct answer is “Option B”.
Note: Let us now understand about Altitude and Median.
ALTITUDE: Altitude of a triangle is the perpendicular drawn from the vertex of the triangle to the opposite side. It is also known as the height of the triangle.
MEDIAN: A median of triangle is a line segment that joins a vertex to the mid-point of the side that is opposite to that vertex.
In the figure given below, in ∆ABC, AD is the altitude of the triangle ABC and AE is the median that divides BC into two equal halves, that is, BE = EC.

Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What is pollution? How many types of pollution? Define it




