
The magnifying power of the astronomical telescope for normal adjustment is 50. The focal length of the eyepiece is 2 cm. The required length of the telescope for normal adjustment is:
A. 100 cm
B. 98 cm
C. 25 cm
D. 102 cm
Answer
448.5k+ views
Hint: A telescope is an optical device used to look at distant objects like a star, a planet, or a distant tree etc. The magnification power of this telescope is given as $m = \dfrac{{ - {f_ \circ }}}{{{f_e}}}$ . And the length of telescope in normal adjustment i.e., when both object and image are at infinity is given by${f_u} + {f_e} = L$ .
$\eqalign{
& {\text{where }}m{\text{ is the magnification power of the telescope,}} \cr
& {f_ \circ }{\text{ is the focal length of the objective,}} \cr
& {f_e}{\text{ is the focal length of the eye piece,}} \cr
& L{\text{ is the length of the telescope for normal adjustment}}{\text{.}} \cr} $
Using the above-mentioned formulas we can solve the question, by substituting the given values and thus finding the required ones.
Complete step by step answer:
An astronomical telescope is a refracting type telescope used to see heavenly bodies like stars, planets, satellites, etc. It consists of two converging lenses mounted coaxially at the outer ends of two sliding tubes.
Magnifying power in the normal adjustment is defined as the ratio of the angle subtended at the eye by the final image as seen through the telescope to the angle subtended at the eye by the object seen directly when both image and object are at infinity.
Mathematically,
$m = \dfrac{{{f_ \circ }}}{{{f_e}}} \cdots \cdots \cdots \cdots \left( 1 \right)$
When the beam of light is incident on the objective, it forms a real, inverted, and diminished image of the object in its focal plane. The eyepiece is so adjusted that the image is formed at infinity, and is highly magnified and inverted with respect to the object. This setup is known as the normal adjustment.
For normal adjustment separation between object and image, i.e. the length of the telescope at normal adjustment is:
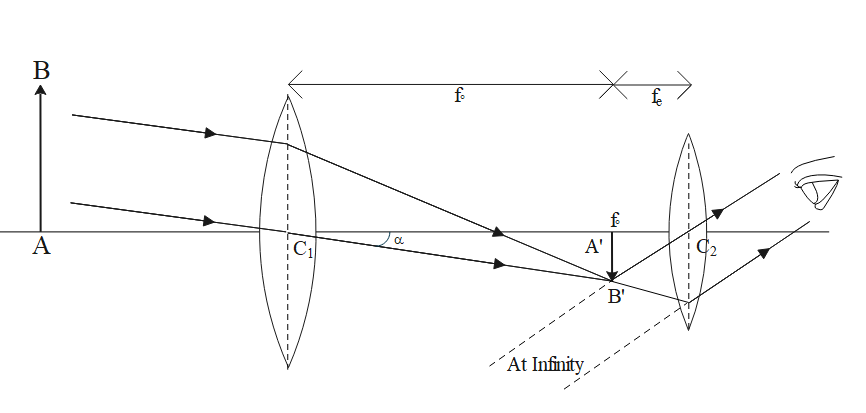
${f_ \circ } + {f_e} = L \cdots \cdots \cdots \cdots \left( 2 \right)$
Given:
m=50 and ${f_e} = 2cm$
Substituting the given values in equation (2) & (3) we get:
$\eqalign{
& {f_ \circ } + 2cm = L \cdots \cdots \cdots \left( 3 \right) \cr
& {\text{and }}50 = \dfrac{{{f_ \circ }}}{{{f_e}}} \cdots \cdots \cdots \cdots \left( 4 \right) \cr} $
Solving equation (4) we get:
$\eqalign{
& 50 = \dfrac{{{f_ \circ }}}{{{f_e}}} \cr
& \Rightarrow 50{f_e} = {f_ \circ } \cr
& {\text{But }}{f_e} = 2cm\left[ {given} \right] \cr
& \Rightarrow {f_ \circ } = 50 \times 2cm \cr
& \therefore {f_ \circ } = 100cm \cr} $
Substituting the calculated value of ${f_ \circ }$ in equation (3), we get:
$\eqalign{
& {f_ \circ } + 2cm = L \cr
& \Rightarrow 100cm + 2cm = L \cr
& \therefore L = 102cm \cr} $
Therefore, the correct option is D. i.e., 102cm
Note:
Students usually get confused a lot between the formula of the image formed at the distance of least distinct vision and in the normal adjustment. In order to rise above the confusion, they should associate the meaning of these system settings to the obtained result. For example at normal adjustment, both the image and the object are at infinity.
$\eqalign{
& {\text{where }}m{\text{ is the magnification power of the telescope,}} \cr
& {f_ \circ }{\text{ is the focal length of the objective,}} \cr
& {f_e}{\text{ is the focal length of the eye piece,}} \cr
& L{\text{ is the length of the telescope for normal adjustment}}{\text{.}} \cr} $
Using the above-mentioned formulas we can solve the question, by substituting the given values and thus finding the required ones.
Complete step by step answer:
An astronomical telescope is a refracting type telescope used to see heavenly bodies like stars, planets, satellites, etc. It consists of two converging lenses mounted coaxially at the outer ends of two sliding tubes.
Magnifying power in the normal adjustment is defined as the ratio of the angle subtended at the eye by the final image as seen through the telescope to the angle subtended at the eye by the object seen directly when both image and object are at infinity.
Mathematically,
$m = \dfrac{{{f_ \circ }}}{{{f_e}}} \cdots \cdots \cdots \cdots \left( 1 \right)$
When the beam of light is incident on the objective, it forms a real, inverted, and diminished image of the object in its focal plane. The eyepiece is so adjusted that the image is formed at infinity, and is highly magnified and inverted with respect to the object. This setup is known as the normal adjustment.
For normal adjustment separation between object and image, i.e. the length of the telescope at normal adjustment is:

${f_ \circ } + {f_e} = L \cdots \cdots \cdots \cdots \left( 2 \right)$
Given:
m=50 and ${f_e} = 2cm$
Substituting the given values in equation (2) & (3) we get:
$\eqalign{
& {f_ \circ } + 2cm = L \cdots \cdots \cdots \left( 3 \right) \cr
& {\text{and }}50 = \dfrac{{{f_ \circ }}}{{{f_e}}} \cdots \cdots \cdots \cdots \left( 4 \right) \cr} $
Solving equation (4) we get:
$\eqalign{
& 50 = \dfrac{{{f_ \circ }}}{{{f_e}}} \cr
& \Rightarrow 50{f_e} = {f_ \circ } \cr
& {\text{But }}{f_e} = 2cm\left[ {given} \right] \cr
& \Rightarrow {f_ \circ } = 50 \times 2cm \cr
& \therefore {f_ \circ } = 100cm \cr} $
Substituting the calculated value of ${f_ \circ }$ in equation (3), we get:
$\eqalign{
& {f_ \circ } + 2cm = L \cr
& \Rightarrow 100cm + 2cm = L \cr
& \therefore L = 102cm \cr} $
Therefore, the correct option is D. i.e., 102cm
Note:
Students usually get confused a lot between the formula of the image formed at the distance of least distinct vision and in the normal adjustment. In order to rise above the confusion, they should associate the meaning of these system settings to the obtained result. For example at normal adjustment, both the image and the object are at infinity.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

What is a transformer Explain the principle construction class 12 physics CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?




