Question

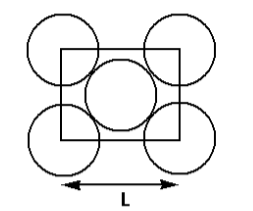
The packing efficiency of the two-dimensional square unit cell shown below is:

(A) $39.27\% $
(B) $68.02\% $
(C) $74.05\% $
(D) $78.54\% $

Answer 1

Hint: To solve this we must first calculate the total area occupied by the spheres in the unit cell and the total area of the square unit cell. The packing efficiency can then be calculated by the ratio of area of spheres in the unit cell to the total area of the square unit cell.

Complete step by step solution: Let the radius of each sphere or atom be r.
From the given diagram, we can conclude that the length of the diagonal of the square is ${\text{4}}r$. Thus,
$d = {\text{4}}r$ …… (1)
Where $d$ is the diagonal of the square,
$r$ is the radius of the sphere.
Let the side of the square be L.
We know the formula for the diagonal of the square is,
$d = \sqrt 2 \,a$
Where $d$ is the diagonal of the square,
$a$ is the side of the square.
Substitute L for the side of the square. Thus,
$d = \sqrt 2 \,L$ …… (2)
Equate equation (1) and equation (2). Thus,
$4r = \sqrt 2 \,L$
$L = \dfrac{{4r}}{{\sqrt 2 }}$ …… (3)
We know the formula for the area of the square is,
$A = {a^2}$
Where $A$ is the area of the square,
$a$ is the side of the square.
Substitute L for the side of the square. Thus,
$A = {L^2}$
Substitute $L = \dfrac{{4r}}{{\sqrt 2 }}$ from the equation (3). Thus,
$\Rightarrow A = {\left( {\dfrac{{4r}}{{\sqrt 2 }}} \right)^2}$
$\Rightarrow A = \dfrac{{16{r^2}}}{2}$
$\Rightarrow A = 8{r^2}$ …… (4)
From the diagram given, we can calculate that total number of spheres in one square unit. There is one sphere in the centre and there are four spheres at the four corners each contributing ${\text{1/4}}$ the area of its total area. Thus,
Total number of spheres $ = 1 + \left( {\dfrac{1}{4} \times 4} \right)$
Total number of spheres $ = 2$
We know the formula for the area of the sphere is,
$A = \pi {r^2}$
Where $A$ is the area of the sphere,
$r$ is the radius of the sphere.
As there are two spheres, the total area of the spheres is,
$A = 2\left( {\pi {r^2}} \right)$ …... (5)
The packing efficiency is the ratio of area of spheres in the unit cell to the total area of the square unit cell. Thus, to calculate the packing efficiency divide equation (5) by equation (4). Thus,
${\text{Packing efficiency}} = \dfrac{{2\left( {\pi {r^2}} \right)}}{{8{r^2}}}$
$\Rightarrow {\text{Packing efficiency}} = \dfrac{\pi }{4}$
Substitute $\pi = 3.14$. Thus,
$\Rightarrow {\text{Packing efficiency}} = \dfrac{{3.14}}{4}$
$\Rightarrow {\text{Packing efficiency}} = 0.7854$
Thus, the percentage packing efficiency is $0.7854 \times 100\% = 78.54\% $.
Thus, the packing efficiency of a two-dimensional square unit cell shown is $78.57\% $.

Thus, the correct option is (D) $78.54\% $.

Note: Here, we must carefully calculate the total number of spheres in the unit cell. The total number of spheres in the unit cell are two and not five. This is because the four spheres at the corner contribute one fourth of their total area each. This makes a total one sphere from the corners and one sphere at the centre. Thus, there are two spheres in the unit cell.