Question

The perimeter of a square field is 8 km. Find its area in hectares.

Answer 1

Hint: To solve the question given above, we will first find out what is a square. Then we will find the length of each side of the square using the information perimeter = 8 km given in the question. We will also use the known fact that perimeter is the sum of all side lengths of any shape. Then we will find the area of the square by the formula \[\text{Area }={{\left( \text{side} \right)}^{2}}.\] Now, we will convert this area from \[k{{m}^{2}}\] to hectares.

Complete step by step solution:
Before we solve this question, we must know what a square is. A square is a quadrilateral that has four sides which are equal in length and then the angle between each adjacent side pair is \[{{90}^{o}}.\] For a better understanding of the question, we will draw a rough sketch of a square.

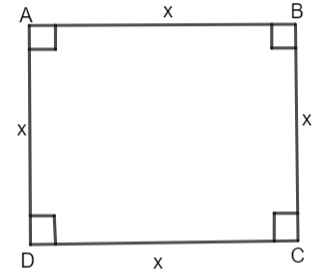
Now, we know that the length of each side of the square is the same, so we have assumed that the length of each side is x. Now, we will find the value of x. For this, we are given that the perimeter of the square is 8 km. The perimeter of any polygon is equal to the sum of the length of the sides of that polygon. Thus, we have the following equation.
Perimeter of square ABCD = AB + BC + CD + AD = 8 km
\[\Rightarrow x+x+x+x=8km\]
\[\Rightarrow 4x=8km\]
\[\Rightarrow x=2km\]
Thus, the length of each side of the square is 2 km.
Now, we will find the area of the square. The area of the square with the sides given is calculated by the formula, \[\text{Area of square }={{\left( \text{side} \right)}^{2}}.\]
Thus, we have,
\[\text{Area of square ABCD }={{\left( x \right)}^{2}}\]
\[\Rightarrow \text{Area of square ABCD }={{\left( 2km \right)}^{2}}\]
\[\Rightarrow \text{Area of square ABCD }=4k{{m}^{2}}\]
Now, we have to convert this area into hectares from \[k{{m}^{2}}.\] For this, we will use the following conversion.
\[1\text{ hectare}=0.01\text{ }k{{m}^{2}}\]
\[\Rightarrow 1\text{ }k{{m}^{2}}=100\text{ hectares}\]
Thus, we will have,
\[\Rightarrow \text{Area of square ABCD }=4\times 100\text{ hectares}\]
\[\Rightarrow \text{Area of square ABCD }=400\text{ hectares}\]

Note: We can also solve the given question by the following alternate method. We will divide the square into two right-angled triangles by making a diagonal as shown.

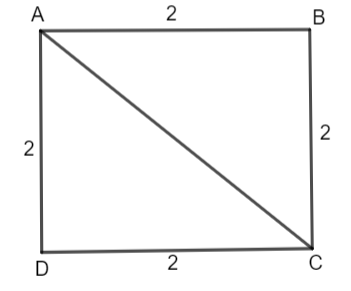
Now, the area of the square will be equal to twice the area of triangle ABC.
\[\text{Area of square ABCD}=2\times \text{ Area of }\Delta \text{ABC}\]
BC is the height of the triangle ABC and AB is the base. The area of a triangle with the given base and height is calculated by,
\[\text{Area }=\dfrac{1}{2}\times \text{base}\times \text{height}\]
Thus, we have,
\[\Rightarrow \text{Area of square ABCD}=2\times \left( \dfrac{1}{2}\times AB\times BC \right)\]
\[\Rightarrow \text{Area of square ABCD}=2\times \left( \dfrac{1}{2}\times 2\times 2 \right)\]
\[\Rightarrow \text{Area of square ABCD}=4k{{m}^{2}}\]