Question

The plan below shows the front wall of a warehouse. It is drawn on a scale of $1{\text{ cm}}$ to $2{\text{ m}}$. Based on this information answer the questions given below:

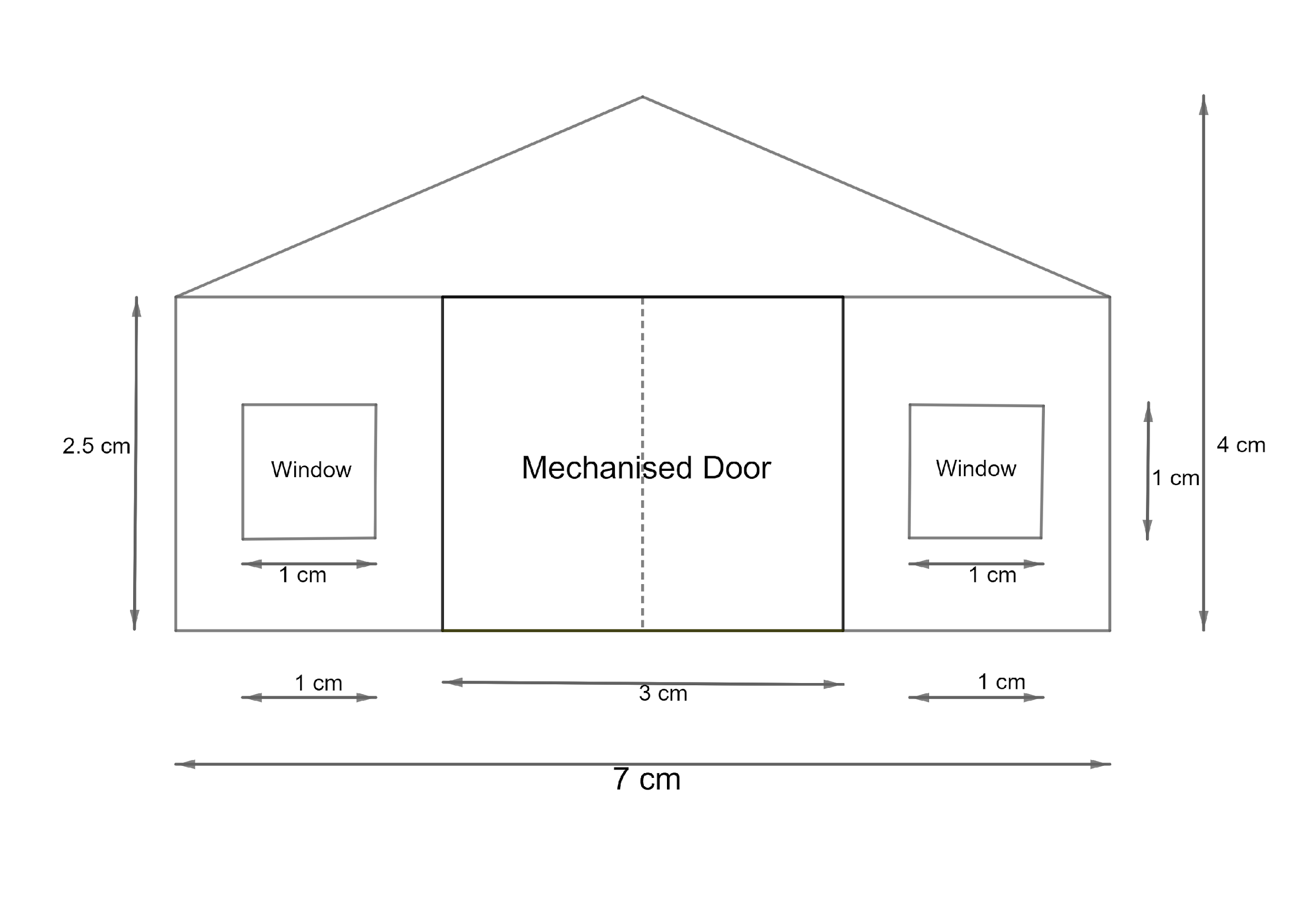
(i) What are the actual dimensions of the mechanised door?
(ii) What is the actual area taken up by the door and the windows?
(iii) Other than the windows and the door, the other part of the wall is cemented. Find the area of the cemented part.

Answer 1

Hint: The given question is related to scaling of models. A model is drawn of $1{\text{ cm}}$to $2{\text{ m}}$ First we will find the value of $k$which is the factor of scaling . It is found by dividing the original length by the model length. Then note that the lengths of the model are directly proportional to $k$, where as for the area of the model it is directly proportional to ${k^2}$. So say for a factor $2$, the length of the model is $2cm$ then length will be given by $2 \times 2$. But if area of the model is $2$ then the original area will be $2 \times {2^2} = 8$

Complete step by step answer:
The scaling factor $k$ will be given by,
$k = \dfrac{{200}}{1}$
$1 cm \to 2m $
$1 cm \to 200 cm$
It implies that the scaling factor is $200$.
so $k = 200$

(i) The dimensions of the door in the plan is $3 \times 2.5{\text{ }}cm$. The whole dimensions will be multiplied by the factor $k$ which we calculated as $200$.
So the dimensions are
$(3 \times 200) \times (2.5 \times 200)$
$600{\text{ cm }} \times {\text{ 500 cm}}$
$6{\text{ m }} \times {\text{5 m}}$
Therefore, the actual dimensions of the mechanised door is $ 6m \times 5m$.

(ii) The area of doors and windows in the plan will be calculated then multiplied by ${k^2} = 40000$. Both the windows and the door are rectangles.
The area of door $= 3 \times 2.5$
$ \Rightarrow 7.5{\text{ }}c{m^2}$
Area of two windows$ =2\left( {1 \times 1} \right)$
$ \Rightarrow 2{\text{ }}c{m^2}$
Total Area of doors and windows in the plan:
$ \Rightarrow 7 + 2.5 = 9.5{\text{ }}c{m^2}$
Total area of doors and windows in model$ = 9.5 \times 40000$
$ \Rightarrow 380000{\text{ c}}{{\text{m}}^2}$
$ \Rightarrow $$38{\text{ }}{m^2}$
Therefore, the actual area taken up by the door and the windows $38{\text{ }}{m^2}$.

(iii) We will find the total area of the wall and then subtract the area of doors and windows we calculated,
The Total Area of Wall will be equal to the area of the bottom rectangle and the upper triangle.
The area of rectangle $ =7 \times 2.5{\text{ c}}{{\text{m}}^2}$
$ \Rightarrow 17.5{\text{ }}c{m^2}$
The area of triangle will be :
$A = \dfrac{1}{2} \times Base \times Altitude$
$A = \dfrac{1}{2} \times 7 \times 1.5$
$A = 5.25 cm^2$
Total Area=$17.5 + 5.25 = 22.75$
$\text{Total Area - Area of door and Area of two windows} =22.75-9.5 cm^2 $
$=13.25 cm^2$
The area in real life =$13.25 \times 40000$
$530000{\text{ c}}{{\text{m}}^2}$
$ \Rightarrow 53{\text{ }}{{\text{m}}^2}$
The area of the cemented part is $53m^2$.

Note:
We could also have solved the above question without using the scaling factor method for area conversion. We would have expressed each dimension in the model to the dimension in real life and then calculated the subsequent areas of the figures.