Question

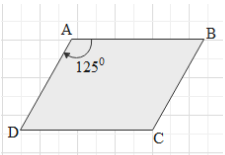
The rhombus is not drawn to scale. Find the other three angles of the given rhombus.

Answer 1

Hint:A rhombus is a special type of quadrilateral, whose both pairs of opposite sides are parallel and all the four sides are equal in lengths. The opposites angles of a rhombus are equal and the both the diagonals bisect each other.

Complete step by step answer:
Let us first understand what a rhombus is. A four sided convex polygon is called quadrilateral. A rhombus is a special type of quadrilateral, whose both pairs of opposite sides are parallel and all the four sides are equal in lengths. We can observe these properties in the figure given in the question.

Let us discuss the other properties of a rhombus.The opposites angles of a rhombus are equal and the both the diagonals bisect each other. We now know that the opposite angles of a rhombus are equal. Therefore, the angle C is equal to angle A and angle B is equal to angle D.
i.e. $\angle A=\angle C$ and $\angle B=\angle D$.
It is given that $\angle A={{125}^{\circ }}$.
This means that $\angle C=\angle A={{125}^{\circ }}$.

To find the other two angles of the rhombus, we shall use the property of a quadrilateral that the sum of all (four) the interior angles is equal ${{360}^{\circ }}$.
This means that $\angle A+\angle B+\angle C+\angle D={{360}^{\circ }}$.
Substitute the values of the angles A and C.
$\Rightarrow {{125}^{\circ }}+\angle B+{{125}^{\circ }}+\angle D={{360}^{\circ }}$
$\Rightarrow \angle B+\angle D={{360}^{\circ }}-{{250}^{\circ }}={{110}^{\circ }}$

But we know that $\angle B=\angle D$. Therefore, substitute $\angle B=\angle D$ on the above equation.
$\Rightarrow \angle D+\angle D={{110}^{\circ }}$
$\Rightarrow \angle D={{55}^{\circ }}$
$\therefore \angle B={{55}^{\circ }}$.

Therefore, the other three angles of the rhombus are ${{55}^{\circ }}$, ${{125}^{\circ }}$ and ${{55}^{\circ }}$.

Note:Actually, a rhombus is a special type of parallelogram. A parallelogram is a quadrilateral whose both pairs of opposite sides are parallel and equal in lengths.A rhombus becomes a square when all the four angles of the rhombus are equal to ${{90}^{\circ }}$.Note that a square is a rhombus but a rhombus is not a square.