Question

The sides of a triangle are 5 cm, 12 cm and 13 cm, then its area is
A.\[0.0024{m^2}\]
B.\[0.0026{m^2}\]
C.\[0.003{m^2}\]
D.\[0.0015{m^2}\]

Answer 1

Hint: Here we have to find the area of the triangle whose three sides are given. Before finding the area, we will check whether the triangle is a right angled triangle or not by using Pythagora's theorem. Then we will directly apply the formula of area for the right angled triangle. From there, we will get the area of the required triangle.

Formula used:
We will use the formula for the area of the triangle ,\[\dfrac{1}{2} \times b \times h\] , where \[b\] is the base and \[h\]is the height of the triangle.

Complete step-by-step answer:
The given sides of a triangle are 5 cm, 12 cm and 13 cm.
We will draw the triangle using the given measurement.

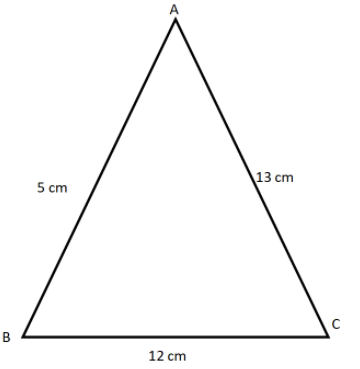
We have to find the area of the triangle here, but we will first check whether the given triangle is Pythagoras or not.
We know the Pythagoras theorem states the square of the hypotenuse is equal to the sum of the squares of the other two sides of a triangle.
Therefore, applying the theorem, we get
\[ \Rightarrow {13^2} = {5^2} + {12^2}\]
Finding the squares of the numbers, we get
\[ \Rightarrow 169 = 25 + 144\]
On adding numbers, we get
\[ \Rightarrow 169 = 169\]
It is satisfying the Pythagoras theorem, thus the given triangle is a right-angled triangle.
Thus, the hypotenuse is 13 cm, base is 5 cm and height is 2 cm.
Now, we will calculate the area of this right angled triangle.
We will substitute the value of base and height of the triangle.
\[ \Rightarrow {\rm{Area}} = \dfrac{1}{2} \times 5 \times 12\]
Multiplying the numbers, we get
\[ \Rightarrow {\rm{Area}} = 30c{m^2}\]
But, we need an area in\[{m^2}\].
We know, \[1cm = \dfrac{1}{{100}}m\]
Thus, \[1c{m^2} = \dfrac{1}{{10000}}{m^2}\]
Therefore, area becomes;
\[ \Rightarrow {\rm{Area}} = 30 \times \dfrac{1}{{10000}}{m^2} = 0.003{m^2}\]
Hence, the correct option is C.

Note: Triangle is a two-dimensional closed geometric shape that has three sides. There are different types of the triangle and they are equilateral triangle, isosceles triangle, right-angled triangle, etc. If the sides of any triangle satisfy the Pythagoras theorem, then that triangle will be a right-angled triangle. We can use Pythagoras theorem in right-angled triangles only. A right-angled triangle is that triangle whose one of the angles is equal to \[90^\circ \].