Question

The slant height of the frustum of a cone is 4cm, and the perimeter of its circular bases are 18cm and 6cm. Find the curved surface area of the frustum of a cone.

Answer 1

Hint: Hint: For the above question we will use the formula of the curved surface area of the frustum of a cone having smaller radius ‘r’, bigger radius ‘R’ and slant height ‘l’ is given by as follows:
$curved\ surface\ area=\pi \times l\times \left( R+r \right)$
We also know that the perimeter of the circular base is the circumference of the circle, given by $2\pi r$. Using this, we can find the respective radius.

Complete step-by-step solution
We have been given the slant height of the frustum of a cone is 4cm and the perimeter of its smaller and bigger circular bases are 6cm and 18cm respectively and we have been asked to find its curved surface area.

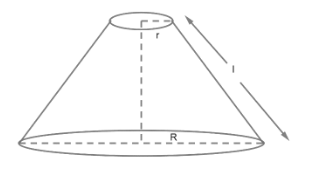
Let us suppose the slant height of frustum to be l and radius of smaller and bigger circular bases are r and R respectively. We know that $curved\ surface\ area=\pi \times l\times \left( R+r \right)$.
We have, $l=4cm,2\pi r=6cm\ and\ 2\pi R=18cm$.
Since, we know that the perimeter of a circular base having radius a unit is equal to $\left( 2\pi a \right)$.
$\begin{align}
  & \Rightarrow 2\pi r=6 \\
 & \Rightarrow \pi r=3 \\
 & \Rightarrow r=\dfrac{3}{\pi } \\
 & Also,\ 2\pi R=18 \\
 & \Rightarrow \pi R=9 \\
 & \Rightarrow R=\dfrac{9}{\pi } \\
\end{align}$
So, curved surface area \[=\pi \times 4\times \left( \dfrac{9}{\pi }+\dfrac{3}{\pi } \right)\]
 \[\begin{align}
  & =\pi \times 4\times \left( \dfrac{9+3}{\pi } \right) \\
 & =\pi \times 4\times \dfrac{12}{\pi } \\
 & =48cm \\
\end{align}\]
Therefore, the curved surface area of frustum of a cone is equal to 48cm.

Note: It is better to not calculate the exact value of r and R by substituting the value of $'\pi '$ as it will become more complex and also we will get an approximate value for curved surface area after that.Also, remember that we have been given perimeter of the circular bases but sometimes by mistakes we treat it like radius and we substitute the values in the formula which give us a wrong answer. So, be careful at that time.