Question

The total surface area of a cylinder is 462 ${\text{c}}{{\text{m}}^2}$and its curved surface area is $\dfrac{1}{3}$​ of its total surface area. Find the radius of the cylinder (in cm).

Answer 1

Hint: In order to solve this problem, we must use the concept that the total surface area is the sum of curved surface area with upper and bottom cross sections areas.

Complete step-by-step answer:

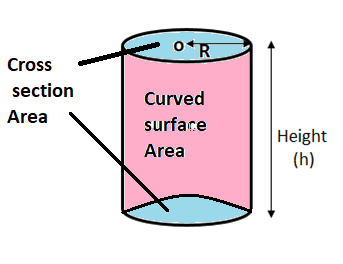
The total surface area of a cylinder is 462 ${\text{c}}{{\text{m}}^2}$and its curved surface area is $\dfrac{1}{3}$​ of its total surface area
So curved surface area we can find with help of given total surface area
So curved surface area = $\dfrac{1}{3}$ ×( total surface area of a cylinder)
$\therefore $ curved surface area = $\dfrac{1}{3}$ ×( 462)
On solving
$\therefore $ curved surface area = 154 ${\text{c}}{{\text{m}}^2}$ (1)

With the reference of figure,
We can say that the total surface area is a summation of the curved surface area along with the upper and bottom cross section area.

Hence we can write
Total surface area of cylinder = curved surface area + upper cross section area + bottom cross section area …… (2)
We know that
 upper cross section area = bottom cross section area = $\pi {{\text{r}}^2}$
Total surface area of a cylinder is 462 ${\text{c}}{{\text{m}}^2}$ (given in question)
Put the value of curved surface area from equation (1)
So on putting all the values in result (2)
Total surface area = curved surface area + upper cross section area + bottom cross section area
⇒462 ${\text{c}}{{\text{m}}^2}$= 154 ${\text{c}}{{\text{m}}^2}$+ $\pi {{\text{r}}^2}$+ $\pi {{\text{r}}^2}$
⇒462 ${\text{c}}{{\text{m}}^2}$= 154 ${\text{c}}{{\text{m}}^2}$+ 2$\pi {{\text{r}}^2}$
⇒308 = 2$\pi {{\text{r}}^2}$
On putting $\pi = \dfrac{{22}}{7}$
⇒$2 \times \dfrac{{22}}{7} \times {{\text{r}}^2} = 308$

$ \Rightarrow {{\text{r}}^2} = \dfrac{{308 \times 7}}{{44}}$
On solving
$ \Rightarrow {{\text{r}}^2} = 49$
Taking square root on both side
$ \Rightarrow \sqrt {{{\text{r}}^2}} = \sqrt {49} $
$ \Rightarrow {\text{r}} = 7$ cm

Hence the required radius of cylinder is r=7 cm.

Note: Whenever we face such types of problems the point is to have the good gist of the diagrammatic representation using the information provided in the question as it helps understanding the geometry of the figure involved. It is always advisable to learn the direct formula for some of the basic conic sections like the cylinder as it helps and saves a lot of time.