Question

What should be the value of the $R$ so that the electric power consumed by it is maximum:

 $ \left( A \right)12\Omega $
 $ \left( B \right)24\Omega $
 $ \left( C \right)6\Omega $
 $ \left( D \right)$ None of the above

Answer 1

Hint: From the figure we can say that the four resistance that is $ 5\Omega ,20\Omega ,10\Omega \,{\text{and}}\,40\Omega $ are connected in the principle of Wheatstone bridge.
The Wheatstone’s bridge: works on the principle that where the ratio of the resistances is equal, no current flows through the galvanometer which is connected in the middle of the circuit.
Now from that we can say that the $ 12\Omega $ resistance shows no current flow through it and it is open circuited. Now using the maximum power theorem we can find the value resistance $R$.
Maximum power transfer theorem (for DC circuits) states that the power transferred to the load is maximum when the load resistance is equal to source resistance.

Complete step by step answer:
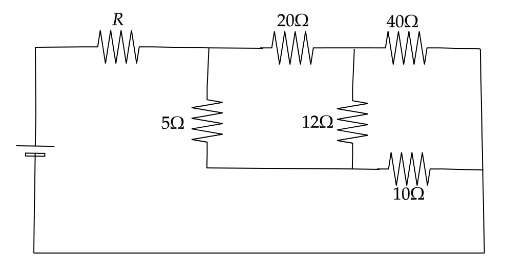
Let’s observe the Wheatstone bridge circuit in the given image. This can be seen in the below image.

Now using Wheatstone bridge principle we can say that,
 $ \dfrac{{20\Omega }}{{5\Omega }} = \dfrac{{40\Omega }}{{10\Omega }} $
Hence from this we can say that the current does not flow through the $ 12\Omega $ will be zero and it acts as an open circuit.
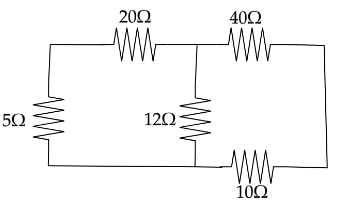
Now the circuit will look like we will get,

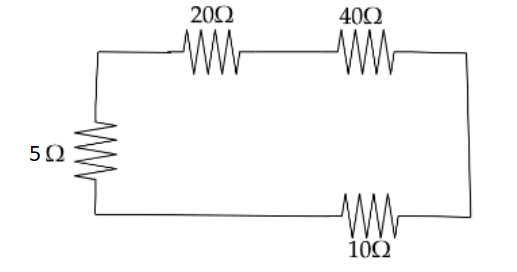
Where $ 20\Omega $ and $ 40\Omega $ were connected in series and resistances $ 5\Omega $ and $ 10\Omega $ are connected in series then after it will be connected in parallel.

Now the equivalent resistance will be,
 $ {R_{{\text{eq}}}} = {R_{60}}||{R_{15}} = \dfrac{{{R_{60}} \times {R_{15}}}}{{{R_{60}} + {R_{15}}}} $
Now putting the given values we will get,
 $ {R_{{\text{eq}}}} = \dfrac{{60 \times 15}}{{60 + 15}}\Omega = 12\Omega $
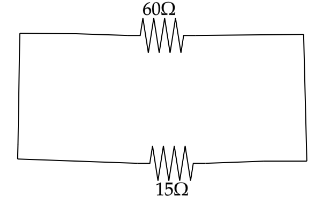
Now put circuit will look like,

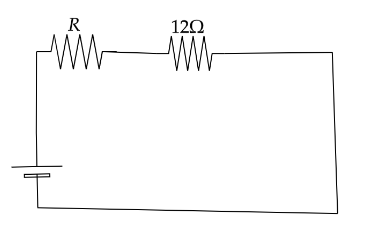
Now using maximum power transfer theorem we can say that, Source resistance is equal to load resistance.
$ R = {R_L} $
Where,
$ {R_L} $ is the load resistance where the load resistance value is equal to $ 12\Omega $ .
Now we can say that the value of resistance $R$ in the circuit is $ 12\Omega $.
Therefore, the value of $R= 12 \Omega $ option (A) is correct..

Note:
Remember that the maximum power transform states that to obtain maximum external power from a source in a circuit with finite internal resistance where the resistance of the load must be equal to the resistance of the source as viewed from its output terminal.