Question

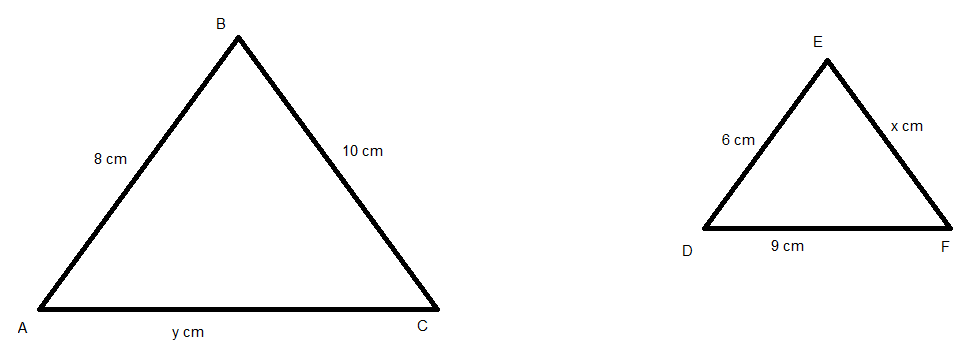
Triangle ABC is similar to triangle DEF.
Calculate the value of
a). \[x\],
b). \[y\]

Answer 1

Hint: To solve this question we have given two similar triangles then we use the concept of a similar triangle that is the ratio of all sides of the triangle to all sides of a triangle are equal. Then equate that with the constant term and from there we are able to find the length of all unknown sides.

Complete step-by-step solution:
Given,
Two similar figures are given with all the known sides in terms of variables.
To find,
All the variables that are used in two figures.
These two figures are similar given in question. Then we use the side, side, side rule which says that ratios of all sides of the triangle to the all sides of another triangle.
\[\Delta ABC \approx \Delta DEF\] (given)
Then the ratios of all the sides are equal
\[\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}} = \dfrac{{AC}}{{DF}}\]
On putting all these values from the diagram.
\[\dfrac{9}{6} = \dfrac{{10}}{x} = \dfrac{y}{9}\]
Now, equating first two terms in order to get the value of \[x\]
\[\dfrac{9}{6} = \dfrac{{10}}{x}\]
On arranging
\[9 \times x = 10 \times 6\]
On simplifying
\[9x = 60\]
On further solving
\[x = \dfrac{{60}}{9}\]
The value of \[x\] in the given triangle is
\[ \Rightarrow x = \dfrac{{60}}{9}\]
Now comparing first and third term in order to get the value of \[y\]
\[\dfrac{9}{6} = \dfrac{y}{9}\]
On rearranging
\[9 \times 9 = y \times 6\]
Of simplifying
\[\dfrac{{81}}{6} = y\]
The value of side y is
\[y = \dfrac{{81}}{6}\]
Final answer:
The value of \[x\] in the given triangle is
\[ \Rightarrow x = \dfrac{{60}}{9}\]
The value of side y is the given triangle is
\[y = \dfrac{{81}}{6}\]

Note: If a figure is large and a new fig is formed smaller to that then smaller in the sense that all dimensions are reduced in a fixed proportion. Other than the side, side, side rule many rules exist to prove similar triangles. The rules are the side, angle, side (SAS) rule, and angle, angle, angle (AAA) rule. This is used to prove the similarity of triangles. In similar figures like triangle sides are to be in the same ratio.