Question

Two spherical conductors A and B of radii $1mm$ and $2mm$ separated by a distance of $5cm$ and are uniformly charged. IF the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is:

Answer 1

Hint: In the equilibrium condition, the potential at the surface of both the sphere would be the same and hence, by equating them we can find out the total charge on each sphere. From the values of the charge, we can find out the electric fields at the surface of the two spheres.
Formula used:
$V=K\dfrac{Q}{R}$
$E=K\dfrac{Q}{{{R}^{2}}}$

Complete answer:
 In the equilibrium condition, the potential of both the spherical conductors will be equal and hence, we will use the formula for the potential on a spherical conductor at its surface in terms of the charge on the sphere and its radius.

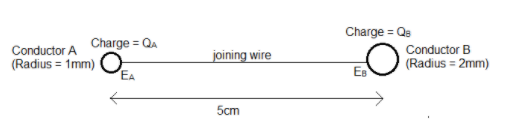
The potential $V$ at the surface of a spherical conductor of radius $R$ and total charge $Q$ is given by
$V=K\dfrac{Q}{R}$ --(1)
where $K=9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}$ is the universal electric constant.
Also, the electric field $E$ on the surface of a uniformly charged spherical conductor having charge $Q$ and radius $R$ is given by
$E=K\dfrac{Q}{{{R}^{2}}}$ --(2)
Now, let us analyze the question.
The radius of the sphere A is ${{R}_{A}}=1mm$
Let the charge on the sphere A be ${{Q}_{A}}$
Let the electric field on the surface of sphere $A$ be ${{E}_{A}}$
Let the potential at the surface of sphere $A$ be ${{V}_{A}}$.
The radius of the sphere B is ${{R}_{B}}=2mm$
Let the charge on the sphere B be ${{Q}_{B}}$
Let the electric field on the surface of sphere $B$ be ${{E}_{B}}$
Let the potential at the surface of sphere $B$ be ${{V}_{B}}$.
Now since the two spheres are joined by a wire and they are in equilibrium, their potentials must be the same.
$\therefore {{V}_{A}}={{V}_{B}}$ --(3)
Also, using (1), we get
${{V}_{A}}=K\dfrac{{{Q}_{A}}}{{{R}_{A}}}$ --(4)
${{V}_{B}}=K\dfrac{{{Q}_{B}}}{{{R}_{B}}}$ --(5)
Putting (4) and (5) in (3), we get
$K\dfrac{{{Q}_{A}}}{{{R}_{A}}}=K\dfrac{{{Q}_{B}}}{{{R}_{B}}}$
$\therefore \dfrac{{{Q}_{A}}}{{{R}_{A}}}=\dfrac{{{Q}_{B}}}{{{R}_{B}}}$
$\therefore \dfrac{{{Q}_{A}}}{{{Q}_{B}}}=\dfrac{{{R}_{A}}}{{{R}_{B}}}$ --(6)
Now, using (2), we get
${{E}_{A}}=K\dfrac{{{Q}_{A}}}{{{R}_{A}}^{2}}$
${{E}_{B}}=K\dfrac{{{Q}_{B}}}{{{R}_{{{B}^{2}}}}}$
$\therefore \dfrac{{{E}_{A}}}{{{E}_{B}}}=\dfrac{\dfrac{{{Q}_{A}}}{{{R}_{A}}^{2}}}{\dfrac{{{Q}_{B}}}{{{R}_{B}}^{2}}}=\dfrac{{{Q}_{A}}}{{{Q}_{B}}}{{\left( \dfrac{{{R}_{B}}}{{{R}_{A}}} \right)}^{2}}$ --(7)
Putting (6) in (7), we get
$\dfrac{{{E}_{A}}}{{{E}_{B}}}=\dfrac{{{R}_{A}}}{{{R}_{B}}}{{\left( \dfrac{{{R}_{B}}}{{{R}_{A}}} \right)}^{2}}=\dfrac{{{R}_{B}}}{{{R}_{A}}}=\dfrac{2}{1}=2:1$
Therefore, we have got the required ratio of the magnitudes of the electric field at the surfaces of the two spherical conductors as $2:1$.

Note:
Students must note that in this problem, we ignored the effect of the second spherical conductor on the first and the electric field at the surface of the second sphere due to the first because the distance between the spheres was much greater than the radii of the spheres and since the magnitude of the electric field falls off as the square of the distance, so in effect the electric field due to a second sphere at the first sphere would not have any considerable effect. However, if the distance between the spheres would be comparable to their radii, then we would have taken into account the other sphere’s contribution also while calculating the electric field at the surface of one of the spheres.