Question

How do you use area models to divide $ 640 \div 21 $ ?

Answer 1

Hint: Area model is a rectangular diagram or model used for multiplication and division problems, in which the quotient and divisor define the length and breadth of the rectangle and dividend define the area of the rectangle.
First, we draw a box and write the dividend inside the box, and the divisor on the left side.
On top of the rectangle, we estimate the quotient such that the product of divisor and quotient is not greater than the dividend.
The product obtained is subtracted from dividend and the difference is the remainder.
If the remainder is less than the divisor then we stop. Else we will take another rectangle of same length for the remaining remainder and follow the same steps till we get the remainder less than divisor.

Complete step-by-step answer:
Let us take a rectangle and consider $ 640 $ as its area and $ 21 $ as its length. Now we write the area inside the rectangle and length to the left of the rectangle.

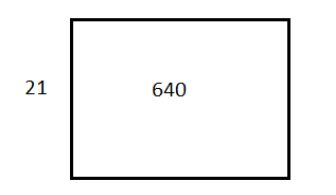
Let us estimate the breadth for the rectangle such that the breadth times the length ( $ 21 $ in this case) is not greater than the area of the rectangle.
Write this estimate above the rectangle.
In this case let us estimate that breadth is $ 30 $

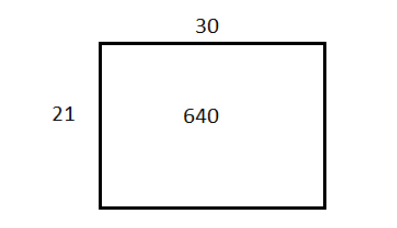
Multiply this length and estimated breadth and then subtract their product from the area of the rectangle.

The remainder we got is the remaining area. Since the remainder is less than the length of the rectangle we will stop at this point.
Hence the answer is $ 30\dfrac{{10}}{{21}} $ or $ 30R10 $
If the remainder was greater than the length, we will continue the steps by taking another rectangle of the same length for the remaining area.

Note: Suppose if we had taken the initial estimate of breadth as $ 20 $ .
Multiplying this estimate times the length and subtracting the product we get,

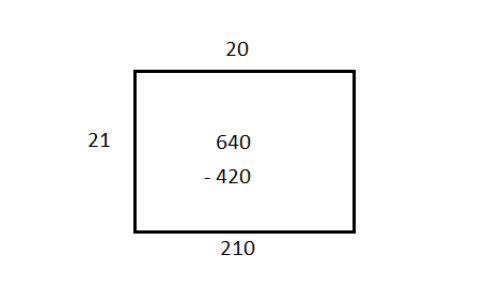
We still have an area of $ 210 $ so we will draw another rectangle of the same length beside the existing rectangle and write the excess area inside the new rectangle.

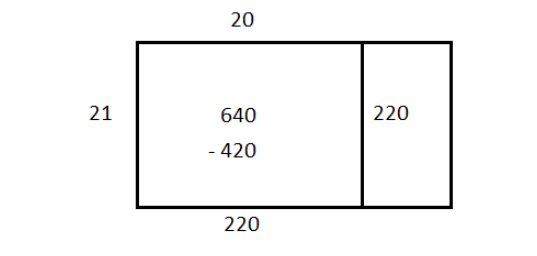
Again we will estimate the breadth of this excess area and repeat the process

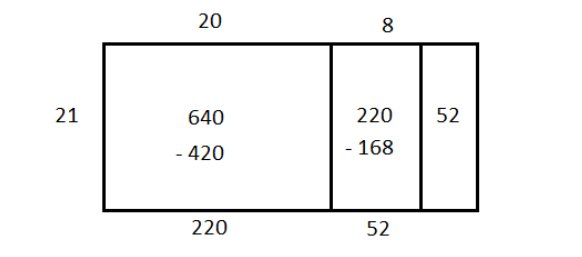
Since the excess area is still greater than the length of the rectangle,
we write this new excess area in another rectangle and repeat.

Now the excess area is less than the length and we can no longer continue.
The breadth of the series of rectangles is $ 20 + 8 + 2 = 30 $ with a remainder of $ 10 $ .
This is the same as the above answer.
It is very important to estimate the proper number such that the division process becomes easier.