Easy NCERT Exemplar for Class 10 Maths Chapter 10 - Constructions (Book Solutions)

EXERCISE 10.1

1. To divide a line segment  $AB$  in the ratio $5:7$, first, a ray  $AX$  is drawn so that  $\angle BAX$  is an acute angle and then at equal distances points are marked on the ray  $AX$  such that the minimum number of these points is

(A)  $8$ 

(B)  $40$ 

(C)  $41$ 

(D)  $42$  

Correct Answer: D

Ans:  Since, to divide a line segment ${\text{AB}}$  in the ratio $ m : n $ , first draw a ray  $AX$ which makes an acute angle $\angle BAX$ , then marked  ${\text{m  +  n}}$  points at equal distance on ${\text{AX}}$ . 

Here,  $m = 5,n = 7$  

So, minimum number of these points  $= m + n = 5 + 7 = 12$ 

2. To divide a line segment  $AB$  in the ratio $4:7$ , a ray  $AX$  is drawn first such that  $\angle BAX$  is an acute angle and then points  ${A_1},{A_2},{A_3}, \ldots . $  are located at equal distances on the ray  $AX$  and the point  $ B $  is joined to

(A)  ${A_{12}}$ 

(B)  ${A_{11}}$ 

(C)  ${A_{10}}$ 

(D)  ${A_{12}}$  

Correct Answer: B

Ans: To divide a line segment ${\text{AB}}$  in the ratio  $ m : n $ , first draw a ray  $AX$ which makes an acute angle  $\angle BAX$ , then marked  $ m  +  n $  points at equal distance on  $AX$ . 

Here, minimum  $4 + 7 = 11$  points are located at equal distances on the raY$AX$ , and then  $ B $  is joined to last point ${A_{11}}$ .

3. To divide a line segment  $AB$  in the ratio  $5:6$ , draw a ray  $AX$  such that  $\angle BAX$  is an acute angle, then draw a ray  $ BY$  parallel to  $AX$  and the points  ${A_1},{A_2},{A_3}, \ldots  $  and  ${B_1},{B_2},{B_3}, \ldots  $  are located at equal distances on ray  $AX$  and  $ BY$ , respectively. 

Then the points joined are

(A) ${A_5}$  and  ${B_6}$ 

(B)  ${A_6}$  and  ${B_5}$ 

(C)  ${A_4}$  and  ${B_5}$ 

(D)  ${A_5}$  and  ${B_4}$  

Correct Answer: A

Ans: Step 1: Draw a ray  $AX$  making an acute $\angle BAX$.

Step 2: Draw a ray  $ BY$  parallel to  $AX$  by making  $\angle ABY$  equal to $\angle BAX$.

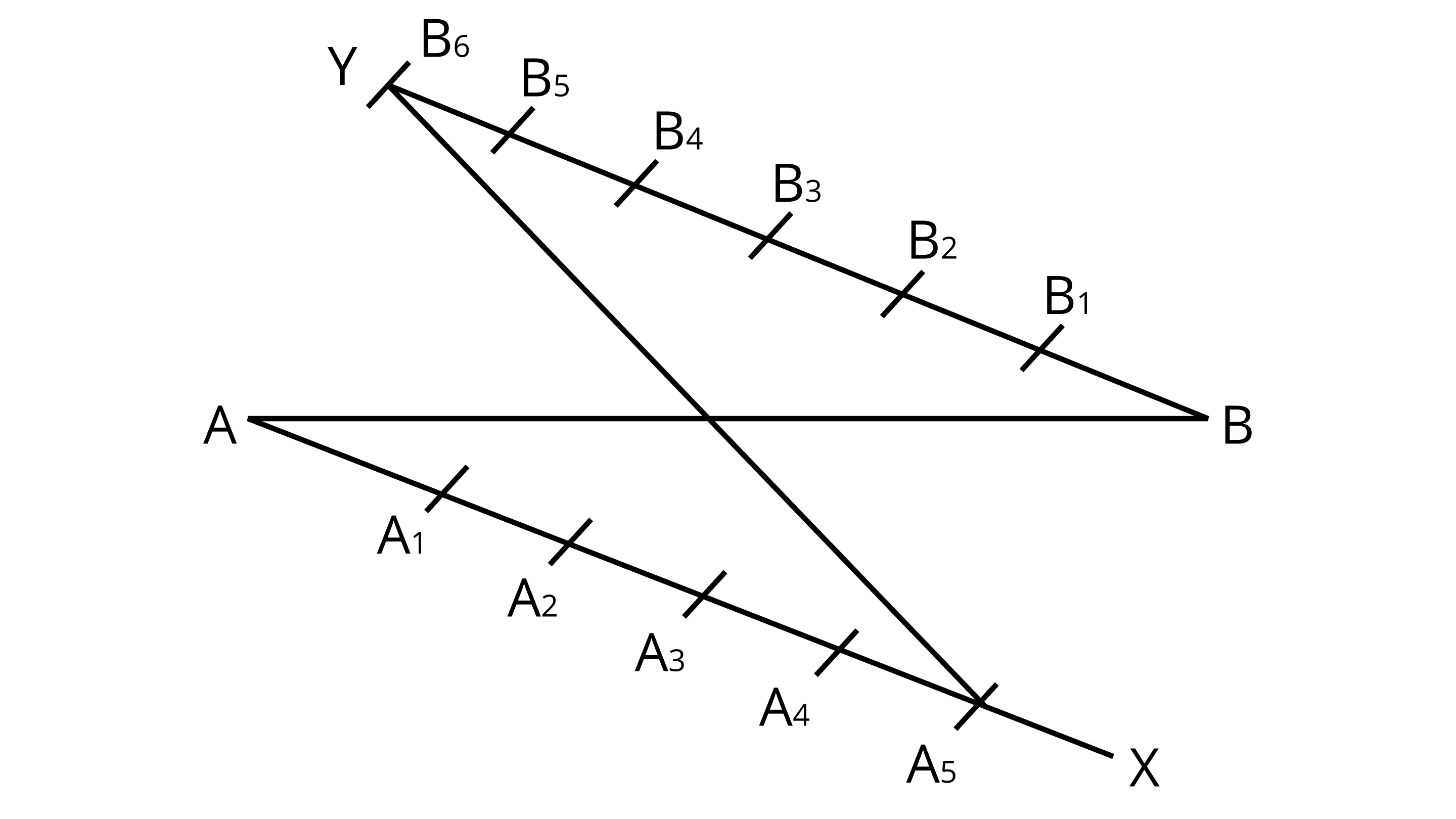
Since, the points  ${A_1},{A_2},{A_3},{A_4}$  and  ${A_5}(m = 5) $  on  $AX$  and  ${B_1},{B_2},{B_3},{B_4},{B_5}$  and  ${B_6}(n = 6) $  such that all the points are at equal distance from each other.

Therefore, join  ${B_6} and {A_5}$ .

4. To construct a triangle similar to a given  $\vartriangle ABC $  with its sides  $\dfrac{3}{7}$  of the corresponding sides of  $\vartriangle ABC $ , first draw a ray  $X$  such that  $\angle CBX$  is an acute angle and  $ X$  lies on the opposite side of  $ A $  with respect to  $C$ . Then locate points  ${B_1},{B_2},{B_3}, \ldots  $  on  $X$ at equal distances and next step is to join

(A)  ${B_{10}}$  to  $ C $ 

(B)  ${B_3}$  to  $ C $ 

(C)  ${B_7}$  to  $ C $  

(D)  ${B_4}$  to  $ C $  

Correct Answer: C

Ans: The ratio of  $3:7$ is given for a line segment $AB$. Also, it is given that a ray  $X$  is drawn so that  $\angle CBX$  is an acute angle and then at equal distances points are marked on the raY$X$.

Here, points  ${B_1},{B_2},{B_3},{B_4},{B_5},{B_6}$  and  ${B_7}$  on  ${B_x}$  at equal distance and in next step join the last point  ${B_7}$  to  $ C $ .

5. To construct a triangle similar to a given  $\vartriangle ABC $  with its sides  $\dfrac{8}{5}$  of the corresponding sides  $5$  of  $\delta ABC $  draw a ray  $X$  such that  $\angle CBX$  is an acute angle and  $ X$  is on the opposite side of  $ A $  with respect to  $C$. The minimum number of points to be located at equal distances on ray  $X$  is

(A)  $5$ 

(B)  $8$ 

(C)  $43$ 

(D)  $3$  

Correct Answer: B

Ans: To construct a triangle similar to a given triangle, with its sides  $\dfrac{m}{n}$  of the  ${\text{n}}$  corresponding sides of the given triangle the minimum number of points to be located at an equal distance is equal to the greater of  $ m $  and  ${\text{n}}$  in  $\dfrac{m}{n}$.

Here,  $\dfrac{m}{n}  =  \dfrac{8}{5}$ 

So, the minimum number of points to be located at equal distance on ray  $X$  is $8$.

6. To draw a pair of tangents to a circle that are inclined to each other at an angle of  $6{0^\circ }$, it is required to draw tangents at endpoints of those two radii of the circle, the angle between them should be

(A)  $43{5^\circ }$ 

(B)  $9{0^\circ }$ 

(C)  $6{0^\circ }$ 

(D)  $42{0^\circ}$ 

Correct Answer: D

Ans: The angle between them should be  $42{0^\circ }$  because in that case the figure is formed by the intersection point of pair of tangents, the two endpoints of those two radii (at which tangents are drawn), and the center of the circle is a quadrilateral.

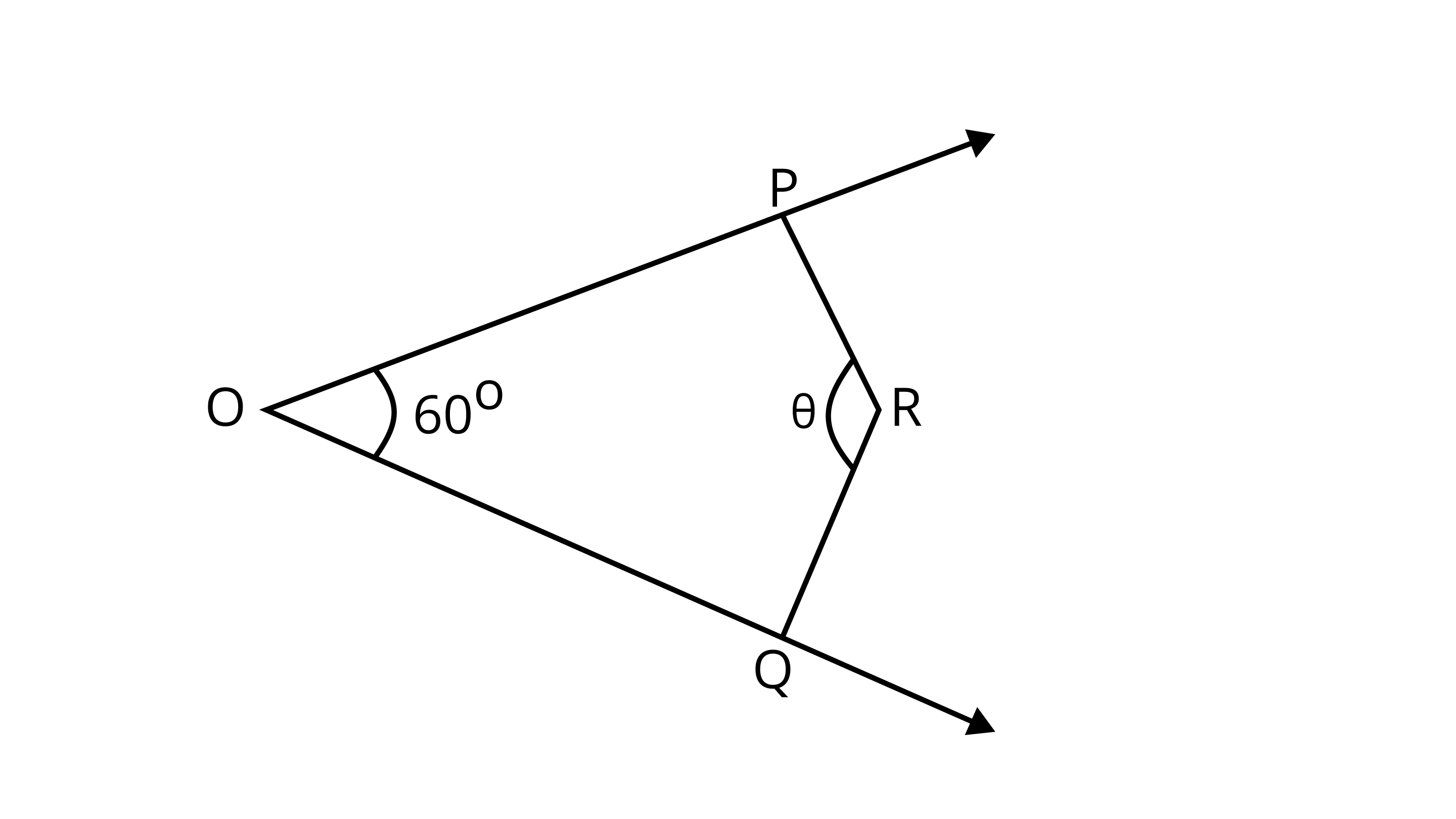
From figure it is quadrilateral, 

 $\angle {\text{POQ}} + \angle {\text{PRQ}} = {180^\circ }$ 

 $\because  $ Sum of opposite angles are  $48{0^\circ }$ 

 $\therefore {60^\circ } + {\text{}\theta{ }} = {180^\circ }$ 

 ${\text{}\theta{ }} = {120^\circ }$ 

Hence, the required angle between them is $420^\circ$.

Exercise 10.2

Write True or False and give reasons for your answer in each of the following:

1. By geometrical construction, it is possible to divide a line segment in the ratio $ \sqrt 3 :\dfrac{1}{{\sqrt 3 }}$ . 

Correct answer: This statement is True

Ans: Multiply  $ \sqrt 3  $  in each term of the given ratio.

So,  $ \sqrt 3 :\dfrac{1}{{\sqrt 3 }}$  can be simplified as  $3:1$   and  $3$  as well as  $4$  both are positive integer. 

Hence, the geometrical construction is possible to divide a line segment in the ratio $3:1$ .

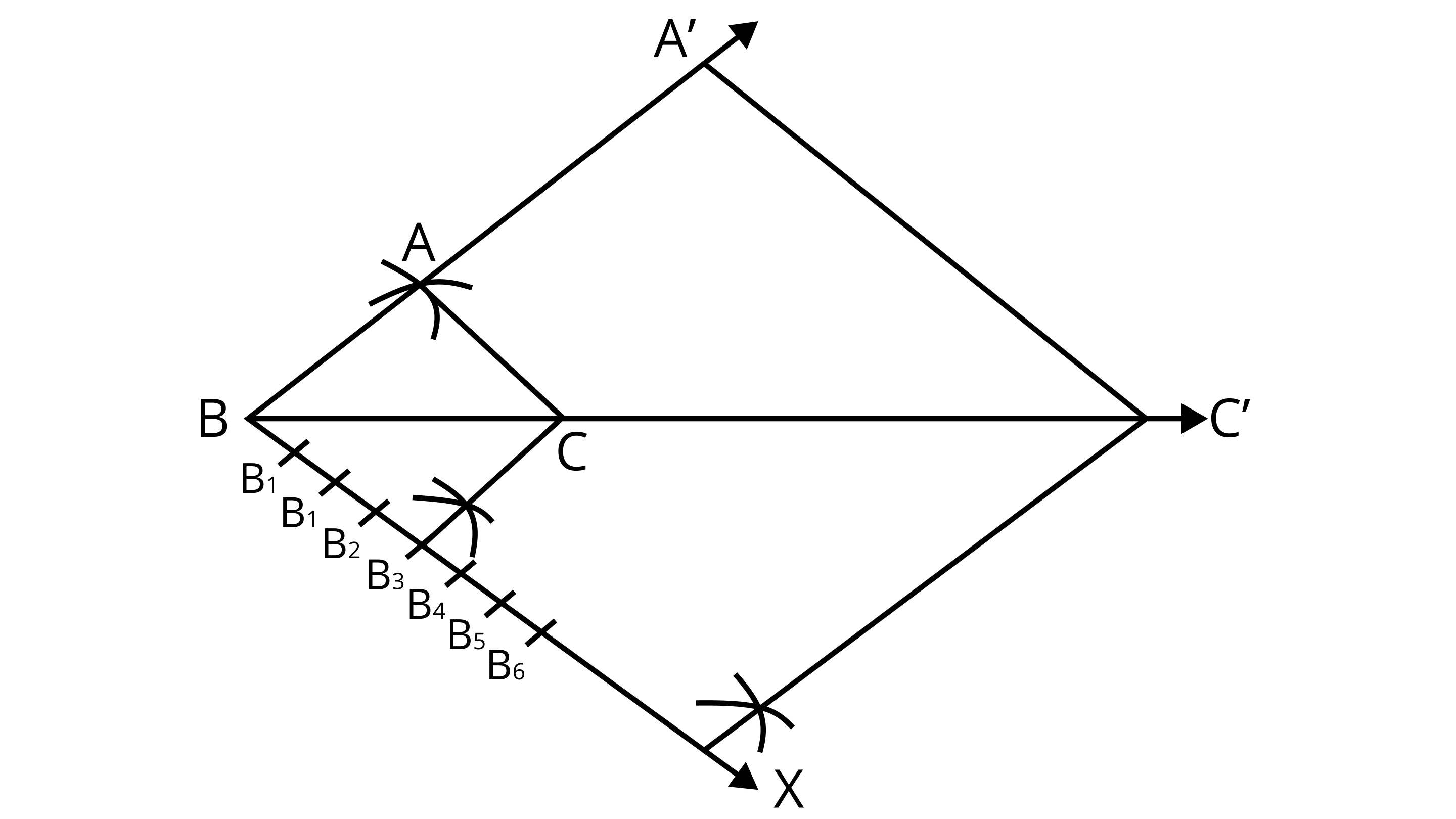
2. To construct a triangle similar to a given  $\delta ABC $  with its sides  $\dfrac{7}{3}$  of the corresponding sides of  $\vartriangle ABC$ , draw a ray BX making acute angle with  $C$  and  $ X$  lies on the opposite side of  $A$  with respect to  $C$ . The points ${B_1}$ .  ${B_2}, \ldots  \ldots ,{B_7}$  are located at equal distances on  $ BX,{B_3}$  is joined to  $ C $  and then a line segment  ${B_6}{C^\prime }$  ' is drawn parallel to  ${B_3}C $  where  ${C^\prime }$  lies on  $C$  produced. Finally, line segment  ${A^\prime }{C^\prime }$  is drawn parallel to $AC $ . 

Correct answer: The statement is False

Ans: Since,  $\delta {{\text{A}}^\prime }{\text{B}}{{\text{C}}^\prime }$  is the required triangle whose sides are  $\dfrac{7}{3}$  of the corresponding sides of $\delta {\text{ABC}}$ . Given that, segment  ${{\text{B}}_6}{{\text{C}}^\prime }$  is drawn parallel to  ${{\text{B}}_3}{\text{C}}. $  

But from our construction is never possible that segment  ${{\text{B}}_6}{{\text{C}}^\prime }$  is parallel to  ${{\text{B}}_3}{\text{C}}$  because the similar triangle  ${{\text{A}}^\prime }{\text{B}}{{\text{C}}^\prime }$  has its sides  $\dfrac{7}{3}$  of the corresponding sides of triangle ${\text{ABC}}$ .

So,  ${{\text{B}}_7}{{\text{C}}^\prime }$  is parallel to ${{\text{B}}_3}{\text{C}}$

3. A pair of tangents can be constructed from a point  $ P $  to a circle of radius  $3.5 cm$  situated at a distance of 3  $ cm$  from the center. 

Correct answer: The statement is False.

Ans: Since, the radius of the circle is  $3.5{\text{ cm}}$ 

i.e.,  $ r = 3.5{\text{ cm}}$  and a point  ${\text{P}}$  situated at a distance of  $3{\text{ cm}}$  from the centre

i.e.,  $ d = 3{\text{ cm}}$ .

We see that  $ r > d $ 

i.e., a point  ${\text{P}}$  lies inside the circle. 

So, no tangent can be drawn to a circle from a point lying inside it.

4. A pair of tangents can be constructed to a circle inclined at an angle of  $47{0^\circ }$. 

Correct answer: The statement is True.

Ans: The angle between the pair of tangents is always greater than 0 but less than  ${180^\circ }. $ 

Since the angle between the pair of tangents is always greater than 0 but less than  ${180^\circ }. $  

Hence, one can draw a pair of tangents to a circle inclined at an angle at ${170^\circ }$.

Exercise 10.3

1. Draw a line segment of length $7 cm$. Find a point  $P$  on it which divides it in the ratio $3:5$.

Ans:

Steps of construction:

1. Draw a line segment ${\text{AB}} = 7{\text{ cm}}$ .

2. Draw a raY${\text{AX}}$ , making an acute $\angle {\text{BAX}}$ .

3. Along ${\text{AX}}$ , mark  $3 + 5 = 8$  points  ${{\text{A}}_1},{{\text{A}}_2},{{\text{A}}_3},{{\text{A}}_4},{{\text{A}}_5},{{\text{A}}_6},{{\text{A}}_7},{{\text{A}}_8}$  such that  ${\text{A}}{{\text{A}}_{\text{1}}}{\text{  =  }}{{\text{A}}_{\text{1}}}{{\text{A}}_{\text{2}}}{\text{ =  }}{{\text{A}}_{\text{2}}}{{\text{A}}_{\text{3}}}{\text{  =  }}{{\text{A}}_{\text{3}}}{{\text{A}}_{\text{4}}}{\text{  =  }}{{\text{A}}_{\text{4}}}{{\text{A}}_{\text{5}}}{\text{  =  }}{{\text{A}}_{\text{6}}}{{\text{A}}_{\text{7}}}{\text{  =  }}{{\text{A}}_{\text{7}}}{{\text{A}}_{\text{8}}}$ 

4. Join ${{\text{A}}_8}{\text{B}}$ .

5. From ${{\text{A}}_{\text{3}}}$ ,  $\operatorname{draw} {{\text{A}}_{\text{3}}}{\text{P}}\parallel {{\text{A}}_{\text{8}}}{\text{B}}$  meeting  ${\text{AB}}$  at ${\text{P}}$ .

By making an angle equal to  $\angle {\text{B}}{{\text{A}}_8}{\text{A}}$  at  $ \left. {{{\text{A}}_3}} \right]$  Then,  ${\text{P}}$  is the point on  ${\text{AB}}$  which divides it in the ratio $3:5$ .

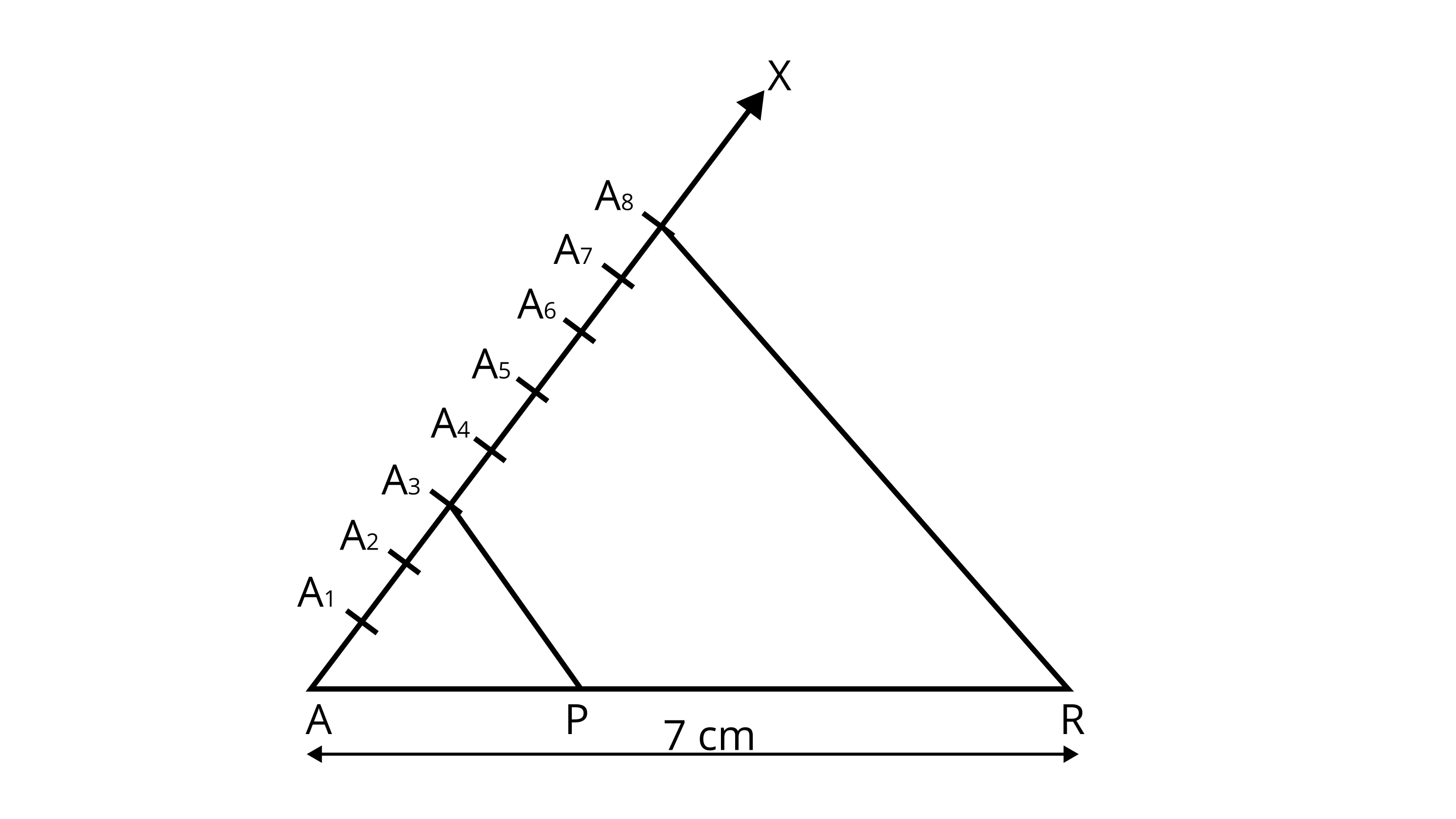
Justification:

Let  ${\text{A}}{{\text{A}}_1} = {{\text{A}}_1}{{\text{A}}_2} = {{\text{A}}_2}{{\text{A}}_3} = {{\text{A}}_3}{{\text{A}}_4} =  \ldots  \ldots  \ldots  = {{\text{A}}_7}{{\text{A}}_8} = {\text{X}}$ 

In $\delta {\text{AB}}{{\text{A}}_8}$ , we have

 ${{\text{A}}_3}{\text{P}}\parallel {{\text{A}}_8}{\text{B}}$ 

Hence,  ${\text{AP}}:{\text{PB}} = 3:5$ .

2. Draw a right triangle  $ABC $  in which  $C = 12 cm,AB = 5 cm$  and  $\angle B = 9{0^\circ }.$  Construct a triangle similar to it and of scale factor $\dfrac{2}{3}$ . Is the new triangle also a right triangle? 

Ans:

Steps of construction:

1. Draw a line segment ${\text{BC}} = 12{\text{ cm}}$ .

2. From B draw a line  ${\text{AB}} = 5{\text{ cm}}$  which makes right angle at  ${\text{B}}$ 

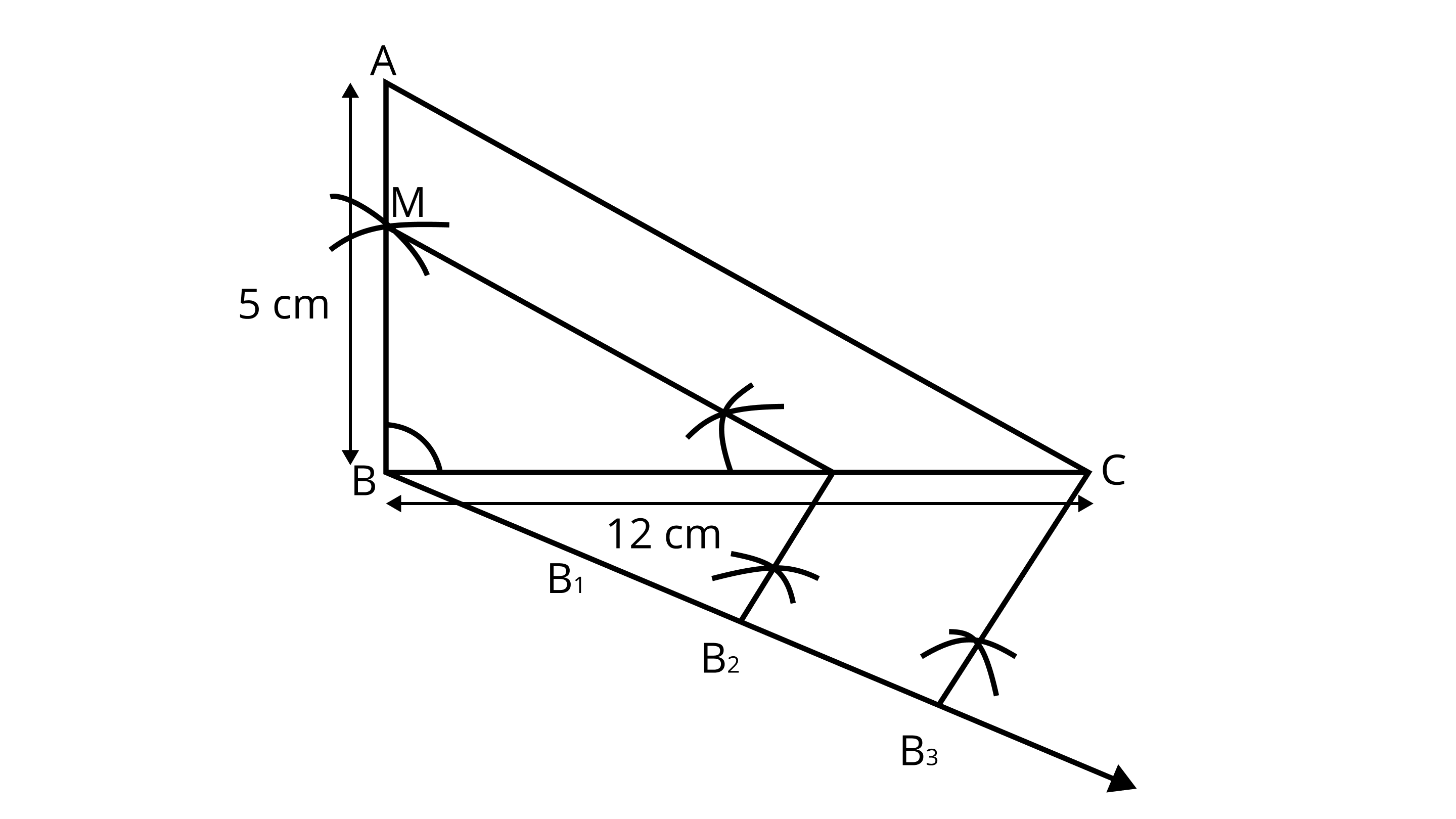
3. Join  ${\text{AC}},\Delta {\text{ABC}}$  is the given right triangle.

4. From B draw an acute  $\angle {\text{CBY}}$  downwards.

5. On ray BY, mark three points  ${{\text{B}}_1},{{\text{B}}_2}$  and ${{\text{B}}_3}$ , such that  ${\text{B}}{{\text{B}}_1} = {{\text{B}}_1}{{\text{B}}_2} = {{\text{B}}_2}{{\text{B}}_3}$ . 

6. Join ${{\text{B}}_3}{\text{C}}$ .

7. From point  ${{\text{B}}_2}$  draw  ${{\text{B}}_{\text{2}}}{\text{N}}\parallel {{\text{B}}_{\text{3}}}{\text{C}}$  intersect  ${\text{BC}}$  at ${\text{N}}$ .

8. From point  ${\text{N}}$  draw  ${\text{NM}}\parallel {\text{CA}}$ intersect  ${\text{BA}}$  at ${\text{M}}$ .  $\delta {\text{MBN}}$  is the required triangle.  $\delta {\text{MBN}}$  is also a right angled triangle at  ${\text{B}}$ .

3. Draw a triangle  $ABC$  in which  $C = 6cm,CA = 5cm$  and  $AB = 4cm$ . Construct a triangle similar to it and of scale factor  $\dfrac{5}{3}$ 

Ans:

Steps of construction:

1. Draw a line segment ${\text{BC}} = 6{\text{ cm}}$ .

2. Taking  ${\text{B}}$  and  ${\text{C}}$  as centres, draw two arcs of radii  $4{\text{ cm}}$  and  $5{\text{ cm}}$  intersecting each other at A.

3. Join  ${\text{BA}}$  and  ${\text{CA}}.\Delta {\text{ABC}}$  is the required triangle

4. From ${\text{B}}$ , draw any ray  $ B X$  downwards making at acute angle  $\angle {\text{CBX}}$ 

5. Mark five points  ${{\text{B}}_1},{{\text{B}}_2},{{\text{B}}_3},{{\text{B}}_4}$  and  ${{\text{B}}_5}$  on ${\text{BX}}$ , such that ${\text{B}}{{\text{B}}_1} = {{\text{B}}_1}{{\text{B}}_2} = {{\text{B}}_2}{{\text{B}}_3} = {{\text{B}}_3}{{\text{B}}_4} = {{\text{B}}_4}{{\text{B}}_5}$ .

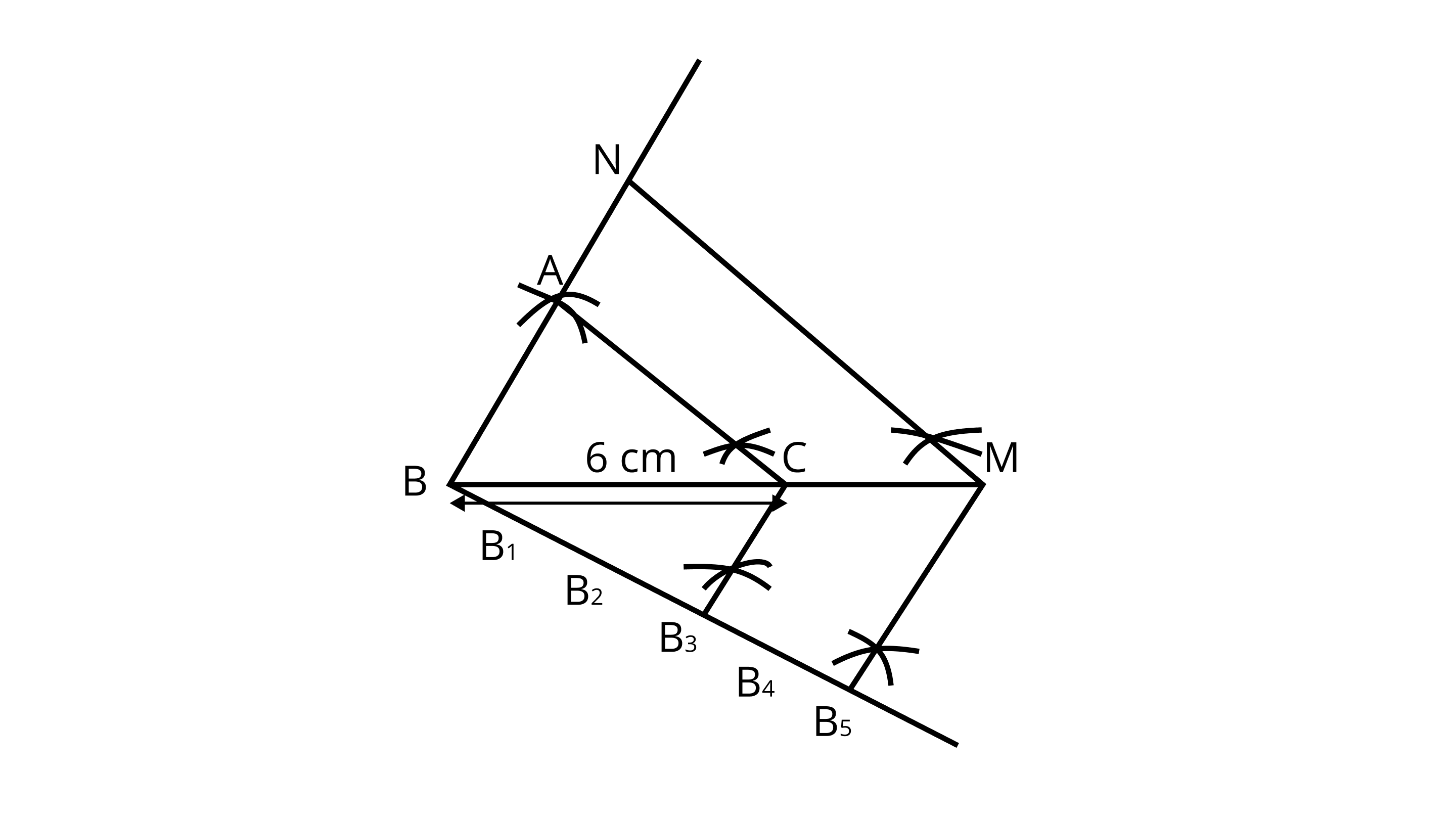
6. Join  ${{\text{B}}_{\text{3}}}{\text{C}}$  and from  ${{\text{B}}_{\text{5}}}$  draw  ${{\text{B}}_{\text{5}}}{\text{M}}\parallel {{\text{B}}_{\text{3}}}{\text{C}}$  intersecting the extended line segment  ${\text{BC}}$  at ${\text{M}}$ .

7. From point  ${\text{M}}$  draw  ${\text{MN}}\parallel {\text{CA}}$  intersecting the extended line segment  ${\text{BA}}$  at ${\text{N}}$ .

Then,  $\delta {\text{NBM}}$  is the required triangle whose sides is equal to  $\dfrac{5}{3}$  of the corresponding sides of the $\vartriangle {\text{ABC}}$ .

Hence,  $\delta {\text{NBM}}$  is the required triangle.

4. Construct a tangent to a circle of radius  $4 cm$  from a point which is at a distance of  $6 cm$  from its centre.

Ans:

Steps of construction:

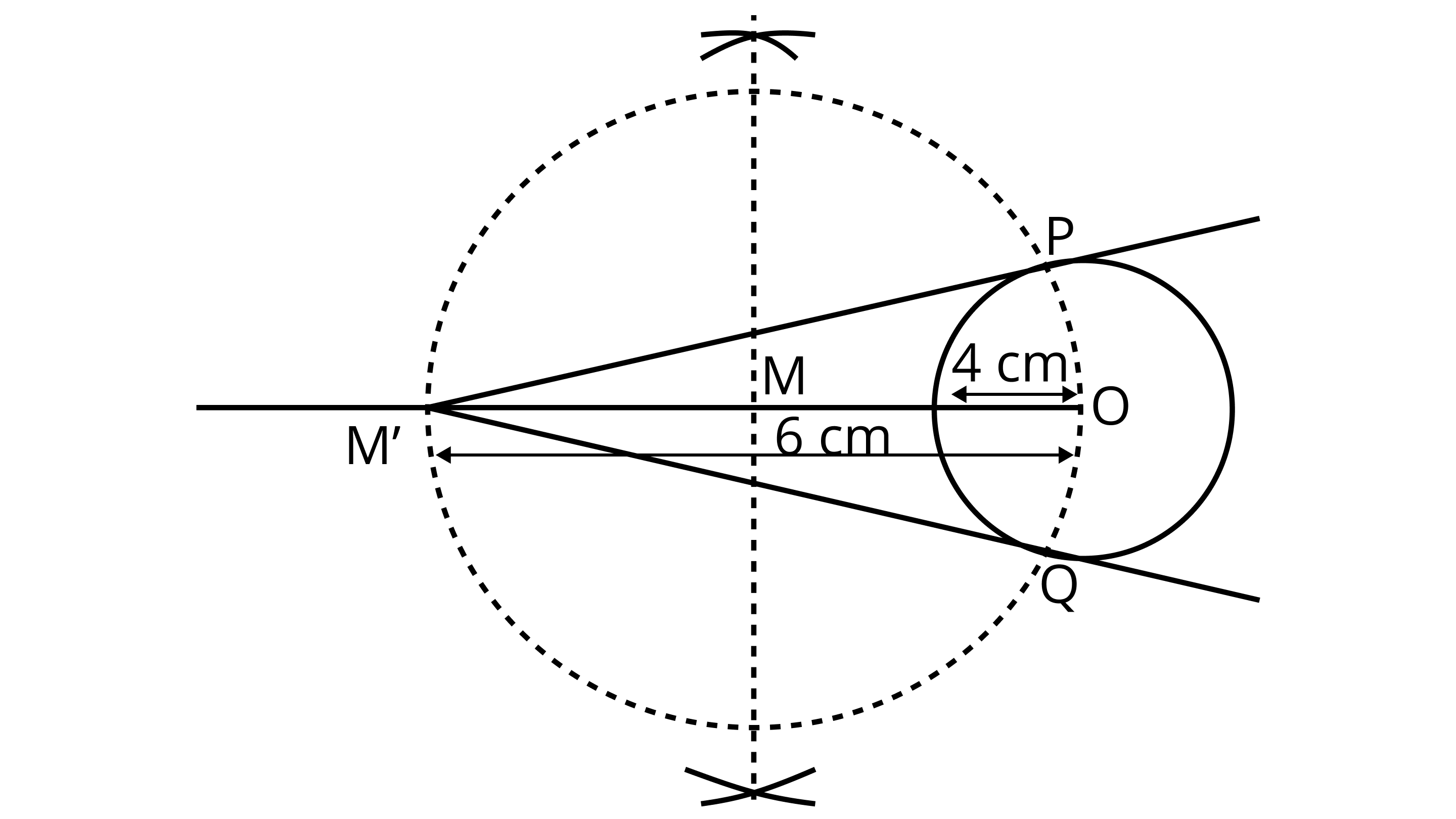
1. Draw a circle of radius $4{\text{ cm}}$ . Let centre of this circle is ${\text{O}}$ .

2. Join \[{\text{OM}}'\] and bisect it. Let  ${\text{M}}$  be mid-point of\[{\text{OM}}'\].

3. Taking  ${\text{M}}$  as centre and  ${\text{MO}}$  as radius draw a circle to intersect circle  $(0,4)$  at two points,  ${\text{P}}$  and ${\text{Q}}$ .

4. Join  PM'  and  QM' . PM' and QM'  are the required tangents from M' to circle  ${\text{C}}(0,4)$.

Exercise 10.4

1. Two line segments  $AB$  and  $AC$  include an angle of  $60^\circ$  where \[AB = 5 cm\] and $AC = 7 cm$ . Locate points  $P$  and  $Q$  on  $AB$  and $AC$ , respectively such that  $AP = \dfrac{3}{4}AB$  and $AQ = \dfrac{1}{4}AC$ . Join  $P$  and  $Q$ and measure the length  $PQ$ .

Ans:

From equation (i) 

${\text{AP}} = \dfrac{3}{4} \cdot {\text{AB}}$  

$= \dfrac{3}{4} \times 5$  

$= \dfrac{{15}}{4}{\text{ cm}}$  

Then, 

${\text{PB}} = {\text{AB}} - {\text{AP}}$  

$= 5 - \dfrac{{15}}{4}$  

$= \dfrac{{20 - 15}}{4}$  

$= \dfrac{5}{4}{\text{ cm}}$  

$\because {\text{P}}$  is any point on the ${\text{AB}}$  

$\therefore {\text{AP}}:{\text{PB}} = \dfrac{{15}}{4}:\dfrac{5}{4} = {\text{AP}}:{\text{PB}} = 3:1$ 

i.e., scale factor of line segment  ${\text{AB}}$  is  $\dfrac{3}{1}$  

Again from equation (i),

${\text{AQ}} = \dfrac{1}{4}{\text{AC}}$  

$= \dfrac{1}{4} \times 7$  

$= \dfrac{7}{4}{\text{ cm }}$  

Then,

${\text{QC}} = {\text{AC  -  AQ}}$  

$= 7 - \dfrac{7}{4}$  

$= \dfrac{{28 - 7}}{4}$  

$= \dfrac{{21}}{4}{\text{ cm}}$

${\text{Q}}$  is any point on the AC

$\therefore {\text{AQ}}:{\text{QC}} = \dfrac{7}{4}:\dfrac{{21}}{4}$ 

${\text{                }} = 1:3$   

${ \Rightarrow AQ:QC = 1:3}$ 

i.e., scale factor of line segment  ${\text{AC}}$  is  $\dfrac{1}{3}$ .

Steps of construction:

1. Draw a line segment ${\text{AB}} = 5{\text{ cm}}$

2. Now draw a ray  ${\text{AZ}}$  making an acute $\angle {\text{BAZ}} = {60^\circ }$ .

3. With  ${\text{A}}$  as centre and radius equal to  $7{\text{ cm}}$  draw an arc cutting the line  ${\text{AZ}}$  at ${\text{C}}$ .

4. Draw a raY${\text{AX}}$ , making an acute $\angle {\text{BAX}}$ .

5. Along ${\text{AX}}$ , mark  $4 + 3 = 4$  points ${{\text{A}}_1},{{\text{A}}_2},{{\text{A}}_3}$  and ${{\text{A}}_4}$  such that ${\text{A}}{{\text{A}}_{\text{1}}}{\text{ =  }}{{\text{A}}_{\text{1}}}{{\text{A}}_{\text{2}}}{\text{ =  }}{{\text{A}}_{\text{2}}}{{\text{A}}_{\text{3}}}{\text{ =  }}{{\text{A}}_{\text{3}}}{{\text{A}}_{\text{4}}}$ .

6. Join ${{\text{A}}_4}{\text{B}}$ .

7. From  ${{\text{A}}_{\text{3}}}$  draw ${{\text{A}}_{\text{3}}}{\text{P}}\parallel {{\text{A}}_{\text{4}}}{\text{B}}$  meeting ${\text{AB}}$  at  ${\text{P}}$ 

By making an angle equal to  $\angle {\text{A}}{{\text{A}}_4}{\text{B}}$.

Then,  ${\text{P}}$  is the point on ${\text{AB}}$ which divides it in the ratio $3:1$ .

So,  ${\text{AP : PB  =  3 : 1}}$ .

8. Draw a raY ${\text{AY}}$ , making an acute $\angle {\text{CAY}}$ .

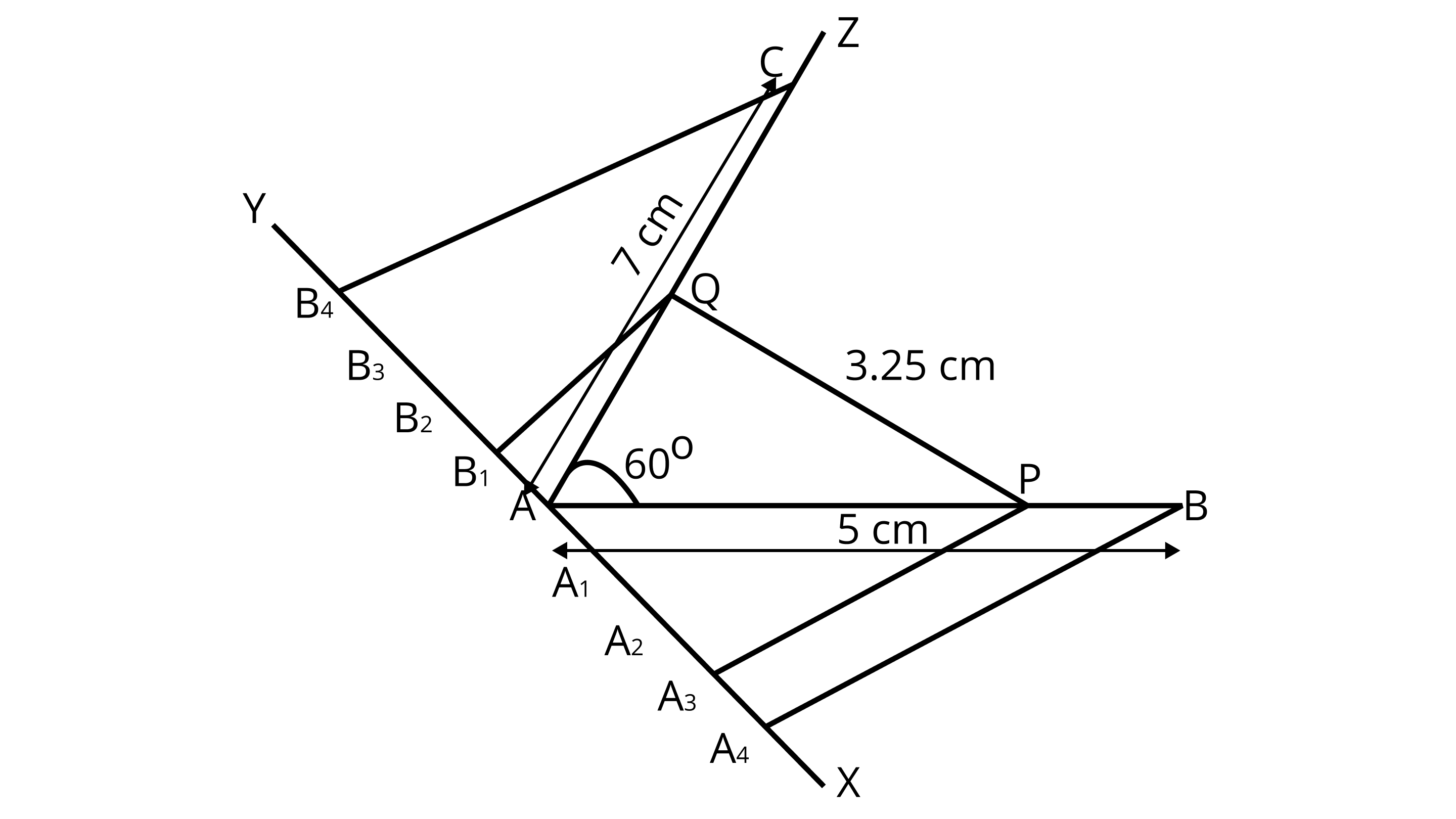
9. Along AY, mark $3+1=4$ points $\mathrm{B}_{1}, \mathrm{~B}_{2}, \mathrm{~B}_{3}$ and $\mathrm{B}_{4}$.

Such that $\mathrm{AB}_{1}=\mathrm{B}_{1} \mathrm{~B}_{2}=\mathrm{B}_{2} \mathrm{~B}_{3}=\mathrm{B}_{3} \mathrm{~B}_{4}$.

10. Join $\mathrm{B}_{4} \mathrm{C}$.

11. From $\mathrm{B}_{1}$ draw $\mathrm{B}_{1} \mathrm{Q} \| \mathrm{B}_{4} \mathrm{C}$ meeting $\mathrm{AC}$ at $\mathrm{Q}$ 

i.e. by making an angle equal to $\angle \mathrm{AB}_{4} \mathrm{C}$.

Then, $\mathrm{Q}$ is the point on $\mathrm{AC}$ which divides it in the ratio $4: 3$.

So, $\mathrm{AQ}: \mathrm{QC}=1: 3$

12. Finally, join $\mathrm{PQ}$ and its measurement is $3.25 \mathrm{~cm}$.

2. Draw a parallelogram  $ABCD$  in which  $C  =  5cm, AB  = 3cm$  and $\angle ABC = 6{0^\circ }$ , divide it into triangles BCD and  $ABD$  by the diagonal  $D$ . Construct the triangle BD'C' similar to  $\vartriangle BDC$  with scale factor $\dfrac{4}{3}$ . Draw the line segment  D'A'  parallel to  $DA$  where A' lies on extended side $A$ . Is A'BC'D' parallelogram? 

Ans:

Steps of construction:

1. Draw a line segment  ${\text{AB  = 3cm}}$ .

2. Now, draw a ray by making an acute $\angle {\text{ABY}} = {60^\circ }$ .

3. With  ${\text{B}}$  as centre and radius equal to  $5{\text{ cm}}$  draw an arc cut the point Con  ${\text{BY}}$ .

4. Again draw a ray  ${\text{AZ}}$  making an acute $\angle {\text{ZA}}{{\text{X}}^\prime } = {60^\circ }$ .

 $\left[ {\because {\text{BY}}\parallel {\text{AZ}},{\text{ }}\therefore {\text{YB}}{{\text{X}}^\prime } = {\text{ZA}}{{\text{X}}^\prime } = {{60}^\circ }} \right]$ 

5. With  ${\text{A}}$  as centre and radius equal to  $5{\text{ cm}}$  draw an arc cut the point  ${\text{D}}$  on  ${\text{AZ}}$ .

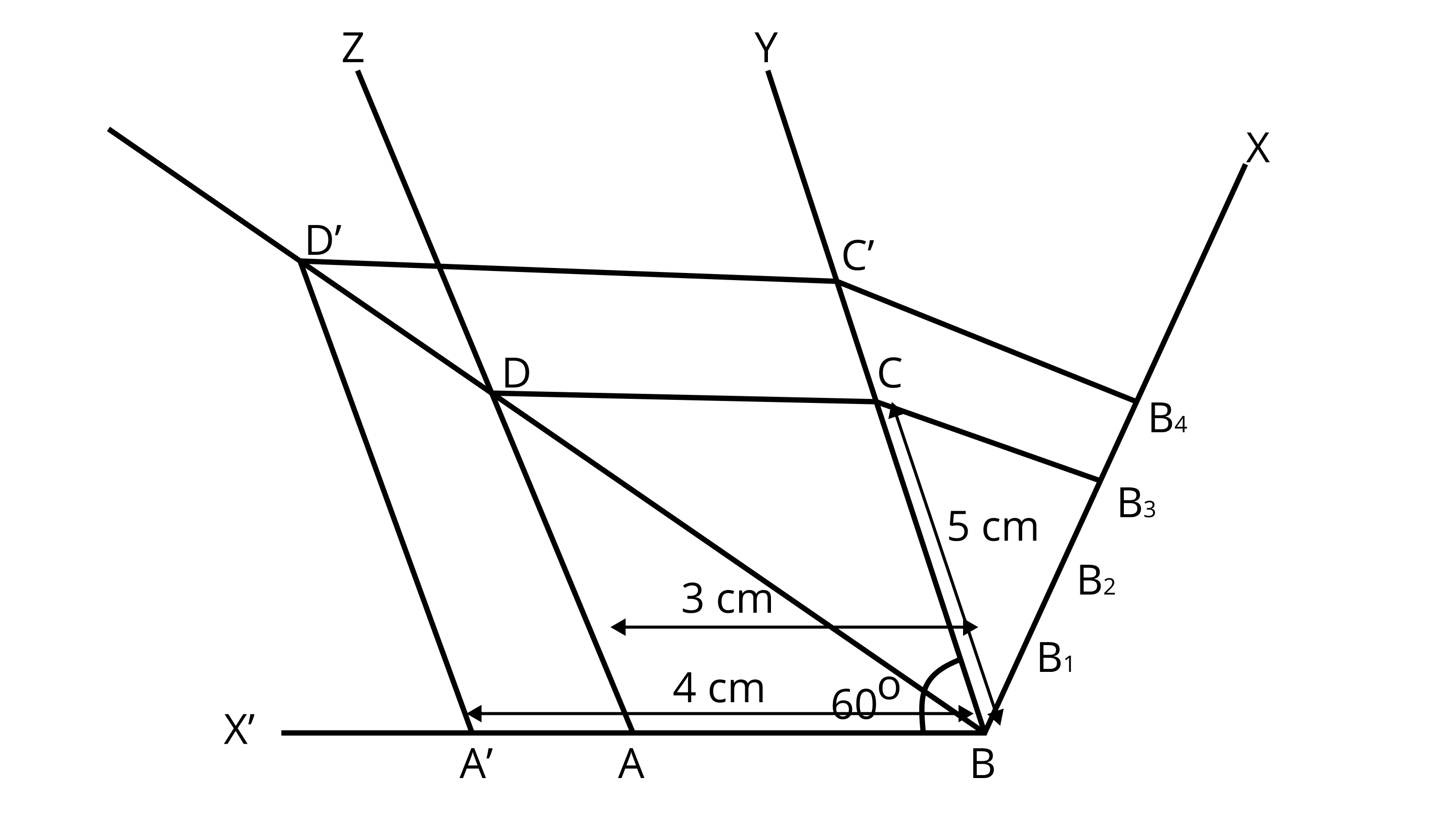
6. Now, join  ${\text{CD}}$  and finally make a parallelogram ${\text{ABCD}}$ .

7. Join  ${\text{BD}}$ , which is a diagonal of parallelogram  ${\text{ABCD}}$ .

8. From  ${\text{B}}$  draw any ray  ${\text{BX}}$  downwards making an acute  $\angle {\text{CBX}}$ .

9. Locate 4 points ${{\text{B}}_{\text{1}}}{\text{,}}{{\text{B}}_{\text{2}}}{\text{,}}{{\text{B}}_{\text{3}}}{\text{,}}{{\text{B}}_{\text{4}}}$ , on  $ B X$ , such that  $ B{B_1} = {B_1}{B_2} = {B_2}{B_3} = {B_3}{B_4}$ .

10. Join  ${{\text{B}}_3}{\text{C}}$  and from  ${{\text{B}}_4}$  draw a line  ${{\text{B}}_{\text{4}}}{{\text{C}}^{\text{'}}}\parallel {{\text{B}}_{\text{3}}}{\text{C}}$  intersecting the extended line segment  ${\text{BC}}$  at ${\text{C}}$ .

11. From point $\mathrm{C}$ draw C'D' || C D intersecting the extended line segment $\mathrm{BD}$ at $\mathrm{D}^{\prime}$. Then, $\triangle \mathrm{D}^{\prime} \mathrm{BC}$ ' is the required triangle whose sides are $\frac{4}{3}$ of the corresponding sides of $\triangle \mathrm{DBC}$.

12. Now draw a line segment D'A' parallel to ${\text{DA}}$ , where  ${{\text{A}}^\prime }$  lies on extended side  BA  i.e., a ray  BX' . 

13. Finally, we observe that  ${{\text{A}}^\prime }{\text{B}}{{\text{C}}^\prime }{{\text{D}}^\prime }$  ' is a parallelogram in which  ${{\text{A}}^\prime }{{\text{D}}^\prime } = 6.5{\text{cm , }}{{\text{A}}^\prime }{\text{B}} = 4{\text{cm}}$  and  $\angle {{\text{A}}^\prime }{\text{B}}{{\text{D}}^\prime } = {60^\circ }$ divide it into triangles  ${\text{B}}{{\text{C}}^\prime }{{\text{D}}^\prime }$  and  ${{\text{A}}^\prime }{\text{B}}{{\text{D}}^\prime }$  by the diagonal  ${\text{BD}}$'.

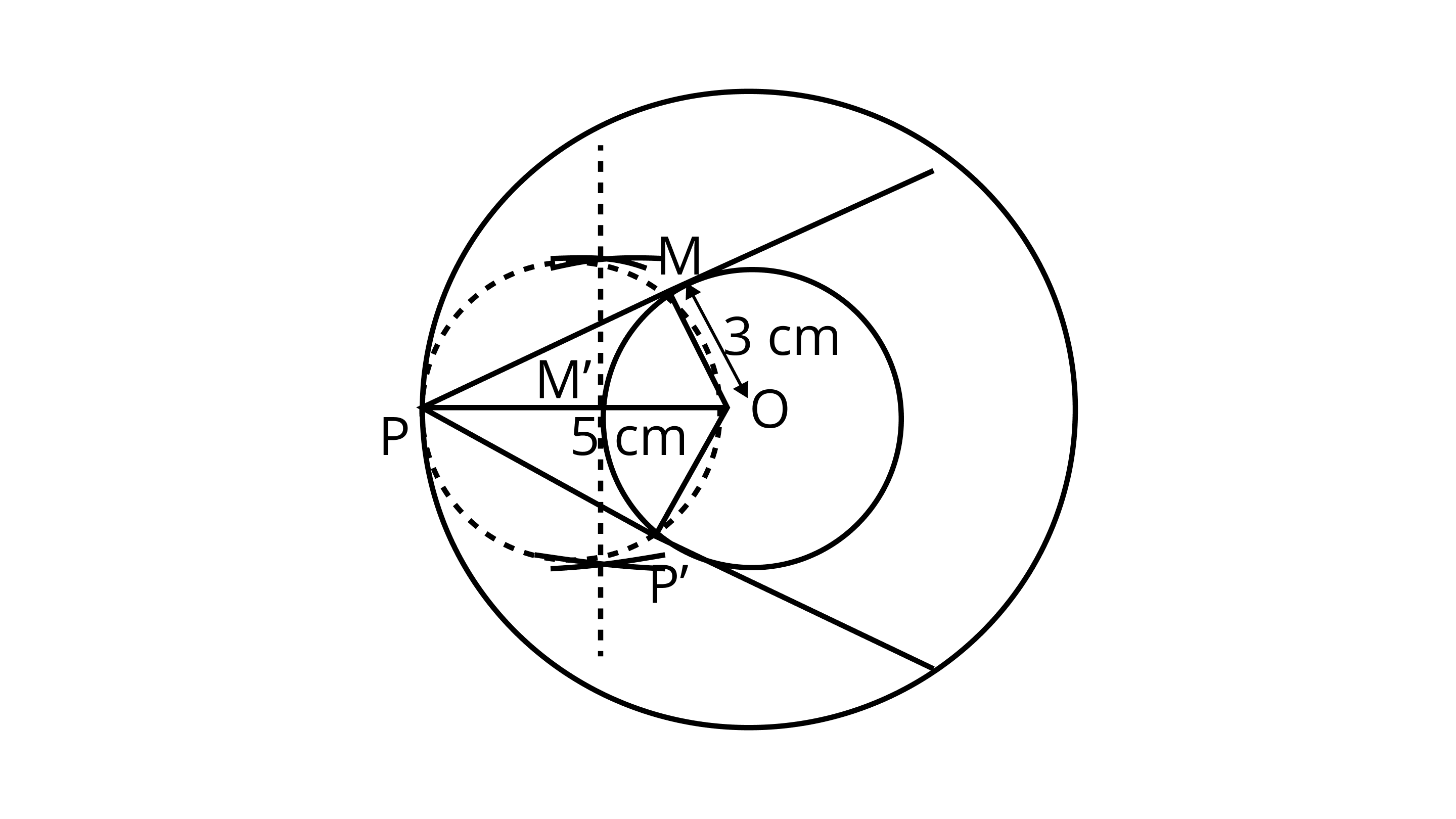
3. Draw two concentric circles of radii  $3cm$  and $5 cm$. Taking a point on the outer circle constructs the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation. 

Ans: Given, two concentric circles of radii  $3{\text{cm}}$  and  $5{\text{ cm}}$  with centre 0. We have to draw pair of tangents from point  ${\text{P}}$  on the outer circle to the other.

Steps of construction:

1. Draw two concentric circles with centre  ${\text{O}}$  and radii  $3{\text{cm}}$  and $5{\text{ cm}}$ .

2. Taking any point  ${\text{P}}$  on outer circle. Join ${\text{OP}}$ .

3. Bisect ${\text{OP}}$ , let  ${{\text{M}}^\prime }$  be the mid-point of ${\text{OP}}$ . Taking  ${{\text{M}}^\prime }$  as centre and  ${\text{O}}{{\text{M}}^\prime }$  as radius draw a circle dotted which cuts the inner circle at  ${\text{M}}$  and  ${{\text{P}}^\prime }$ .

4. Join  ${\text{PM}}$  and  ${\text{P}}{{\text{P}}^\prime }$ . Thus,  ${\text{PM}}$  and  ${\text{P}}{{\text{P}}^\prime }$  are the required tangents.

5. On measuring  ${\text{PM}}$  and  ${\text{P}}{{\text{P}}^\prime }$ , we find that  ${\text{PM}} = {\text{P}}{{\text{P}}^\prime } = 4{\text{ cm}}$ .

Actual calculation:

In right angle $\triangle \mathrm{OMP}, \angle \mathrm{PMO}=90^{\circ}$

$\mathrm{PM}^{2}=\mathrm{OP}^{2}-\mathrm{OM}^{2}$

By Pythagoras theorem i.e.

$(\text{hypotenuse})^{2}=(\text { base })^{2}+(\text { perpendicular })^{2}$

$\Rightarrow \mathrm{PM}^{2}=(5)^{2}-(3)^{2}$

$\Rightarrow 25-9=16$

$\Rightarrow \mathrm{PM}=4 \mathrm{~cm}$

Hence, the length of both tangents is $4 \mathrm{~cm}$.

4. Draw an isosceles triangle  $ABC$  in which  $AB  =  AC  =  6cm$  and  $C  =  5cm$ . Construct a triangle PBR similar to  $ABC$  in which $PB = 8 cm$ . Also justify the construction.

Ans:

Let  $\delta {\text{PQR}}$  and  $\delta {\text{ABC}}$  are similar triangles, then its scale factor between the corresponding side is  $\dfrac{{PQ}}{{AB}} = \dfrac{8}{6} =  $   $\dfrac{4}{3}$ 

Steps of construction:

1. Draw a line segment ${\text{BC  =  5cm}}$ .

2. Construct OQ the perpendicular bisector of line segment  ${\text{BC}}$  meeting  ${\text{BC}}$  at  ${{\text{P}}^\prime }$ .

3. Taking  ${\text{B}}$  and  ${\text{C}}$  as centres draw two arcs of equal radius  ${\text{6cm}}$  intersecting each other at  ${\text{A}}$ .

4. Join  ${\text{BA}}$  and  ${\text{CA}}$ . So,  $\delta {\text{ABC}}$  is the required isosceles triangle.

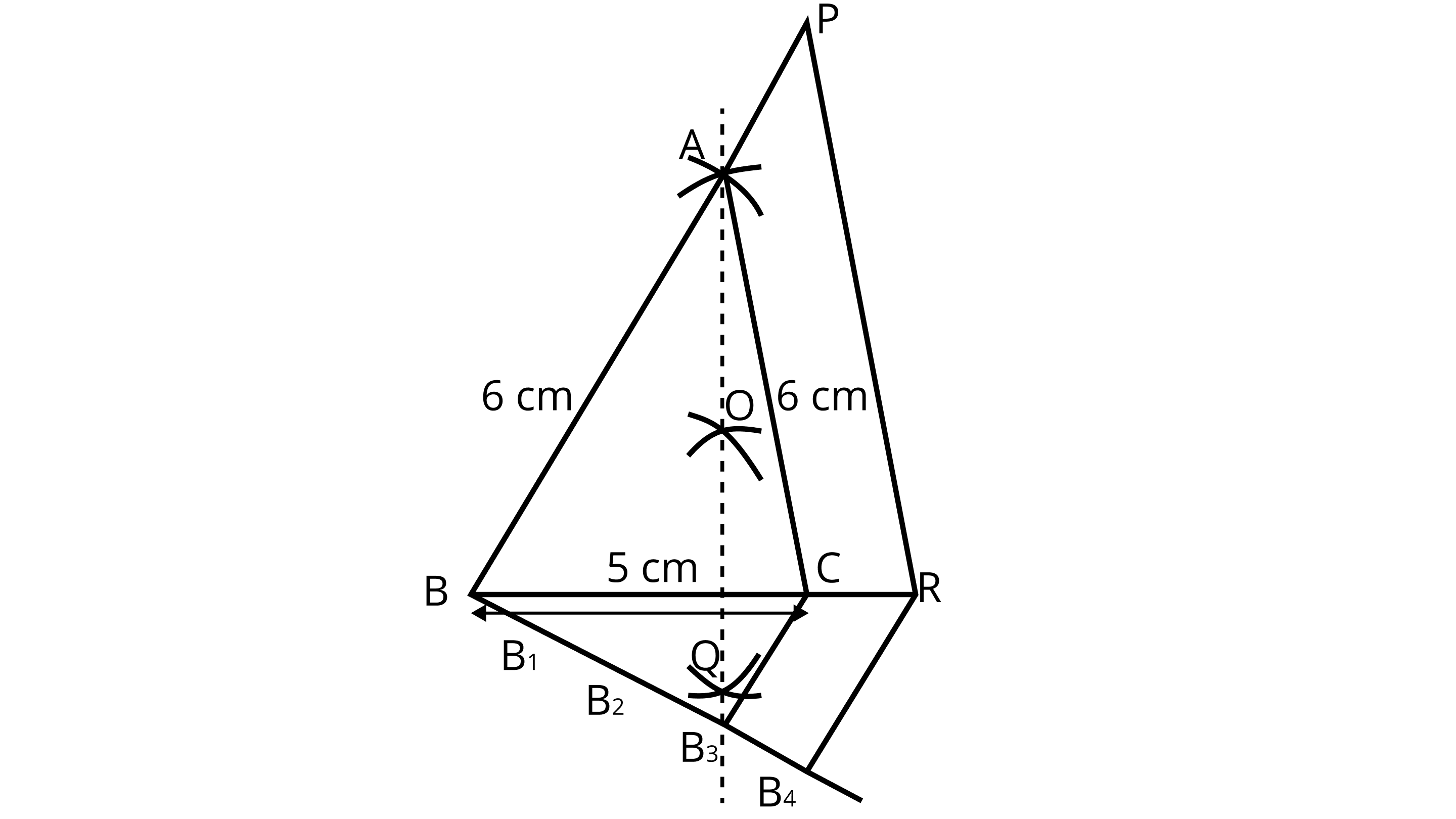
5. From  ${\text{B}}$ , draw any ray  ${\text{BX}}$  making an acute $\angle {\text{CBX}}$ .

6. Locate four points  ${{\text{B}}_{\text{1}}}{\text{,}}{{\text{B}}_{\text{2}}}{\text{,}}{{\text{B}}_{\text{3}}}$  and  ${{\text{B}}_{\text{4}}}$  on  ${\text{BX}}$  such that ${\text{B}}{{\text{B}}_{\text{1}}}{\text{ =  }}{{\text{B}}_{\text{1}}}{{\text{B}}_{\text{2}}}{\text{ =  }}{{\text{B}}_{\text{2}}}{{\text{B}}_{\text{3}}}{\text{ =  }}{{\text{B}}_{\text{3}}}{{\text{B}}_{\text{4}}}$ .

7. Join  ${{\text{B}}_3}{\text{C}}$  and from  ${{\text{B}}_4}$  draw a line  ${{\text{B}}_4}{\text{R}}\parallel {{\text{B}}_3}{\text{C}}$  intersecting the extended line segment  ${\text{BC}}$  at  ${\text{R}}$ 

8. From point  ${\text{R}}$ , draw  ${\text{RP}}\parallel {\text{CA}}$  meeting  ${\text{BA}}$  produced at  ${\text{P}}$ . Then,  $\delta {\text{PBR}}$  is the required triangle.

Justification:

$\because {{\text{B}}_4}{\text{R}}\parallel {{\text{B}}_3}{\text{C}}$  (by construction)

$\dfrac{{{\text{BC}}}}{{{\text{CR}}}}{\text{ =  }}\dfrac{{\text{3}}}{{\text{1}}} \Rightarrow \dfrac{{{\text{CR}}}}{{{\text{BC}}}}{\text{ = }}\dfrac{{\text{1}}}{{\text{3}}}$ 

Now, 

$\dfrac{{{\text{BR}}}}{{{\text{BC}}}}{\text{ = }}\dfrac{{{\text{BC + CR}}}}{{{\text{BC}}}}$  

${\text{ =  1 + }}\dfrac{{{\text{CR}}}}{{{\text{BC}}}}$  

${\text{ = 1 + }}\dfrac{{\text{1}}}{{\text{3}}}$ 

${\text{ = }}\dfrac{{\text{4}}}{{\text{3}}}$ 

Also,  ${\text{RP}}\parallel {\text{CA}}$  $\therefore \quad \vartriangle {\text{ABC}}$ proportionate to $\Delta {\text{PBR}}$ 

and  $\dfrac{{{\text{PB}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{RP}}}}{{{\text{CA}}}}{\text{ = }}\dfrac{{{\text{BR}}}}{{{\text{BC}}}}{\text{ = }}\dfrac{{\text{4}}}{{\text{3}}}$ .

5. Draw a triangle  $ABC$  in which  $AB  =  5cm,BC  =  6cm$  and  $\angle ABC = 6{0^\circ }$ . Construct a triangle similar to  $ABC $  with scale factor $\dfrac{5}{7}$ . Justify the construction. 

Ans:

Steps of construction:

1. Draw a line segment ${\text{AB  =  5cm}}$ .

2. From point ${\text{B}}$ , draw  $\angle {\text{ABY}} = {60^\circ }$  on which take ${\text{BC  =  6cm}}$ .

3. Join  ${\text{AC, \Delta ABC}}$  is the required triangle.

4. From ${\text{A}}$ , draw any ray  ${\text{AX}}$  downwards making an acute angle  $\angle {\text{BAX}}$ 

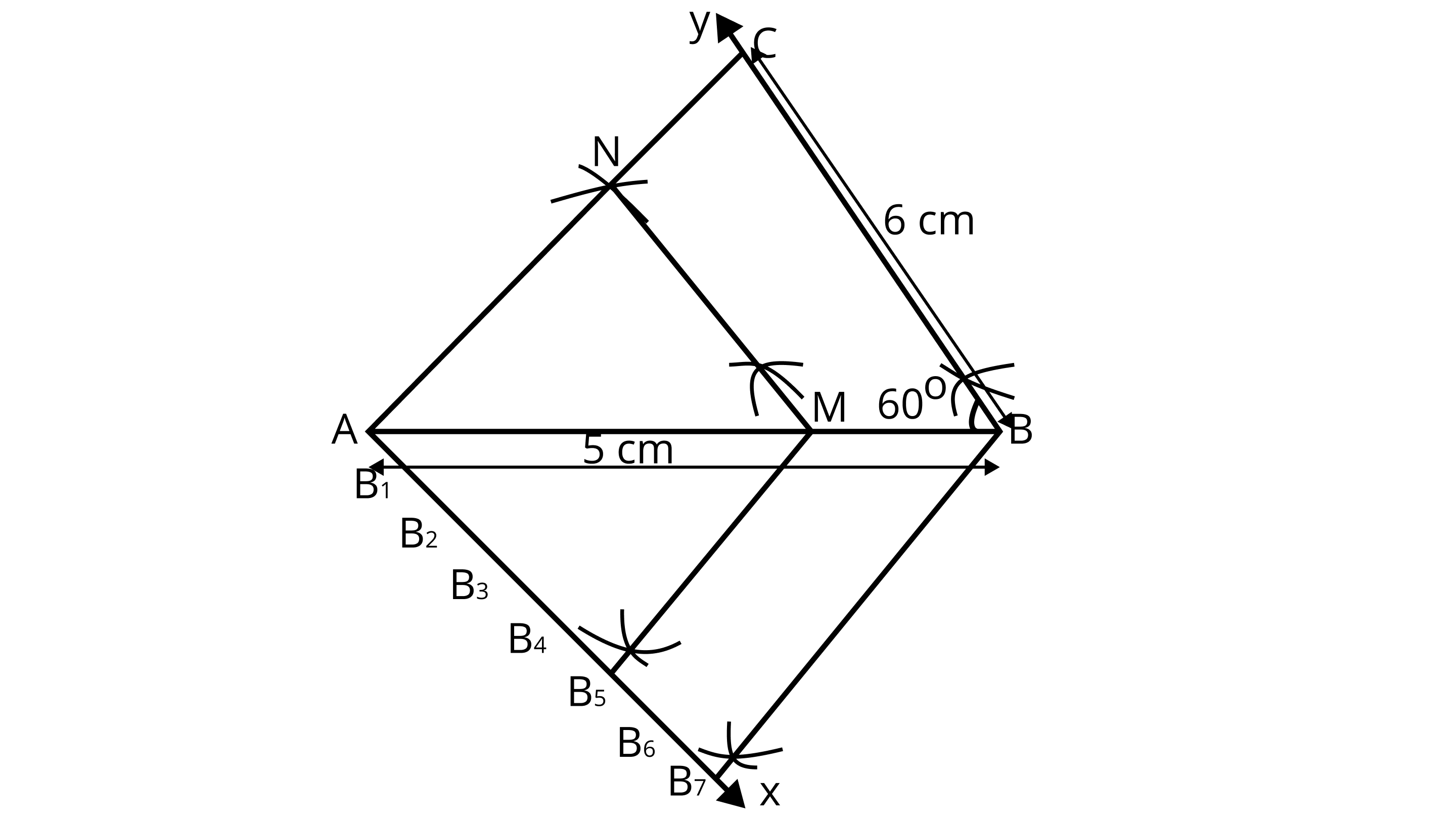
5. Mark 7 points $\mathbf{B}_{1}, \mathbf{B}_{2}, \mathbf{B}_{3}, \mathbf{B}_{4}, \mathbf{B}_{5}, \mathbf{B}_{6}$ and $\mathrm{B}_{7}$ on $\mathrm{AX}$, such that $\mathrm{AB}_{1}=\mathrm{B}_{1} \mathrm{~B}_{2}=\mathrm{B}_{2} \mathrm{~B}_{3}=\mathrm{B}_{3} \mathrm{~B}_{4}=\mathrm{B}_{4} \mathrm{~B}_{5}=\mathrm{B}_{5} \mathrm{~B}_{6}=\mathrm{B}_{6} \mathrm{~B}_{7}$

6. Join $\mathrm{B}_{7} \mathrm{~B}$ and from $\mathrm{B}_{5}$ draw $\mathrm{B}_{5} \mathrm{M}$ ||  $\mathrm{B}_{7} \mathrm{~B}$ intersecting $\mathrm{AB}$ at $\mathrm{M}$.

7. From point  ${\text{M}}$  draw  ${\text{MN}}\parallel {\text{BC}}$  intersecting  ${\text{AC}}$  at  ${\text{N}}$ . Then,  ${\text{\Delta AMN}}$  is the required triangle whose sides are equal to  $\dfrac{5}{7}$  of the corresponding sides of the $\vartriangle {\text{ABC}}$ .

Justification:

Here,  ${{\text{B}}_{\text{5}}}{\text{M}}\parallel {{\text{B}}_{\text{7}}}{\text{B}}$  (by construction) 

$\therefore \quad \dfrac{{{\text{AM}}}}{{{\text{MB}}}}{\text{ = }}\dfrac{{\text{5}}}{{\text{2}}}$  

$\Rightarrow \dfrac{{{\text{MB}}}}{{{\text{AM}}}}{\text{ = }}\dfrac{{\text{2}}}{{\text{5}}}$  

Now

$\dfrac{{{\text{AB}}}}{{{\text{AM}}}}{\text{ = }}\dfrac{{{\text{AM + MB}}}}{{{\text{AM}}}}$  

${\text{ = 1 + }}\dfrac{{{\text{MB}}}}{{{\text{AM}}}}$  

${\text{ = 1 + }}\dfrac{{\text{2}}}{{\text{5}}}$  

${\text{ = }}\dfrac{{\text{7}}}{{\text{5}}}$  

Also,  $\quad {\text{MN}}\parallel {\text{BC}}$ 

$\therefore \quad \Delta {\text{AMN}}$ proportinate to $\Delta {\text{ABC}}$ 

Therefore,  $\dfrac{{{\text{AM}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{AN}}}}{{{\text{AC}}}}{\text{ = }}\dfrac{{{\text{NM}}}}{{{\text{BC}}}}{\text{ = }}\dfrac{{\text{5}}}{{\text{7}}}$ .

6. Draw a circle of radius $4cm$. Construct a pair of tangents to it, the angle between which is $6{0^\circ }$. Also, justify the construction. Measure the distance between the center of the circle and the point of intersection of tangents. In order to draw the pair of tangents, we follow the following steps

Ans:

Steps of construction:

1. Take a point  ${\text{O}}$  on the plane of the paper and draw a circle of radius  ${\text{OA  =  4cm}}$ .

2. Produce  ${\text{OA}}$  to  ${\text{B}}$  such that  ${\text{OA  = AB  =  4cm}}$ .

3. Taking  ${\text{A}}$  as the centre draw a circle of radius  ${\text{AO}} = {\text{AB}} = 4{\text{cm}}$ . Suppose it cuts the circle drawn in step 1 at  ${\text{P}}$  and  ${\text{Q}}$ .

4. Join  ${\text{BP}}$  and  ${\text{BQ}}$  to get desired tangents.

Justification:

In  $\delta {\text{OAP}}$ , we have

${\text{OA  =  OP  =  4cm}}$  (Radius)

Also,  ${\text{AP  =  4cm}}$ 

$ (\because  $  Radius of circle with centre  ${\text{A)}}$ 

$\therefore \Delta {\text{OAP}}$  is equilateral  $\Rightarrow \angle {\text{PAO}} = {60^\circ } \Rightarrow \angle {\text{BAP}} = {120^\circ }$ 

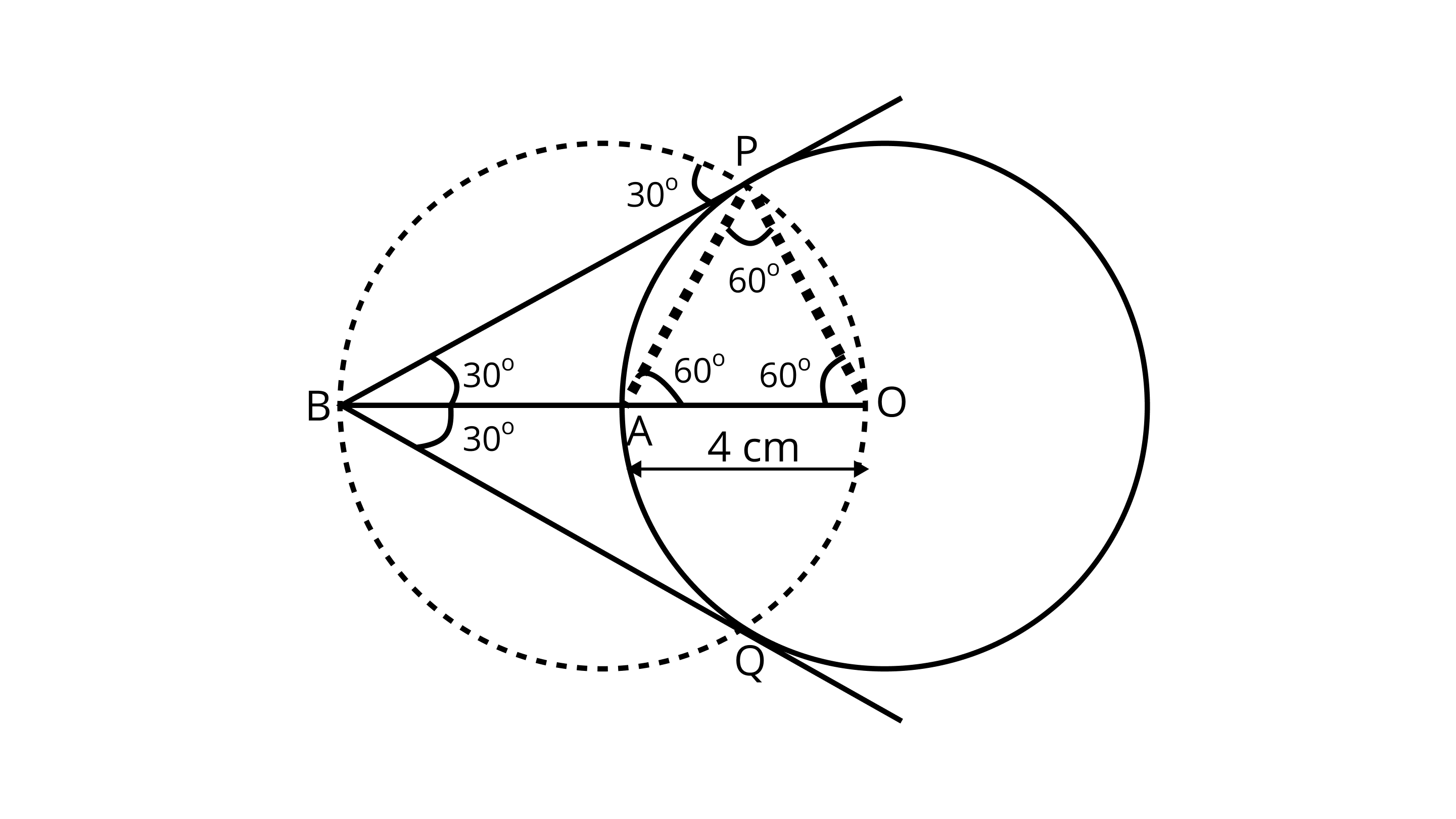
In  $\vartriangle {\text{BAP}}$ , we have

${\text{BA}} = {\text{AP}}$  and  $\angle {\text{BAP}} = {120^\circ }$ 

$\therefore \angle {\text{ABP}} = \angle {\text{APB}} = {30^\circ } \Rightarrow \angle {\text{PBQ}} = {60^\circ }$ 

7. Draw a triangle  $ABC$  in which  $AB  =  4cm, BC  =  6cm$  and  $AC  =  9cm$ . Construct a triangle similar to  $\vartriangle ABC$  with scale factor  $\dfrac{3}{2}$ . Justify the construction. Are the two triangles congruent? Note that all the three angles and two sides of the two triangles are equal.

Ans:

Steps of construction:

1. Draw a line segment ${\text{BC  =  6cm}}$ .

2. Taking  ${\text{B}}$  and  ${\text{C}}$  as centres, draw two arcs of radii  ${\text{4cm}}$  and  ${\text{9cm}}$  intersecting each other at  ${\text{A}}$ 

3. Join  ${\text{BA}}$  and  ${\text{CA}}$ .  

$\delta {\text{ABC}}$  is the required triangle.

4. From  ${\text{B}}$ , draw any ray  ${\text{BX}}$  downwards making an acute angle  $\angle {\text{CBX}}$ 

5. Mark three points ${{\text{B}}_1},{{\text{B}}_2},{{\text{B}}_3}$ , on ${\text{BX}}$ , such that ${\text{B}}{{\text{B}}_1} = {{\text{B}}_1}{{\text{B}}_2} = {{\text{B}}_2}{{\text{B}}_3}$ .

6. Join  ${{\text{B}}_2}{\text{C}}$  and from  ${{\text{B}}_3}$  draw  ${{\text{B}}_3}{\text{M}}\parallel {{\text{B}}_2}{\text{C}}$  intersecting  ${\text{BC}}$  at  ${\text{M}}$ 

7. From point ${\text{M}}$ , draw  ${\text{MN}}\parallel {\text{CA}}$  intersecting the extended line segment  ${\text{BA}}$  to ${\text{N}}$ . Then  $\delta {\text{NBM}}$  is the required triangle whose sides are equal to  $\dfrac{3}{2}$  of the $\vartriangle {\text{ABC}}$ .

Justification:

Here,  ${{\text{B}}_{\text{3}}}{\text{M}}\parallel {{\text{B}}_{\text{2}}}{\text{C}}$ 

\[\therefore \quad \dfrac{{{\text{BC}}}}{{{\text{CM}}}} = \dfrac{2}{1}\]

Now,

$\dfrac{{{\text{BM}}}}{{{\text{BC}}}} = \dfrac{{{\text{BC + CM}}}}{{{\text{BC}}}}$

$= 1 + \dfrac{{{\text{CM}}}}{{{\text{BC}}}}$ 

$= 1 + \dfrac{1}{2}$ 

$= \dfrac{3}{2}$  

Also,  ${\text{MN}}\parallel {\text{CA}}$ 

$\therefore \vartriangle {\text{ABC}}$ proportinate to $\Delta {\text{NBM}}$ 

Therefore,  $\dfrac{{{\text{NB}}}}{{{\text{AB}}}} = \dfrac{{{\text{NM}}}}{{{\text{AC}}}} = \dfrac{{{\text{BM}}}}{{{\text{BC}}}} = \dfrac{3}{2}$ 

The two triangles are not congruent because, if two triangles are congruent, then they have same shape and same size. Here, all the three angles are same but three sides are not same i.e., one side is different.

Importance of Class 10 Mathematics Chapter 10 Syllabus

Class 10 is the first face-off for a student as they will appear for the first time in their board’s examination. Students practice to their extent to attain a good percentage in the examinations. Each subject has its importance but the hype created for maths is unbelievable. Each chapter is important to score good marks in the examinations. NCERT exemplar for Class 10 Maths Chapter 10 - Construction is available on Vedantu’s official website. Students can download the PDF from Vedantu.com. 

This PDF consists of question examples that help a student to practice more and more for their exams. The PDF is prepared from the latest pattern of the CBSE Board, with the latest question pattern. Every question is solved by the faculty of Vedantu itself and has a full explanation step by step for a better understanding of students. Students can practice the given questions and can achieve good scores in their exams. Students following these Exemplars will stay ahead in the class, as it is a fantastic study tool. 

The exemplar given in the PDF are the problems and solutions that are specially designed by the expert faculty of Vedantu concerning the CBSE syllabus, which consists of the following topics - 

1. Division of a line segment in the given ratio

2. Construction of triangle

3. Construction of tangents to a circle

The chapter explains the construction concepts for the students that they have to learn and master. This chapter is a crucial part of geometry as students have to develop mathematical reasoning for the construction of angles.

Benefits of Using Class 10 Chapter 10 Maths solutions from Vedantu

To help students to understand the concepts of construction and make them familiar with the problem-solving methods, free NCERT exemplars are available on the Vedantu website. To help the students Vedantu also provides online reading material like exemplar books, notes, NCERT maths textbook solutions, NCERT Class 10 question papers. They recommend students to practice more and more by solving the question papers on the chapter Construction.

Vedantu also provides personalized videos for the chapter construction so that students can learn with the live classes. Students also can clear their doubts through the session. Students must register themselves at the registered forum of Vedantu so that they get the day-to-day notification of the emails. This method will make them consistent for the Classes and can revise the concepts easily. Students also get preparation tips for their preparation and a study plan that has a specialized study pattern. 

Why wait then? Download the solution file for this chapter and complete preparing it in the best way possible. Clarify your doubts using the conceptual solutions given for all the exercise problems available at Vedantu. Learn how to approach different types of problems and save your time. Use the wisdom shared by the top subject experts to build a strategy before appearing in the board exam. Proceed to the next chapters by downloading the solutions files from here.

Significance of CBSE Class 10 Chapter 10 Constructions NCERT Exemplar Solutions

The chapter needs proper practice and the support of good study material. In this aspect, students often solve the NCERT Exemplar exercises to take a step ahead. Solving these exercises will imbibe the concepts well in their minds.

To make the process easier, they can refer to the solutions developed by the experts. These solutions are designed to focus on the CBSE Class 10 standards. Hence, the answers to the fundamental questions will be easily comprehensible.

Following these questions and answers will develop the conceptual foundation for this chapter. To magnify the preparation of the students, the NCERT Exemplar exercises and the solutions will be a mandatory part of the practice material.

Advantages of CBSE Class 10 Chapter 10 Constructions NCERT Exemplar Solutions

• The solutions have been framed in a simpler tone to offer an easier medium for understanding how to use the concepts and principles of constructions in solving problems.

• The solutions will aid you to resolve doubts on your own. You can use these solutions to overcome the hurdles by clarifying doubts and resolving queries.

• Find out how the experts have framed the answers. The stepwise methods of construction will teach you how to approach a particular problem. By following and practising these methods, you can develop your answering skills accordingly.

• Check your preparation level by comparing your answers to the solutions and find out which part of the chapter needs more attention from your end.