NCERT Exemplar for Class 11 Physics Chapter 13 - Kinetic Theory (Book Solutions)

1. A cubic vessel (with faces horizontal + vertical) contains an ideal gas at NTP. The vessel is being carried by a rocket which is moving at a speed of \[{{500m}}{{{s}}^{ - 1}}\] in vertical direction. The pressure of the gas inside the vessel as observed by us on the ground 

(a) remains the same because \[{{500m}}{{{s}}^{ - {{1}}}}\] is very much smaller than ${V_{rms}}$ of the gas. 

(b) remains the same because motion of the vessel as a whole does not affect the relative motion of the gas molecules and the walls. 

(c) will increase by a factor equal to $\dfrac{{\left[ {v_{rms}^2 + {{\left( {500} \right)}^2}} \right]}}{{v_{rms}^2}}$ where ${V_{rms}}$ was the original mean square velocity of the gas. 

(d) will be different on the top wall and bottom wall of the vessel.

Ans. option (b) 

The relative speed of molecules with relation to the walls of a container doesn’t convert in a rocket because the mass of a molecule is negligible with relation to the mass of the whole system and the system of gas moves as an entire and $g = 0$ on molecules everywhere. Acceleration of the rocket is additionally zero as a result of the rocket moving with constant speed. Thus, the pressure inside the vessel of gas as perceived by us on the bottom remains the same. So, option (b) is correct.

2. \[{{1}}{\text{ }}{{mole}}\] of an ideal gas is contained in a cubical volume\[{{V}}\], \[{{ABCDEFGH}}\] at \[{{300}}{\text{ }}{{K}}\] (Figure). One face of the cube \[\left( {{{EFGH}}} \right)\] is made up of a material which totally absorbs any gas molecule incident on it. At any given time, Exercise

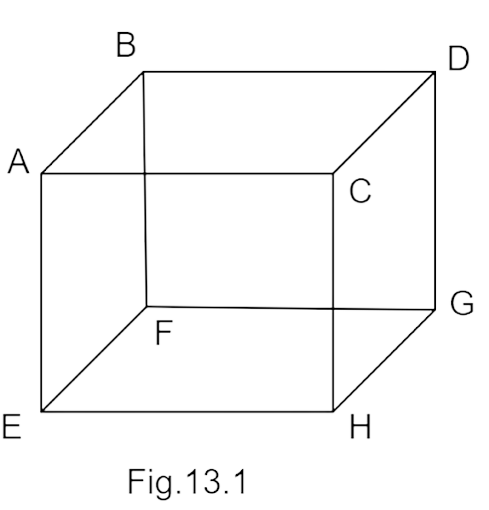
(a) the pressure on \[{{EFGH}}\] would be zero. 

(b) the pressure on all the faces will be equal. 

(c) the pressure of \[{{EFGH}}\] would be double the pressure on\[{{ABCD}}\]. 

(d) the pressure on \[{{EFGH}}\] would be half that on\[{{ABCD}}\].

Ans. option (d) 

The wall experienced pressure due to the force exerted by molecules on walls because of its rate of transfer of momentum to the wall. Due to elastic collision and magnitude of momentum transferred to the wall by each molecule is $2\;mv$ but wall $EFGH$ absorbs those molecules which strike on it. Therefore, the rate of change in momentum to it becomes only $mv$ so the pressure of $EFGH$ would be half of $ABCD.$ Thus, option (d) is correct.

3. Boyle’s law is applicable for an 

(a) adiabatic process 

(b) isothermal process 

(c) isobaric process 

(d) isochoric process

Ans. option (b) 

We know that Boyle’s law is relevant at constant temperature and the temperature remains constant in isothermal processes.

$PV = nRT$ ($n$,$R$ and $T$ are constant)

$\therefore PV = constant{\text{ }}$

$P \propto \dfrac{1}{V}$(Where \[constant = nRT\])

Thus, option (b) is correct.

4. A cylinder containing an ideal gas is in vertical position and has a piston of mass \[{{M}}\]that is able to move up or down without friction (Fig. 13.2). If the temperature is increased, 

(a) both \[{{p}}\] and \[\;{{V}}\]of the gas will change. 

(b) only \[{{p}}\] will increase according to Charles law. 

(c) \[\;{{V}}\] will change but not \[{{p}}\]. 

(d) \[{{p}}\] will change but not \[\;{{V}}\].

Ans. Option (c) 

On the ideal gas, the pressure exerted does not convert from initial to final position. According to the given arrangement $P = \dfrac{{Mg}}{A}$ which shows that pressure is constant. As piston and cylinder are frictionless thus by ideal gas equation 

$PV = nRT$

Where $P$, $n$ and $R$ is constants thus,

$V \propto T$

Thus, on increasing the temperature of the system, it’s volume will increase but $P$ will remain constant.

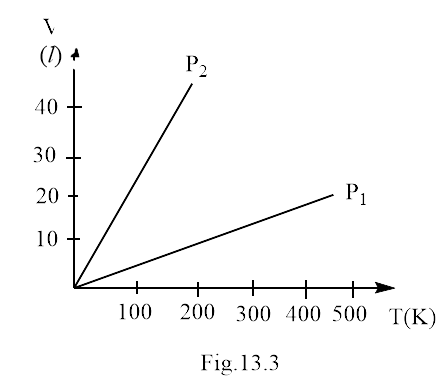
5. Volume versus temperature graphs for a given mass of an ideal gas are shown in Fig. 13.3 at two different values of constant pressure. What can be inferred about the relation between ${P_1}$ and ${P_2}$?

(a) ${P_1} > {P_2}$ 

(b) ${P_1} = {P_2}$

(c) ${P_1} < {P_2}$ 

(d) data is insufficient 

Ans. option (a)

As we know that the pressure and the quantity of gas in the system are constants. Thus, by using ideal gas equation 

$PV = nRT$

$V \propto T$ (When $n$,$P$ and $R$ are constants)

$\dfrac{{{V_1}}}{{{T_1}}} = constant$

Or slope of graph is constant

$V = \dfrac{{nRT}}{P}$

$\dfrac{{dV}}{{dT}} = \dfrac{{nR}}{P}$

or $\dfrac{{dV}}{{dT}}$ increases when $P$ decreases

thus, 

$\dfrac{{dV}}{{dT}} \propto \dfrac{1}{p}$

This shows that slope ${p_1}$ is smaller than ${p_2}$. Thus, this verifies option (a).

6. \[{{1}}\]mole of ${H_2}$ gas is contained in a box of volume $V = 1.00\;{m^3}$at$T = 300\,K$. The gas is heated to a temperature of $T = 3000\;K$ and the gas gets converted to a gas of hydrogen atoms. The final pressure would be (considering all gases to be ideal) 

(a) same as the pressure initially. 

(b) \[{{2}}\] times the pressure initially. 

(c) \[{{10}}\] times the pressure initially. 

(d) \[{{20}}\] times the pressure initially

Ans. option (c) 

Because of the rate of change of momentum $\left( p \right)$, pressure exerted by gas imparted by the particle to the wall. The momentum depends upon mass $'m'$ and velocity $'u'$ of the particle. When at high temperature ${H_2}$ molecules break up into atoms then because the velocity of a gas molecule depends only on temperature, the number of particles becomes double but mass becomes half. Thus, the velocity of the ${H_2}$ molecule and $H$ atom at $3000\;K$ remains the same.

Let the speed of the ${H_2}$ molecule be $'u'$ and the mass of each atom be $'{m_H}'$. So, momentum imparted becomes

$2\left( {2{m_H}} \right)u = 4{m_H}u$

Thus, pressure does not change due to change into atomic form at same temperature

But 

$u \propto T$

$ \Rightarrow P \propto T$

$\therefore \dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{{T_2}}}{{{T_1}}}$

$ \Rightarrow \dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{3000}}{{300}}$

${P_2} = 10{P_1}$

Thus, pressure must be $10$ times. By law of conservation, $p$ does not change at the same temperature. Thus, this verifies option (c) not (d).

7. A vessel of volume \[{{V}}\] contains a mixture of \[{{1}}\] mole of Hydrogen and \[{{1}}\] mole of Oxygen (both considered as ideal). Let ${f_1}\left( v \right)dv$, denote the fraction of molecules with speed between \[{{v}}\]and $\left( {v + dv} \right)$with ${f_2}\left( v \right)dv$, similarly for oxygen. Then 

(a) ${f_1}\left( v \right) + {f_2}\left( v \right) = f\left( v \right)$ obeys Maxwell's distribution law. 

(b) ${f_1}\left( v \right)$, ${f_2}\left( v \right)$ will obey Maxwell's distribution law separately. 

(c) Neither ${f_1}\left( v \right)$, nor ${f_2}\left( v \right)$ will obey Maxwell's distribution law. 

(d) ${f_2}\left( v \right)$ and ${f_1}\left( v \right)$ will be the same.

Ans.  Option (b) 

The number of molecules $n$ for the function ${f_1}\left( v \right)$ will have their speed $\left( {v + dv} \right).$

For ${f_1}\left( v \right)$ and ${f_2}\left( v \right)$

Number of molecules for ${f_1}\left( v \right)$ and ${f_2}\left( v \right)$ remains same ( $1$ mole each) but because of mass difference their speed will be dissimilar, thus both gases will obey the Maxwell’s distribution law separately. 

8. An inflated rubber balloon contains one mole of an ideal gas, has a pressure\[{{p}}\], volume \[{{V}}\] and temperature\[\;{{T}}\]. If the temperature rises to $1.1\;T$, and the volume is increased to$1.05\;V$, the final pressure will be 

(a)$1.1\;p$ 

(b) \[{{p}}\]

(c) less than \[{{p}}\] 

(d) between \[{{p}}\] and \[{{1}}.{{1}}\]

Ans. option (d) 

According to ideal gas equation 

$PV = nRT$

Where $n$ and $R$ are constant for the system here 

So, $\dfrac{{PV}}{T} = constant$

Or $\dfrac{{{P_1}{V_1}}}{{{T_1}}} = \dfrac{{{P_2}{V_2}}}{{{T_2}}}$

${P_2} = \dfrac{{{P_1}{V_1}}}{{{T_1}}} \times \dfrac{{{T_2}}}{{{V_2}}}$

$ = \dfrac{{p \times V \times 1.1 \times T}}{{T \times 1.05 \times V}}$

$ = \dfrac{{1.1}}{{1.05}}p$

$ = \left( {1.0476} \right)p$

i.e.,${P_2}$ is between $p$ and $1.1\;p$. Thus, option (d) is correct.

MULTIPLE CHOICE QUESTIONS-II

9. ABCDEFGH is a hollow cube made of an insulator (Fig. 13.4). Face ABCD has a positive charge on it. Inside the cube, we have ionized hydrogen. The usual kinetic theory expression for pressure 

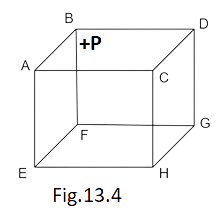
(a) will be valid. 

(b) will not be valid since the ions would experience forces other than due to collisions with the walls. 

(c) will not be valid since collisions with walls would not be elastic. 

(d) will not be valid because isotropy is lost.

Ans. options (b) and (d) 

There will be electrostatic force due to the pressure of hydrogen ions and positive charged wall ABCD which acts a part of collision, thus Kinetic theory of gas is not applicable. The isotropy also vanishes because of the appearance of ions in place of hydrogen molecules. So, options (b) and (d) are correct.

10. Diatomic molecules like hydrogen have energies due to both translational as well as rotational motion. From the equation in kinetic theory $pV = \dfrac{2}{3}E$, $E$ is

(a) the total energy per unit volume. 

(b) only the translational part of energy because rotational energy is very small compared to the translational energy. 

(c) only the translational part of the energy because during collisions with the wall pressure relates to change in linear momentum. 

(d) the translational part of the energy because rotational energies of molecules can be of either sign and its average over all the molecules is zero.

Ans. option (c) 

The postulate of kinetic theory of gases state that it is assumed that pressure created by gas molecules is because of the perpendicular forces only exerted by molecules on the wall during the motion of molecules, i.e., the molecule striking at any other angle except ${90^ \circ }$ will not exert pressure. Thus, because of change in translational motion, pressure exerted on the wall. Hence, $PV = \dfrac{2}{3}E$ represents only the translation part of energy. So, option (c) is correct.

11. In a diatomic molecule, the rotational energy at a given temperature 

(a) obeys Maxwell’s distribution. 

(b) have the same value for all molecules. 

(c) equals the translational kinetic energy for each molecule. 

(d) is $\left( {\dfrac{2}{3}} \right)rd$ the translational kinetic energy for each molecule.

Ans. option (a) and option (d) 

Let us suppose a diatomic molecule along \[z - axis\] thus, the rotational energy of a diatomic molecule about $z - axis$ will be zero. Therefore, energy of diatomic molecule 

$E = \dfrac{1}{2}mv_x^2 + \dfrac{1}{2}mv_y^2 + \dfrac{1}{2}mv_z^2 + \dfrac{1}{2}{I_x}w_x^2 + \dfrac{1}{2}{I_y}w_y^2$

$\because $ along $z - axis$, moment of inertia is zero.

The individualistic terms given in the above expression is $5$. Because of Maxwell’s distribution, we can previse velocities of molecules. Thus, this means that the above expression also follows Maxwell’s distribution. $2$ rotational and $3$ translational energies are analogous with each molecule. Thus, at the given temperature, the rotational energy is $\dfrac{2}{3}$ of its translational Kinetic energy of each molecule. Thus, option (a) and option (d) are correct.

12. Which of the following diagrams (Fig. 13.5) depicts ideal gas behaviour? 

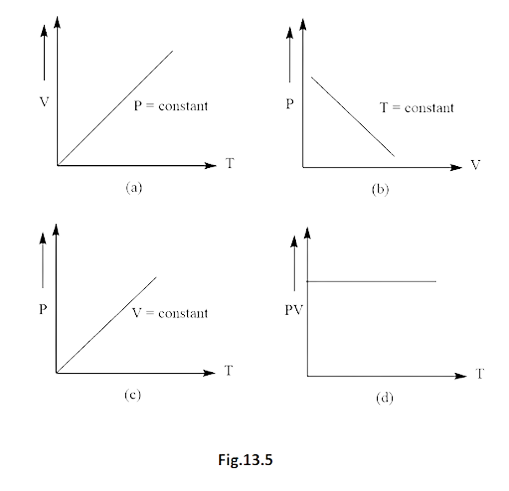
Ans.  options (a) and (c)

The gas equation for ideal gas is

$PV = nRT$

Where, $n$ and $R$ are constants for the system

(a) When $P$ is constant

Then,

$V \propto T$

Thus diagram (a) verified.

(b) When $T$ is constant

Then, $PV = constant$

Which means that graph should be parabola (Rectangular).

Hence, does not verify diagram (b).

(c) When $V$ is constant

$P \propto T$

Which is the straight line 

Thus, diagram (c) verified.

When $\dfrac{{PV}}{T}$ (slope) is constant

At $P = 0$,

\[constant\;K = 0\]

And at $V = 0$, 

\[constant\;K = 0\]

Thus, the graph should pass through origin. But not in diagram (d). Hence does not verify diagram (d).

13. When an ideal gas is compressed adiabatically, its temperature rises: the molecules on the average have more kinetic energy than before. The kinetic energy increases, 

(a) because of collisions with moving parts of the wall only. 

(b) because of collisions with the entire wall. 

(c) because the molecules get accelerated in their motion inside the volume. 

(d) because of redistribution of energy amongst the molecules.

Ans.  Option (a)

The mean free path becomes smaller because the ideal gas constricts, thus escalating the number of collisions per second among the molecules and walls. Because of which the temperature of gas increases which in turn escalates the Kinetic energy of gas molecules. Kinetic energy relies on temperature.

VERY SHORT ANSWER TYPE QUESTIONS

14. Calculate the number of atoms in $39.4\,g$ gold. Molar mass of gold is$197\,g\,\;mol{e^{ - 1}}$.

Ans. Quantity of atoms in $197\;gm$ of gold $ = 6.023 \times {10^{23}}$

Quantity of atoms in $1\;gm$ of gold $ = \dfrac{{6.023 \times {{10}^{23}}}}{{197}}$

Number of atoms in $39.4\;gm$ of gold $ = \dfrac{{39.4 \times 6.023{\kern 1pt}  \times {{10}^{23}}}}{{197}}$

$ = 1.2 \times {10^{23}}\;atoms.$

15. The volume of a given mass of a gas at\[{{27}}^\circ {{C}}\], \[{{1}}{\text{ }}{{atm}}\]is \[{{100}}{\text{ }}{{cc}}\]. What will be its volume at ${327^ \circ }C$?

Ans.  According to the gas equation of ideal gas 

${P_1} = 1\,atm$, ${P_2} = 1\;atm$, ${V_1} = 100\,cc$, ${V_2} = ?$

${T_1} = 273 + 27 = 300\;K$, ${T_2} = 327 + 273 = 600\;K$

$\therefore \dfrac{{{P_1}{V_1}}}{{{T_1}}} = \dfrac{{{P_2}{V_2}}}{{{T_2}}}$

$\dfrac{{1 \times 100}}{{300}} = \dfrac{{1 \times {V_2}}}{{600}}$

$ \Rightarrow {V_2} = \dfrac{{100 \times 600}}{{300}}$

$ = 200\;cc$

Here we can use units of pressure and volume differently but for temperature it should be the same.

16. The molecules of a given mass of a gas have root mean square speeds of $100\,m\,{s^{ - 1}}$ at \[{{27}}{\text{ }}{{C}}^\circ \] and \[{{1}}.{{00}}\] atmospheric pressure. What will be the root mean square speeds of the molecules of the gas at 127°C and \[{{2}}.{{0}}\] atmospheric pressure?

Ans. ${v_{1\;rms}} = 100\,m{s^{ - 1}}$

${T_1} = 27 + 273 = 300\;K$

Then ${v_{2\;rms}} = ?$

${T_2} = 127 + 273 = 400\;K$

${v_{rms}} = \sqrt {\dfrac{{3RT}}{M}} $

Where $M = $ Molar mass of gas for a gas $M$ is constant.

$\therefore {v_{rms}} \propto \sqrt T $

$\dfrac{{{v_{1\;rms}}}}{{{v_{2\;rms}}}} = \sqrt {\dfrac{{{T_1}}}{{{T_2}}}} $

$\dfrac{{100}}{{{v_{2\,rms}}}} = \sqrt {\dfrac{{300}}{{400}}} $

${v_{2\,\,rms}} = \dfrac{{100 \times \sqrt {400} }}{{\sqrt {300} }}$

$ = \dfrac{{100 \times 2 \times 10}}{{10\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}$

$ = \dfrac{{200 \times \sqrt 3 }}{3}$

$ = \dfrac{{200 \times 1.732}}{3}$

${v_{2\;rms}} = 115.4\,m{s^{ - 1}}$

17. Two molecules of a gas have speeds of $9 \times {10^6}\,m\,{s^{ - 1}}$and$1 \times {10^6}\,m\;{s^{ - 1}}$, respectively. What is the root mean square speed of these molecules?

Ans.  ${v_{rms}} = \sqrt {\dfrac{{v_1^2 + v_2^2 + ..... + v_n^2}}{n}} $ 

$\left( where,\,{v_1} = 9 \times {10^6}\;m{s^{ - 1}}, {v_2} = 1 \times {10^6}\;m{s^{ - 1}} \right)$

$\therefore {v_{rms}} = \sqrt {\dfrac{{{{\left( {9 \times {{10}^6}} \right)}^2} + {{\left( {1 \times {{10}^6}} \right)}^2}}}{2}} $

${v_{rms}} = \sqrt {\dfrac{{81 \times {{10}^{12}} + 1 \times {{10}^{12}}}}{2}} $

$ = \sqrt {\dfrac{{{{10}^{12}}\left( {81 + 1} \right)}}{2}} $

$ = {10^6}\sqrt {\dfrac{{82}}{2}} $

$ = {10^6}\sqrt {41} $

$ = {10^6} \times 6.4$

${v_{rms}} = 6.4 \times {10^6}m{s^{ - 1}}$

18. A gas mixture consists of \[{{2}}.{{0}}\] moles of oxygen and \[{{4}}.{{0}}\] moles of neon at temperature\[{{T}}\]. Neglecting all vibrational modes, calculate the total internal energy of the system. (Oxygen has two rotational modes.)

Ans. For finding the total energy of the given molecule of the gas, we should find its degree of freedom. The molecule of oxygen has $2\,atoms$. Thus, the degree of freedom of it is $3T + 2R = 5$, so total internal energy is 

$ = \dfrac{5}{2}RT$ per mole as gas ${O_2}$ is $2$ mole

Thus, total internal energy of $2$ mole oxygen $ = \dfrac{{2 \times 5}}{2}RT$$ = 5RT$

We know that Neon gas is monatomic so its degree of freedom is only $3$ hence total internal energy $ = \dfrac{3}{2}RT\,per\,mole$

Thus, total internal energy of $4$ mole of$Ne$$ = \dfrac{{4 \times 3}}{2}RT$$ = 6RT$

Total internal energy of \[2\] mole oxygen and $4$ mole $Ne$ $ = 5RT + 6RT$

$ = 11RT$

19. Calculate the ratio of the mean free paths of the molecules of two gases having molecular diameters \[{{1A}}\] and\[{{2}}{\text{ }}{{A}}\]. The gases may be considered under identical conditions of temperature, pressure and volume.

Ans. Mean free path

$\lambda  = \dfrac{1}{{\sqrt 2 \pi {d^2}n}}$

Where, $n = \;number\,of\;molecules\,per\;unit\,volume$, $d = diameter\,of\,molecule$

Because the condition for both gases are identical so $n$ will be constant 

Or $\lambda  \propto \dfrac{1}{{{d^2}}}$

Or $\dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \dfrac{{d_2^2}}{{d_1^2}} = \dfrac{{{{\left( 2 \right)}^2}}}{{{{\left( 1 \right)}^2}}}$

${\lambda _1} :{\lambda _2} = 4:1$

SHORT ANSWER TYPE QUESTIONS

20. The container shown in Figure has two chambers, separated by a partition, of volumes ${V_1} = 2.0L$ and ${V_2} = 3.0\,L$. The chambers contain \[{\mu _1} = {\text{ }}{{4}}.{{0}}\] and \[{\mu _2}{\text{ }} = {\text{ }}{{5}}.{{0}}\] moles of a gas at pressures \[{{\text{P}}_1}{\text{ }} = {\text{ }}{{1}}.{{00}}{\text{ }}{{atm}}\] and \[{P_2} = {\text{ }}{{2}}.{{00}}{\text{ }}{{atm}}\]. Calculate the pressure after the partition is removed and the mixture attains equilibrium.

Ans. According to ideal gas equation

$PV = \mu RT$

The gases in chamber $1\;$ and $2$

${P_1}{V_1} = {\mu _1}R{T_1}$

${P_2}{V_2} = {\mu _2}R{T_2}$

${P_1} = 1\;atm$, ${P_2} = 2\;atm$

${V_1} = 2\;L$, ${V_2} = 3\;L$

${T_1} = T$, ${T_2} = T$

${\mu _1} = 4$, ${\mu _2} = 5$

When we remove the partition between gases then

$\mu  = {\mu _1} + {\mu _2}$ and $V = {V_1} + {V_2}$

According to the kinetic theory of gases 

The kinetic translational energy 

$ = PV = \dfrac{2}{3}E$ per mole

Thus, kinetic translational energy by the gas of ${\mu _1}$ moles

${P_1}{V_1} = \dfrac{2}{3}{\mu _1}{E_1}$

And ${P_2}{V_2} = \dfrac{2}{3}{\mu _2}{E_2}$

Adding both above 

${P_1}{V_1} + {P_2}{V_2} = \dfrac{2}{3}{\mu _1}{E_1} + \dfrac{2}{3}{\mu _2}{E_2}$

Or ${\mu _1}{E_1} + {\mu _2}{E_2} = \dfrac{3}{2}\left( {{P_1}{V_1} + {P_2}{V_2}} \right)$

Combined effect,

$PV = \dfrac{2}{3}{E_{total}}$ per mole $ = \dfrac{3}{2}\mu E$ per mole

$P\left( {{V_1} + {V_2}} \right) = \dfrac{2}{3}\left[ {\dfrac{3}{2}\left( {{P_1}{V_1} + {P_2}{V_2}} \right)} \right]$

$P = \dfrac{{\left( {{P_1}{V_1} + {P_2}{V_2}} \right)}}{{\left( {{V_1} + {V_2}} \right)}}$

$ = \dfrac{{1.00 \times 1.0 + 2.00 \times 3.0}}{{2.0 + 3.0}}atm$

$P = \dfrac{{2 + 6}}{5}$

$ = \dfrac{8}{5}$

$ = 1.6\,atm$.

21. A gas mixture consists of molecules of types \[{{A}}\], \[{{B}}\] and \[{{C}}\] with masses ${m_A} > {m_B} > {m_C}$ at constant temperature and pressure. Rank the three types of molecules in decreasing order of (a) average \[{{K}}.{{E}}.\] 

Ans. ${v_{av}} = \bar v = \sqrt {\dfrac{{8{K_B}T}}{{\pi m}}} $

$ = \sqrt {\dfrac{{8RT}}{{\pi m}}} $

$ = \sqrt {\dfrac{{8PV}}{{\pi m}}} $

According to the question, because temperature and pressure are same

${v_{av}} = \bar v \propto \dfrac{1}{{\sqrt m }}$

${v_C} > {v_B} > {v_A}$

$\therefore as\;K.E. \propto {v^2}$

And $K.E. \propto m$

Thus, $K.E.$ will be affected by $u$ more than the mass of the atom.

Thus, decreasing order of $K.E.$ of molecules is 

$K.E{._C} > K.E{._B} > K.E{._A}$

(b) rms speeds.

Ans: ${v_{rms}} = \sqrt {\dfrac{{3{K_B}T}}{m}} $

Where $P$,$T$ are constant

$\therefore {a_{rms}} \propto \dfrac{1}{{\sqrt m }}$

${m_A} > {m_B} > {m_C}$(given)

$ \Rightarrow {\left( {{v_{rms}}} \right)_C} > {\left( {{v_{rms}}} \right)_B} > {\left( {{v_{rms}}} \right)_A}$

22. We have \[{{0}}.{{5}}{\text{ }}{{g}}\]of hydrogen gas in a cubic chamber of size \[{{3cm}}\] kept at NTP. The gas in the chamber is compressed keeping the temperature constant till a final pressure of\[{{100}}{\text{ }}{{atm}}\]. Is one justified in assuming the ideal gas law, in the final state? (Hydrogen molecules can be consider as sphere of radius $1\mathop {\rm A}\limits^ \circ  $)

Ans. volume of $1$ molecule 

$ = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3} \times 3.14 \times {\left( {{{10}^{ - 10}}} \right)^3}$

[$r = 1\mathop {\rm A}\limits^ \circ  $ (given)]

$\therefore volume\,of\,1\,molecule = 4 \times 1.05 \times {10^{ - 30}}{m^3}$

$ = 4.20 \times {10^{ - 30}}\,{m^3}$

Number of moles in $ = \dfrac{{0.5}}{2}$$ = 0.25\,\,mole$$[\therefore {H_2}\,has\,2\;mole]$

$\therefore volume\,of\,{H_2}molecules\;in\,0.25\,mole$

$ = 0.25 \times 6.023 \times {10^{23}} \times 4.2 \times {10^{ - 30}}\;{m^3}$

$ = 1.05 \times 6.02 \times {10^{23 - 30}}$

$ = 6.324 \times {10^{23 - 30}}$

$ = 6.3 \times {10^{ - 7}}\;{m^3}$

At constant temperature ideal gas,

${P_i}{V_i} = {P_f}{V_f}$

${V_f} = \dfrac{{{P_i}{V_i}}}{{{P_f}}}$

$ = \dfrac{1}{{100}} \times {\left( {3 \times {{10}^{ - 2}}} \right)^3}$$\left[ {\because vol.\;of\,cube\,{V_i} = {{\left( {side} \right)}^3}and\,{P_i} = 1\,atm\,at\,NTP} \right]$

Thus, compressing the volume of the gas of the order of nuclear force of interaction will play the role, as in kinetic theory of gas molecules do not interact with each other thus gas will not obey the ideal gas behaviour.

23. When air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Boyle’s law in this case?

Ans. By Boyle's law; the volume of gas is inversely proportional to pressure at constant temperature which means it is valid only for constant mass of gas. But in this question, air is pumped continuously in the tyre, so the number of moles of air increases which violate Boyle's law.

24. A balloon has\[\;{{5}}.{{0}}{\text{ }}{{g}}\] mole of helium at\[{{7}}^\circ {{C}}\]. Calculate 

(a) the number of atoms of helium in the balloon, 

Ans. For helium gas 

$n = 5\,mole$

$T = 7 + 273 = 280\;K$

(a) $He$ gas consist number of atoms is $5$ mole $ = 5 \times 6.023 \times {10^{23}}\,atoms$

$ = 30.115 \times {10^{23}}\;atoms$

$ = 3.0115 \times {10^{24}}\;atoms$

(b) the total internal energy of the system.

Ans: As $He$ atom is monoatomic so degree of freedom is three, thus Kinetic energy 

$ = \dfrac{3}{2}{K_B}T$ per molecule

$ = \dfrac{3}{2}{K_B}T \times Number\;of\;He\;atom$

$ = \dfrac{3}{2} \times 1.38 \times {10^{ - 23}} \times 280 \times 3.0115 \times {10^{24}}$

Total $E$ of $15$ mole of $He = 1.74 \times {10^4}J$

25. Calculate the number of degrees of freedom of molecules of hydrogen in 1 cc of hydrogen gas at NTP.

Ans. As we know, the hydrogen molecule is diatomic so it contains three translational degrees of freedom and two rotational degrees of freedom.

Thus, total degree of freedom in ${H_2}$ molecule $ = 3 + 2 = 5$

The number of molecules in $1\;cc$

$22.4\;lit = 22400\,cc$

${H_2}$ gas at STP contain $ = 6.023 \times {10^{23}}\,molecules$

$1\,cc$${H_2}$ gas at STP contain $ = \dfrac{{6.023}}{{22400}} \times {10^{23}}\;molecules$

$ = 2.688 \times {10^{19}}$

Thus, total degree of freedom $ = 5 \times 2.688 \times {10^{19}}$

$ = 13.440 \times {10^{19}}$

$ = 1.344 \times {10^{20}}$

26. An insulated container containing monatomic gas of molar mass \[{{m}}\] is moving with a velocity ${v_ \circ }$. If the container is suddenly stopped, find the change in temperature.

Ans. As the gas is monatomic thus, the total degree of freedom is three which will be because of only translational motion.

Thus, if $K.E.$ per molecule =$\dfrac{3}{2}RT$

When there is a stop in an insulated container then its Kinetic energy is transferred to gas molecules in the form of translational $K.E.$. Hence this increases the absolute temperature of the gas 

Assuming it be $\Delta T$ if $n = $ moles of gas

Thus, increase in translational 

\[K.E. = n\dfrac{3}{2}R\Delta T\]

$K.E. = \dfrac{1}{2}\left( {mn} \right)v_ \circ ^2$ [ increased kinetic energy of molecule because of velocity${v_ \circ }$]

$\therefore \dfrac{{mv}}{2}v_ \circ ^2\dfrac{3}{2}nR\Delta T$

$\Delta T = \dfrac{{mnv_ \circ ^2 \times 2}}{{2 \times 3 \times nR}}$

$ = \dfrac{{mv_ \circ ^2}}{{3R}}$

LONG ANSWER TYPE QUESTIONS

27. Explain why 

(a) there is no atmosphere on the moon. 

Ans. (a) Acceleration due to gravity on the moon is $\dfrac{1}{6}th$ of $g$ on earth. Thus, the escape velocity on moon is

${V_{es}} = 2.38\,km{s^{ - 1}}$

$M = mass\;of\,hydrogen$

Because ${H_2}$ is the lightest gas $m = 1.67 \times {10^{ - 24}}kg$

${v_{rms}} = \sqrt {\dfrac{{3{K_B}T}}{m}} $

$ = \sqrt {\dfrac{{3 \times 1.38 \times {{10}^{ - 23}} \times 300}}{{1.67 \times {{10}^{ - 24}}}}} $

$ = 2.72\,km{s^{ - 1}}$

The molecule of air can escape out due to the small gravitational force and ${v_{rms}}$ is greater than escape velocity.

Because the distance of the moon from the sun is roughly equal to that of earth, thus the intensity of energy of the sun reaches to the moon is larger because of the lower density of the atmosphere. Distance between the moon and sun becomes smaller than earth when the moon is towards the sun during its rotation around the earth.

Because of this, the rms speed of molecules increases and some of the molecules can speed up more than escape velocity and so the possibility of escaping out increases. Thus, over a long-time the moon has lost most of its atmosphere. 

(b) there is a fall in temperature with an increase in altitude.

Ans: Because of the kinetic energy of air molecules, the temperature of the atmosphere. Molecules of air rise up because of lower atmospheric pressure at higher altitude so their potential energy increases in turn the kinetic energy decreases resulting in a decrease in temperature. Because of lower pressure at higher altitude the gas expands and gives a cooling effect and thus decreases the temperature.

28. Consider an ideal gas with the following distribution of speeds. 

(i) Calculate ${V_{rms}}$ and hence\[{{T}}\]. \[\left( {{\text{m}}\,{\text{ =  3}}{\text{.0}} \times {\text{1}}{{\text{0}}^{ - 26}}{\text{kg }}} \right)\]

Ans. $v_{rms}^2 = \dfrac{{{n_1}v_1^2 + {n_2}v_2^2 + .... + {n_n}v_n^2}}{{{n_1} + {n_2} + {n_3}.....{n_n}}}$

$v_{rms}^2 = \dfrac{{10 \times {{\left( {200} \right)}^2} + 20{{\left( {400} \right)}^2} + 40{{\left( {600} \right)}^2} + 20{{\left( {800} \right)}^2} + 10{{\left( {1000} \right)}^2}}}{{10 + 20 + 40 + 20 + 10}}$

$v_{rms}^2 = \dfrac{{{{10}^5}\left[ {4 + 32 + 144 + 128 + 100} \right]}}{{100}}$

$ = {10^3}\left[ {408} \right]$

${v_{rms}} = \sqrt {{{10}^4} \times 40.8} $

$ = {10^2} \times 6.39\;m{s^{ - 1}}$

$\dfrac{1}{2}mv_{rms}^2 = \dfrac{3}{2}{K_B}T$

$T = \dfrac{{mv_{rms}^2}}{{3{K_B}}}$

$ = \dfrac{{3 \times {{10}^{ - 26}} \times {{10}^5} \times 4.08}}{{3 \times 1.38 \times {{10}^{ - 23}}}}$

$ = \dfrac{{204 \times {{10}^{ - 23}} \times {{10}^2}}}{{69 \times {{10}^{ - 23}}}}$

$T = 2.96 \times {10^2} = 296\,K$

(ii) If all the molecules with speed \[{\text{1000}}\,{\text{m}}{{\text{s}}^{ - 1}}{\text{ }}\] escape from the system, calculate new ${V_{rms}}$ and hence \[{{T}}\].

Ans: When molecules escape $1000\;m{s^{ - 1}}$ out then,

$v_{rms}^2 = \dfrac{{10 \times {{\left( {200} \right)}^2} + 20 \times {{\left( {400} \right)}^2} + 40 \times {{\left( {600} \right)}^2} + 20 \times {{\left( {800} \right)}^2}}}{{10 + 20 + 40 + 20}}$

$v_{rms}^2 = \dfrac{{{{10}^5}\left[ {4 + 32 + 144 + 128} \right]}}{{90}}$

${v_{rms}} = \sqrt {\dfrac{{{{10}^5}\left[ {308} \right]}}{{90}}} $

$ = \sqrt {\dfrac{{{{10}^4}}}{9} \times 308} $

$ = \dfrac{{100}}{3}\sqrt {308} $

$ = 33.33 \times 17.55 \cong 585\,m{s^{ - 1}}$

$T = \dfrac{1}{3}\dfrac{{mv_{rms}^2}}{{{K_B}}}$

$ = \dfrac{{3 \times {{10}^{ - 26}} \times {{\left( {585} \right)}^2}}}{{3 \times 1.38 \times {{10}^{ - 23}}}}$

$ = \dfrac{{{{\left( {585} \right)}^2}}}{{138}} \times {10^{ - 24 + 23}}$

$T = 4.24 \times {10^{ - 1}} \times 585$

$ = 248.04\,K$

29. Ten small planes are flying at a speed of \[{\text{150 km}}{{\text{h}}^{ - 1}}\] in total darkness in an air space that is $20 \times 20 \times 1.5\;k{m^3}$ in volume. You are in one of the planes, flying at random within this space with no way of knowing where the other planes are. On the average about how long a time will elapse between a near collision with your plane. Assume for this rough computation that a safety region around the plane can be approximated by a sphere of radius $10\;m$.

Ans. we can consider the planes as the motion of molecules in confined space. The distance between the two planes travelled between the collision or just to avoid an accident is time of relaxation for the mean free path $\lambda $.

$time = \dfrac{{distance}}{{speed}}$

$ = \dfrac{\lambda }{v}$

$ = \dfrac{1}{{\sqrt 2 n.\pi {d^2}.v}}$

$N = $ number of particles per unit volume $V = \dfrac{N}{{Volume}}$

$n = \dfrac{{10}}{{20 \times 20{\kern 1pt}  \times 1.5\,K{m^3}}}$

$ = 0.0167\,k{m^{ - 3}}$

$d = 2 \times 10\;m$

$ = 20\,m$

$ = 20 \times {10^{ - 3}}\,km$

$v = 150\,km{h^{ - 1}}$

$\therefore time = \dfrac{1}{{\sqrt 2 n\pi {d^2}v}}$

$ = \dfrac{1}{{1.414 \times 0.0167 \times 3.14 \times 20 \times 20 \times {{10}^{ - 6}} \times 150}}$

$t = \dfrac{{{{10}^6}}}{{4448.8}}$

$ = 225\,hrs$

30. A box of $1.00\;{m^3}$ is filled with nitrogen at $1.5\;atm$at$300\;K$. The box has a hole of an area $0.010\;n{m^2}$. How much time is required for the pressure to reduce by$0.10\;atm$, if the pressure outside is $1\;atm$.

Ans.  Volume of the box ${V_1} = 1\,{m^3}$

Initial pressure ${P_1} = 1.5\,\,atm$

final pressure ${P'_2} = 1.5 - 0.1 = 1.4\,atm$

air pressure outside box ${P_2} = 1\;atm$

Initial temperature ${T_1} = 300\;K$

Final temperature ${T_2} = 300\,K$

$a = area\;of\;hole = 0.01\,m{m^2}$

$ = 0.01 \times {10^{ - 6}}{m^2}$

$ = {10^{ - 8}}{m^2}$

initial pressure difference between atmosphere and tyre 

$\Delta P = \left( {1.5 - 1} \right)\,atm$

mass of a ${N_2}$ gas molecule $ = \dfrac{{0.028\;Kg}}{{6.023 \times {{10}^{23}}}}$

$ = 46.5 \times {10^{ - 27}}Kg$

${K_B} = 1.38 \times {10^{ - 23}}$

Assuming ${\rho _{in}}$ be the initial number of ${N_2}$ gas molecule per unit volume at time $\Delta t$ and also ${v_{ix}}$be the speed of molecules along $x - axis$

At time $\Delta t$, number of molecules colliding to opposite wall

$\dfrac{1}{2}{\rho _{in}}\left[ {\left( {{v_{ix}}} \right)\Delta t} \right]A$

Half is multiple as half molecule will strike to opposite wall

$v_{rms}^2\left( {{N_2}\,molecule} \right) = v_{ix}^2 + v_{iy}^2 + v_{iz}^2$

$\therefore \left| {{v_{ix}}} \right| = \left| {{v_{iy}}} \right| = \left| {{v_{iz}}} \right|$

Thus, $v_{rms}^2 = 3v_{ix}^2$

$K.E.$ of gas molecule $ = \dfrac{3}{2}{K_B}T$

$\dfrac{1}{2}mv_{rms}^2 = \dfrac{3}{2}{K_B}T$

$m3v_{ix}^2 = 3{K_B}T$

${v_{ix}} = \sqrt {\dfrac{{{K_B}T}}{m}} ...(A)$

At time $\Delta t$, the number of ${N_2}$ gas molecule striking to a wall outward$ = \dfrac{1}{2}{\rho _{in}}\sqrt {\dfrac{{{K_B}T}}{m}} \Delta t \cdot a$

Temperature inside the air and box are equal to $T$

At time $\Delta t$, the number of air molecule striking to hole 

$inward = \dfrac{1}{2}{\rho _{n2}}\sqrt {\dfrac{{{K_B}T}}{m}} \Delta t \cdot a$

Total number of molecules going out from hole at time $\Delta t$

$ = \dfrac{1}{2}\left[ {{\rho _{n1}} - {\rho _{n2}}} \right]\sqrt {\dfrac{{{K_B}T}}{m}} \, \cdot \Delta t \cdot a\,(I)$

Gas equation

${P_1}V = \mu RT$

$ \Rightarrow \mu  = \dfrac{{{P_1}V}}{{RT}}$

For box,

$\dfrac{\mu }{V} = \dfrac{{{P_1}}}{{RT}}$ Where $\mu $= number of moles of gas in box

${\rho _{n1}} = \dfrac{{N\left( {Total\,no.\,of\,molecule\,in\,box} \right)}}{{volume\,of\,box}} = \dfrac{{\mu {N_A}}}{V}$

$ = \dfrac{{{P_1}{N_A}}}{{RT}}$ per unit volume

Assuming after time $T$ pressure reduced by $0.1$ and becomes

$\left( {1.5 - 0.1} \right) = 1.4\,atm\,{P'_2}$

Thus, new final density of ${N_A}$ molecule ${\rho '_{n1}}$

${\rho '_{n1}} = \dfrac{{{P_2}{N_A}}}{{RT}}$ per unit volume (III)

Thus, total number of molecules going out from volume $V$

$ = \left( {{\rho _{n1}} - {{\rho '}_{n1}}} \right)v$

$ = \dfrac{{{P_1}{N_A}}}{{RT}}v - \dfrac{{{{P'}_2}{N_A}}}{{RT}}v$

$ = \dfrac{{{N_A}v}}{{RT}}\left[ {{P_1} - {{P'}_2}} \right]$  (IV) (From II, III)

${P'_2} = $ final pressure of box

Net number of molecules going out in time $\tau $ from hole from (I)

$ = \dfrac{1}{2}\left[ {{\rho _{n1}} - {\rho _{n2}}} \right]\sqrt {\dfrac{{{K_B}T}}{m}} \tau  \cdot a$

${\rho _{n1}} - {\rho _{n2}} = \dfrac{{{P_1}{N_A}}}{{RT}} - \dfrac{{{P_2}{N_A}}}{{RT}}$

$\therefore {\rho _{n1}} - {\rho _{n2}} = \dfrac{{{N_A}}}{{RT}}\left[ {{P_1} - {P_2}} \right]$ (${P_2} = $ Press of air out of box)

In $\tau $ time total number of molecules going out from above

$ = \dfrac{1}{2}\dfrac{{{N_a}}}{{RT}}\left[ {{P_1} - {P_2}} \right]\sqrt {\dfrac{{{K_B}T}}{m}}  \cdot \tau  \cdot a$

From (V) and (IV)

$\dfrac{{{N_A}V}}{{RT}}\left( {{P_1} - {{P'}_2}} \right) = \dfrac{1}{2}\dfrac{{{N_A}}}{{RT}}\left( {{P_1} - {P_2}} \right)\sqrt {\dfrac{{{K_B}T}}{m}}  \cdot \tau  \cdot a$

$\tau  = \dfrac{{{N_A}V}}{{RT}}\left( {{P_1} - {{P'}_2}} \right)\dfrac{{2RT}}{{{N_A}}}\dfrac{1}{{\left( {{P_1} - {P_2}} \right)}}\sqrt {\dfrac{m}{{{K_B}T}}}  \cdot \dfrac{1}{a}$

$\tau  = \dfrac{{2\left( {{P_1} - {{P'}_2}} \right)}}{{\left( {{P_1} - {P_2}} \right)}} \cdot \dfrac{V}{a}\sqrt {\dfrac{m}{{{K_A}T}}} $

$ = \dfrac{{2\left[ {1.5 - 1.4} \right]}}{{\left( {1.5 - 1} \right)}}\dfrac{1}{{{{10}^{ - 8}}}}\sqrt {\dfrac{{46.5 \times {{10}^{ - 27}}}}{{1.38 \times {{10}^{ - 23}} \times 300}}} $

$ = \dfrac{{2 \times 0.1}}{{0.5 \times {{10}^{ - 8}}}}\sqrt {\dfrac{{4650 \times {{10}^{ - 27 + 23 - 2}}}}{{138 \times 3}}} $

$ = 0.4 \times {10^{ + 8}}\sqrt {\dfrac{{775 \times {{10}^{ - 6}}}}{{69}}} $

$ = 0.4 \times {10^{ + 8}} \times {10^{ - 3}} \times \sqrt {11.23} $

$ = 0.4 \times {10^5} \times 3.35$

$\tau  = 1.34 \times {10^5}\,\sec $

31. Consider a rectangular block of wood moving with a velocity ${v_o}$ in a gas at temperature \[{{T}}\] and mass density $\rho $. Assume the velocity is along \[{{x}} - {{axis}}\] and the area of cross-section of the block perpendicular to ${v_o}$ is\[{{A}}\]. Show that the drag force on the block is $4\rho A{v_o}\sqrt {\dfrac{{kT}}{m}} $, where \[{{m}}\] is the mass of the gas molecule.

Ans. Assuming ${\rho _m}$ is the number of molecules per unit volume which means it is the density per unit volume.

The velocity of gas molecules

$v = {v_{rms}}$

The gas molecules strike to the front face in opposite direction when box moves in gas and on back face in the same direction as

\[v >  > {v_o}\] (box)

Thus, relative velocity on the back face =$\left( {v - {v_o}} \right)$

By a molecule on front face, change in momentum\[ = 2m\left( {v + {v_o}} \right)\]

By a molecule on back side, change in momentum\[ = 2m\left( {v - {v_o}} \right)\]

At $\Delta t$ time, number of molecules striking on the front face $ = \dfrac{1}{2}volume \times molecular\,density\,vo{l^{ - 1}}$

To front face

$ = \dfrac{1}{2}\left[ {A\left( {v + {v_o}} \right)\Delta t} \right]{\rho _m}$

Number of molecules striking to front face

${N_F} = \dfrac{1}{2}\left( {v + {v_o}} \right)A{\rho _m}\Delta t$

As the speed of bloc and molecule striking on backend face 

${N_B} = \dfrac{1}{2}\left( {v - {v_o}} \right)A{\rho _m}\Delta t$

Due to striking the molecule on front face, total change in momentum  

${\rho _F} = 2m\left( {v + {v_o}} \right) \cdot {N_F}$

$ = 2M\left( {v + {v_o}} \right) \times \dfrac{1}{2}\left( {v + {v_o}} \right)A.{\rho _m}\Delta t$

${\rho _F} =  - m{\left( {v + {v_o}} \right)^2}A{\rho _m}\Delta t$ (Backward direction)

Thus, the rate of change of momentum on front face is equal to the force

${F_F} =  - m{\left( {v + {v_o}} \right)^2}A{\rho _m}$ in Backward direction 

Force on back end ${F_B} =  + m{\left( {v - {v_o}} \right)^2}A{\rho _m}$

Net dragging force

$ =  - m{\left( {v + {v_o}} \right)^2}A{\rho _m} + m{\left( {v - {v_o}} \right)^2}A{\rho _m}$

$ =  - mA{\rho _m}\left[ {{{\left( {v + {v_o}} \right)}^2} - {{\left( {v - {v_o}} \right)}^2}} \right]$

$ =  - mA{\rho _m}\left[ {{v^2} + v_o^2 + 2v{v_o} - \left( {{v^2} + v_o^2 - 2v{v_o}} \right)} \right]$

$ =  - mA{\rho _m}4v{v_o}$

Due to gas molecule, magnitude of dragging force $ = 4mv{v_o}A{\rho _m}$

$ = \dfrac{1}{2}m{v^2}$

$ = \dfrac{3}{2}{K_B}T$

$\therefore v = \sqrt {\dfrac{{{K_B}T}}{m}} $ 

$\therefore $ dragging force becomes

$ = 4mA{\rho _m}{v_o}\sqrt {\dfrac{{{K_B}T}}{m}.} $

The kinetic theory is a theory that can be applied to a variety of particles, including atoms and molecules. The characteristics of gasses are frequently studied using kinetic theory. The Brownian motion provides a decent visual representation of particle flow and possible collisions.

Expert Physics teachers at Vedantu deliver NCERT Exemplar Solutions for Class 11 Physics Chapter 13 from the NCERT. In NCERT Exemplar Class 11 Physics, Kinetic Theory is one of the easiest topics. You will learn about ideal gas in this Chapter, which strictly follows gas laws such as Charle's law, Boyle's law, Gay Lussac's law, and others. Graham's law of gas diffusion, kinetic interpretation of temperature, the law of energy equipment, and degrees of freedom are among the Chapter's primary subjects.

Kinetic Theory comprises roughly 5 exercises and a total of 31 problems in Chapter 13. These NCERT Exemplar Class 11 Physics Problems and Solutions for Chapter 13 may aid in exam preparation and revision. While some questions may be difficult to understand at first, with our help, you will be able to complete the exercise. For all exemplar challenges, we always provide step-by-step solutions at Vedantu. To provide you with these answers, our subject matter experts conducted extensive studies on the issues. Read them once and you'll be able to answer all of your questions fast.

NCERT exemplar problem book and Solutions for Class 11 Physics PDF (Download) are available for free on the Vedantu app and website. NCERT Class 11 Physics solutions include both part 1 and part 2 textbook solutions. There are 15 Chapters in the NCERT Solutions for CBSE Class 11 Physics. This website has NCERT exemplar problems and solutions in PDF format for Class 11 Physics. Exemplar Solutions for NCERT Physics Class 11 Only the most recent CBSE curriculum and Physics NCERT Class 11 PDF example questions and solutions are available in Vedantu.

NCERT Physics Exemplar Solutions Class 11 Chapter 13 - Kinetic Theory Important Topics

Theory of Kinetics

According to the kinetic theory of matter, all matter is made up of microscopic elements in random motion with space between them. This demonstrates that matter, regardless of its phase, is made up of discrete, moving constituents.

Matter's Molecular Nature

All things, according to the atomic theory, are made up of minuscule essential units called atoms, which can be described as tiny elements in constant motion that attract or repel each other depending on their inter-particle distance.

Gasses' Behavior

Straight-line motion is unsystematic for gas particles. Gas particles have more kinetic energy than liquid or solid components. Gasses have more kinetic energy than liquids or solids because they exist at higher temperatures.

An Ideal Gas Kinetic Theory

The kinetic theory of gasses assumes that a gas is made up of a vast number of different constituents called molecules. The volume of these molecules has no bearing on the total volume occupied by the gas in an ideal gas.

Law of Energy Equipartition

According to the law of energy equipartition, all degrees of freedom in a dynamical structure in thermal equilibrium share the total energy of the system equally. Each degree of freedom per molecule has a total energy of 21kT, where k is the Boltzmann constant.

Heat Capacity Specification

The quantity of heat energy required to raise the temperature of a material per unit of mass is known as specific heat capacity. It's also an example of a broad property because its value is proportional to the size of the system under examination.

Path of Least Resistance

A gas molecule follows a straight route between every two collisions. The mean free path is the average distance between all of a molecule's routes.

Why should You choose Vedantu's NCERT Physics Exemplar Solutions Class 11 Chapter 13 - Kinetic Theory?

• NCERT Exemplar Problems with Solutions for Class 11 Physics Chapter 13 are available from Vedantu and are of the highest quality, accuracy, and effectiveness

• These NCERT Exemplar solutions might assist you in swiftly comprehending tough topics and then solving questions.

• You can do well in the CBSE Class 12 board exams if you use these problems from the NCERT Exemplar Book.

• Our solutions offer solved problems to assist you in honing your question-solving abilities.