NCERT Exemplar for Class 11 Physics Chapter 15 - Waves (Book Solutions)

MULTIPLE CHOICE QUESTIONS – I

15.1 Water waves produced by a motor boat sailing in water are 

(a) neither longitudinal nor transverse. 

(b) both longitudinal and transverse. 

(c) only longitudinal.

(d) only transverse.

Ans: Option (b) 

Motor boat produces water waves on the surface as well as inside the water. Hence, waves are both transverse and longitudinal.

15.2 Sound waves of wavelength $\lambda $ traveling in a medium with a speed of $\nu {\text{ }}m/\operatorname{s} $ enter into another medium where its speed is $2\nu {\text{ }}m/\operatorname{s} $. Wavelength of sound waves in the second medium is

(a) $\lambda $ 

(b) $\dfrac{\lambda }{2}$ 

(c) $2\lambda $ 

(d) $4\lambda $ 

Ans: Option (c) 

We know that when a wave passes from one medium to another, its velocity and wavelength changes but its frequency remains the same.

We know that, $\nu  = f\lambda $ 

Therefore, we have

$ \Rightarrow f = \dfrac{\nu }{\lambda }....\left( i \right)$

When sound wave enters into another medium, we get

And, $ \Rightarrow f = \dfrac{{2\nu }}{{\lambda '}}.....\left( {ii} \right)$

From $\left( i \right)$ and $\left( {ii} \right)$, we get

$ \Rightarrow \dfrac{\nu }{\lambda } = \dfrac{{2\nu }}{{\lambda '}}$

$ \Rightarrow \dfrac{1}{\lambda } = \dfrac{2}{{\lambda '}}$

$ \Rightarrow \lambda ' = 2\lambda $

15.3 Speed of sound wave in air

(a) is independent of temperature. 

(b) increases with pressure. 

(c) increases with increase in humidity. 

(d) decreases with increase in humidity. 

Ans: Option (c) 

We know that the speed of sound waves (longitudinal wave) in air is given by $\nu  = \sqrt {\dfrac{{\lambda P}}{\rho }} $.

The density of water vapors is less than the air. Thus, on increasing the humidity, density of the medium decreases and this in turn increases the speed of sound in air because $\nu \alpha \dfrac{1}{{\sqrt \rho  }}$.

15.4 Change in temperature of the medium changes 

(a) frequency of sound waves. 

(b) amplitude of sound waves. 

(c) wavelength of sound waves. 

(d) loudness of sound waves. 

Ans: Option (c) 

We know that, ${v_t} = {v_0}\left( {1 + .61t} \right)$ or ${v_t}\alpha \sqrt t $ 

Therefore, on increasing the temperature, speed also increases because frequency doesn’t change during propagation of the wave by formula $V = v\lambda $. 

Hence, velocity $V$ and wavelength $\lambda $ both increase.

15.5 With propagation of longitudinal waves through a medium, the quantity transmitted is 

(a) matter

(b) energy

(c) energy and matter

(d) energy, matter and momentum

Ans: Option (b) 

We know that during propagation of longitudinal waves through a medium, only energy is transmitted from one point to another. Matter doesn’t change its own position as it only vibrates about its mean position.

15.6 Which of the following statements are true for wave motion? 

(a) Mechanical transverse waves can propagate through all mediums. 

(b) Longitudinal waves can propagate through solids only. 

(c) Mechanical transverse waves can propagate through solids only. 

(d) Longitudinal waves can propagate through vacuum. 

Ans: Option (c) 

Transverse waves cannot propagate in gases. Hence, option (a) is incorrect.

Longitudinal waves can propagate through gases. Hence, option (b) is incorrect.

Mechanical transverse waves can propagate through solids and on the surface of liquid also. Hence, option (c) is correct.

Longitudinal waves cannot propagate through vacuum. Hence, option (d) is incorrect.

15.7 A sound wave is passing through an air column in the form of compression and rarefaction. In consecutive compressions and rarefactions, 

(a) density remains constant. 

(b) Boyle’s law is obeyed. 

(c) bulk modulus of air oscillates. 

(d) there is no transfer of heat.

Ans: Option (d) 

We know that the density of medium particles is maximum and minimum at compression and rarefaction point. Therefore option (a) is incorrect.

The temperature of the medium increases because density changes very rapidly. Therefore, option (b) is incorrect.

Option (c) is incorrect because the bulk modulus of air remains constant.

We know that the time of compressions and rarefactions is very small. Thus, heat doesn’t transfer. Hence, option (d) is the correct answer.

15.8 Equation of a plane progressive wave is given by $y = 0.6\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$. On reflection from a denser medium its amplitude becomes $\dfrac{2}{3}$ of the amplitude of the incident wave. The equation of the reflected wave is

(a) $y = 0.6\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$

(b) $y =  - 0.4\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$

(c) $y = 0.4\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$

(d) $y =  - 0.4\sin 2\pi \left( {t - \dfrac{x}{2}} \right)$

Ans: Option (b) 

$y =  - 0.4\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$

After reflection, wave changes by phase $180^\circ $ 

Given equation: $y = 0.6\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$

After reflection, it becomes

$ \Rightarrow {y_r} = \dfrac{2}{3}\sin 2\pi \left( {\pi  + t + \dfrac{x}{2}} \right)$

$ \Rightarrow {y_r} =  - 0.4\sin 2\pi \left( {t + \dfrac{x}{2}} \right)$

15.9 A string of mass $2.5\,kg$ is under a tension of $200\,N$. The length of the stretched string is $20.0\,m$. If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in 

(a) one second 

(b) $0.5$ second 

(c) $2$ seconds 

(d) data given is insufficient. 

Ans: Option (b) 

Mass of string (M) = $2.5kg$

Length of the stretched string ($l$) =  $20m$ 

Mass per unit length = $\dfrac{M}{l}$

$ = \dfrac{{2.5}}{{20}}$ 

$ = 0.125kg/m$ 

We know that $\nu  = \sqrt {\dfrac{T}{\mu }} $. Therefore, we get

$ \Rightarrow \nu  = \sqrt {\dfrac{{200}}{{0.125}}} $

$ \Rightarrow \nu  = \sqrt {1600} $

$ \Rightarrow \nu  = 40m/s$

We know that time = distance/ speed. Therefore, we get

$ \Rightarrow t = \dfrac{{20m}}{{40m/s}}$ 

$ \Rightarrow t = \dfrac{1}{2}\sec $

$ \Rightarrow t = 0.5\sec $

15.10 A train whistling at constant frequency is moving towards a station at a constant speed $V$. The train goes past a stationary observer on the station. The frequency $n'$ of the sound as heard by the observer is plotted as a function of time $t$ (Fig $15.1$ ). Identify the expected curve.

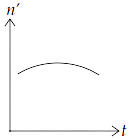
(a)

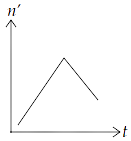
(b)

(c)

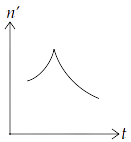
(d)

Ans: option (c)

We know that when observer is at rest and the source of sound is moving towards observer, then observed frequency is given by, $n' = \left( {\dfrac{v}{{v - {v_s}}}} \right){n_o}$, where ${n_o}$ is the original frequency of source of sound, $v$ is speed of sound in medium and ${v_s}$ is speed of source.

$\therefore n' > {n_o}$ 

When source is moving away from the observer,

$ \Rightarrow n' = \left( {\dfrac{v}{{v + {v_s}}}} \right){n_o}$

$\therefore n'' < {n_o}$

Hence, the frequencies in both the cases are the same and $n' > n''$.

MULTIPLE CHOICE QUESTIONS – II MORE THAN ONE OPTION

15.11 A transverse harmonic wave on a string is described by $y\left( {x,t} \right) = 3.0\sin \left( {36t + 0.018x + \dfrac{\pi }{4}} \right)$ 

where $x$ and $y$ are in $cm$ and $t$ is in $s$. The positive direction of $x$ is from left to right. 

(a) The wave is traveling from right to left. 

(b) The speed of the wave is $20m/s$. 

(c) Frequency of the wave is $5.7Hz$. 

(d) The least distance between two successive crests in the wave is $2.5cm$. 

Ans: The correct options are (a), (b) and (c).

The standard equation of a wave propagated from left to right i.e., in $ + ve$ direction is given by $y = a\sin \left( {\omega t - kx + \phi } \right)$ 

Given equation: $y = 3.0\sin \left( {36t + 0.018x + \dfrac{\pi }{4}} \right)$

(a) In the given equation, $x$ is a positive sign. Thus, the given wave travelling from right to left verifies option (a).

(b) From the equation, we have $\omega  = 36$ 

$ \Rightarrow 2\pi f = 36$ 

$ \Rightarrow f = \dfrac{{36}}{{2\pi }}$

$ \Rightarrow f = \dfrac{{18}}{\pi }.....\left( i \right)$

$ \Rightarrow f = \dfrac{{18}}{{3.14}}$

$ \Rightarrow f = 5.7Hz$

From the equation, we have $k = 0.018$ 

$ \Rightarrow \dfrac{{2\pi }}{\lambda } = 0.018$

$ \Rightarrow \dfrac{{2\pi }}{{0.018}} = \lambda $

We know that velocity, $\nu  = f\lambda $. Therefore, we get

$ \Rightarrow \nu  = \dfrac{{18}}{\pi } \times \dfrac{{2\pi }}{{0.018}}$ ($f = \dfrac{{18}}{\pi }.....\left( i \right)$ )

$ \Rightarrow \nu  = \dfrac{{18}}{{0.018}}$

$ \Rightarrow \nu  = 2000cm/s$

$ \Rightarrow \nu  = 20m/s$

This verifies option (b).

(a) From the equation, we have $\omega  = 36$ 

$ \Rightarrow 2\pi f = 36$ 

$ \Rightarrow f = \dfrac{{36}}{{2\pi }}$

$ \Rightarrow f = \dfrac{{18}}{\pi }$

$ \Rightarrow f = \dfrac{{18}}{{3.14}}$

$ \Rightarrow f = 5.7Hz$

This verifies option (c).

(b) Distance between two successive crests is given by, $\lambda  = \dfrac{{2\pi }}{{0.018}}$

$ \Rightarrow \lambda  = \dfrac{\pi }{{0.009}}$

$ \Rightarrow \lambda  = \dfrac{{3.14 \times 1000}}{9}$

$ \Rightarrow \lambda  = \dfrac{{3140}}{9}$

$ \Rightarrow \lambda  = 348.8cm = 3.48m$

Hence, option (d) is incorrect.

15.12 The displacement of a string is given by $y\left( {x,t} \right) = 0.06\sin \left( {\dfrac{{2\pi x}}{3}} \right)\cos \left( {120\pi t} \right)$ 

where $x$ and $y$ are in $m$ and $t$ in $s$. The length of the string is $1.5m$ and its mass is $3.0 \times {10^{ - 2}}kg$. 

(a) It represents a progressive wave of frequency $60Hz$. 

(b) It represents a stationary wave of frequency $60Hz$. 

(c) It is the result of superposition of two waves of wavelength $3m$, frequency $60Hz$ each traveling with a speed of $180m/s$ in opposite direction. 

(d) Amplitude of this wave is constant.

Ans: Options (b) and (c)

We know that the standard equation of stationary wave is $y\left( {x,t} \right) = a\sin \left( {kx} \right)\cos \left( {\omega t} \right)$

Given equation: $y\left( {x,t} \right) = 0.06\sin \left( {\dfrac{{2\pi x}}{3}} \right)\cos \left( {120\pi t} \right)$

(a) The given equation is stationary. Hence option (a) is incorrect.

(b) On comparing standard and given equation, we get $\omega  = 120\pi $ 

$ \Rightarrow 2\pi f = 120\pi $

$ \Rightarrow f = 60Hz$

This verifies option (b).

(a) We know that $k = \dfrac{{2\pi }}{\lambda }$. 

From the given equation, we have $k = \dfrac{{2\pi }}{3}$

$ \Rightarrow \dfrac{{2\pi }}{\lambda } = \dfrac{{2\pi }}{3}$

$ \Rightarrow \lambda  = 3$

Speed, $\nu  = f\lambda $

$ \Rightarrow \nu  = 60 \times 3m/s$

$ \Rightarrow \nu  = 180m/s$

This verifies option (c).

(d) As the waves are stationary, the amplitude of particles varies from $0$ to $0.06$ from nodes to antinodes. Thus, amplitudes throughout the wave are not constant. Hence, the option is incorrect.

15.13 Speed of sound waves in a fluid depends upon 

(a) directly on the density of the medium. 

(b) square of Bulk modulus of the medium. 

(c) inversely on the square root of density. 

(d) directly on the square root of bulk modulus of the medium. 

Ans: Options (c) and (d)

We know the speed of sound waves in the fluid of bulk modulus $k$ and density $\rho $ = $\nu  = \sqrt {\dfrac{k}{\rho }} $.

Therefore, $\nu  = \sqrt k $ (If $\rho $ is constant)

And, $\nu  = \sqrt {\dfrac{1}{\rho }} $ (If $k$ is constant)

Hence, verifies the options (c) and (d).

15.14 During propagation of a plane progressive mechanical wave 

(a) all the particles are vibrating in the same phase. 

(b) the amplitude of all the particles is equal. 

(c) particles of the medium executes S.H.M. 

(d) wave velocity depends upon the nature of the medium. 

Ans: Options (b), (c) and (d)

Each particle between any two successive crests and troughs is in a different mode of vibration or in a different phase. Hence, option (a) is incorrect.

We know that during propagation of mechanical waves each particle displaces from zero to maxima i.e., upto amplitude. Thus, the amplitude of each particle is equal.

Hence, verifies option (b).

For progressive waves, medium particles oscillate about their mean position in which restoring force $F\alpha \left( { - y} \right)$. Therefore, motion of medium particles is simple harmonic motion.

Hence, verifies option (c).

We know that wave velocity is given by $\nu  = \sqrt {\dfrac{k}{\rho }} $.

We can see that $\nu $ depends on $k$ and $\rho $. Also, $k$ and $\rho $ are different for different mediums. Thus, wave velocity depends upon the nature of the medium. Hence, verifies the option (d).

15.15 The transverse displacement of a string (clamped at its both ends) is given by y $y\left( {x,t} \right) = 0.06\sin \left( {\dfrac{{2\pi x}}{3}} \right)\cos \left( {120\pi t} \right)$. All the points on the string between two consecutive nodes vibrate with 

(a) same frequency 

(b) same phase 

(c) same energy

(d) different amplitudes.

Ans: Options (a), (b) and (d)

We know that the standard equation of stationary wave is $y\left( {x,t} \right) = a\sin \left( {kx} \right)\cos \left( {\omega t} \right)$

Given equation: $y\left( {x,t} \right) = 0.06\sin \left( {\dfrac{{2\pi x}}{3}} \right)\cos \left( {120\pi t} \right)$

Thus, the given equation is a stationary wave.

(a) The frequencies of all the particles are the same. Hence, verifies the option (a).

(b) The particles between any two consecutive nodes vibrate either upside or downside having the same phase $120\pi t$ at a time. Hence, verifies the option (b).

(c) We know that amplitudes of different particles are different between two nodes. Also, we know that energy, $E\alpha {A^2}$. Therefore, particles have different energies. Hence, option (c) is incorrect.

(d) Option (c) verifies that option (d) is correct

15.16 A train, standing in a station yard, blows a whistle of frequency $400Hz$ in still air. The wind starts blowing in the direction from the yard to the station with a speed of $10m/s$. Given that the speed of sound in still air is $340m/s$, 

(a) The frequency of sound as heard by an observer standing on the platform is $400Hz$. 

(b) The speed of sound for the observer standing on the platform is $350m/s$. 

(c) the frequency of sound as heard by the observer standing on the platform will increase. 

(d) the frequency of sound as heard by the observer standing on the platform will decrease. 

Ans: Options (a) and (b)

Frequency of whistle is still air, $f = 400Hz$ 

Velocity of wind from source of listener, ${\nu _w} = 10m/s$ 

Speed of sound in still air, ${\nu _s} = 340m/s$ 

Given that, the listener is standing on the platform.

Therefore, speed of sound w.r.t. the listener = ${\nu _s} + {\nu _w} = 340 + 10$ = $350m/s$ 

Hence, verifies option (b).

The distance between listener and source doesn’t change. Thus, the frequency of sound doesn’t change. Therefore, he heard $f = 400Hz$.

Hence, option (c) and (d) are incorrect.

15.17 Which of the following statements are true for a stationary wave? 

(a) Every particle has a fixed amplitude which is different from the amplitude of its nearest particle. 

(b) All the particles cross their mean position at the same time. 

(c) All the particles are oscillating with the same amplitude. 

(d) There is no net transfer of energy across any plane. 

(e) There are some particles which are always at rest.

Ans: Options (a), (b), (d) and (e)

We know that the standard equation of stationary wave is $y\left( {x,t} \right) = a\sin \left( {kx} \right)\cos \left( {\omega t} \right)$

In stationary waves, the particles between the two nodes vibrate with different amplitudes. The amplitude increases from node to antinodes from zero to maximum and then from antinodes to nodes amplitude decreases from maximum to zero. The amplitude of a particle will remain constant, but amplitude will vary with $\lambda $.

$\therefore k = \dfrac{{2\pi }}{\lambda }$. This verifies option (a) and rejects option (c).

The particles present at nodes have amplitude zero. Hence, verifies option (e).

We know that particles at nodes are at rest. Therefore, there is no energy transfer. This verifies option (d).

Particles between the two nodes are in the same phase, it means motion of particles will be either upward or downward. Thus, particles will cross the mean position at the same time. This verifies the option (b).

VERY SHORT ANSWER TYPE QUESTIONS

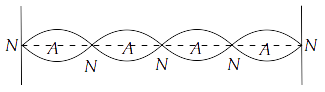
15.18 A sonometer wire is vibrating in resonance with a tuning fork. Keeping the tension applied the same, the length of the wire is doubled. Under what conditions would the tuning fork still resonate with the wire? 

Ans: When a wire of length $L$ vibrates its resonant frequency in $nth$ node after stretching it by a tension $T$ is given by $v = \dfrac{n}{{2L}}\sqrt {\dfrac{T}{m}} $, where $m$ is mass per unit length of stretched wire.

We have two cases:

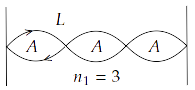
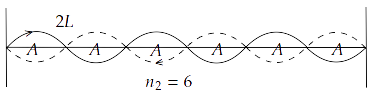
$ \Rightarrow {v_1} = \dfrac{{{n_1}}}{{2{L_1}}}\sqrt {\dfrac{{{T_1}}}{{{m_1}}}} $

$ \Rightarrow {v_2} = \dfrac{{{n_2}}}{{2{L_2}}}\sqrt {\dfrac{{{T_2}}}{{{m_2}}}} $

We are given that,

${T_1} = {T_2} = T$ 

${L_2} = 2{L_1}$ 

The wire is the same. Therefore, ${m_1} = {m_2} = m$

Now, on substituting the values, we get

$ \Rightarrow {v_1} = \dfrac{{{n_1}}}{{2{L_1}}}\sqrt {\dfrac{T}{m}} $

$ \Rightarrow {v_2} = \dfrac{{{n_2}}}{{2 \times 2{L_1}}}\sqrt {\dfrac{T}{m}} $

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\dfrac{{{n_1}}}{{2{L_1}}}\sqrt {\dfrac{T}{m}} }}{{\dfrac{{{n_2}}}{{2 \times 2{L_1}}}\sqrt {\dfrac{T}{m}} }}$

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\dfrac{{{n_1}}}{1}}}{{\dfrac{{{n_2}}}{2}}}$

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{2{n_1}}}{{{n_2}}}$

It is given that the tuning fork is the same. Thus, in both the harmonics ${n_1}$ and ${n_2}$, the frequency of resonance is the same. Therefore,

${v_1} = {v_2} = v$

$ \Rightarrow \dfrac{v}{v} = \dfrac{{2{n_1}}}{{{n_2}}}$

$ \Rightarrow 1 = \dfrac{{2{n_1}}}{{{n_2}}}$

$ \Rightarrow {n_2} = 2{n_1}$

Hence, when length of wire is doubled, the number of harmonics also doubled for the same resonant frequency, tension and mass per unit length.

15.19 An organ pipe of length $L$ open at both ends is found to vibrate in its first harmonic when sounded with a tuning fork of $480Hz$. What should be the length of a pipe closed at one end, so that it also vibrates in its first harmonic with the same tuning fork? 

Ans: Given that, medium, frequency and the number of harmonics in open and closed pipes are the same. Thus, the number of nodes and $\lambda $ in both the cases will also be the same.

In both end open pipe, we have

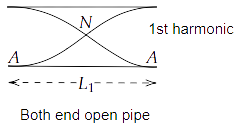
$ \Rightarrow {L_1} = \dfrac{{2 \times {\lambda _1}}}{4}$ 

$ \Rightarrow {L_1} = \dfrac{{{\lambda _1}}}{2}$

$ \Rightarrow {\lambda _1} = 2{L_1}$

We know that $v = \dfrac{c}{\lambda }$. Therefore, we get

$ \Rightarrow {v_1} = \dfrac{c}{{{\lambda _1}}}$

$ \Rightarrow {v_1} = \dfrac{c}{{2{L_1}}}.....\left( i \right)$

In one end open pipe, we have

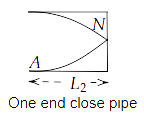
$ \Rightarrow {L_2} = \dfrac{{1 \times {\lambda _2}}}{4}$

$ \Rightarrow {\lambda _2} = 4{L_2}$

And, ${v_2} = \dfrac{c}{{4{L_2}}}.....\left( {ii} \right)$

Given that, the medium and tuning fork in both cases are the same. Therefore, we have ${v_1} = {v_2}$ and ${c_1} = {c_2} = c$.

From the equation $\left( i \right)$ and $\left( {ii} \right)$, we get

$ \Rightarrow \dfrac{c}{{2{L_1}}} = \dfrac{c}{{4{L_2}}}$

$ \Rightarrow {L_1} = 2{L_2}$

$ \Rightarrow {L_2} = \dfrac{{{L_1}}}{2}$

Hence, the length of one end closed pipe will be half of the both end open pipe.

15.20 A tuning fork A, marked $512Hz$, produces $5$ beats per second, where it is sounded with another unmarked tuning fork B. If B is loaded with wax the number of beats is again $5$ per second. What is the frequency of the tuning fork B when not loaded? 

Ans: Given that, ${v_A} = 512$ 

On loading, frequencies of B decreased 

So, in first case ${v_1} = 5$ 

$ \Rightarrow {v_B} = {v_A} \pm 5$ 

When B is loaded, frequency of B becomes,

$ \Rightarrow {v_B} = 512 \pm 5$

We can write it as,

$ \Rightarrow {v_B} = 507$ or ${v_B} = 517$

On load in frequency of B decreased $507$ to lower value of number of beats will increase so ${v_B} \ne 507$

If ${v_B} = 517$ then its frequency decreases $10Hz$ by then the number of beats will also be the same as $512 - 507 = 5$.

Thus, the frequency of the tuning fork B when not loaded is $517Hz$.

15.21 The displacement of an elastic wave is given by the function $y = 3\sin \omega t + 4\cos \omega t $. Where $y$ is in $cm$ and $t$ is in second. Calculate the resultant amplitude. 

Ans: We have, $y = 3\sin \omega t + 4\cos \omega t......\left( i \right)$

Let $3 = a\cos \varphi ......\left( {ii} \right)$ and $4 = a\sin \phi .....\left( {iii} \right)$ 

Thus, equation $\left( i \right)$ becomes  $y = a\cos \varphi \sin \omega t + a\sin \phi \cos \omega t$

$ \Rightarrow y = a\sin \left( {\omega t + \phi } \right)$

From equation $\left( {ii} \right)$ and  $\left( {iii} \right)$, we get

$ \Rightarrow \tan \phi  = \dfrac{4}{3}$

$ \Rightarrow \phi  = {\tan ^{ - 1}}\dfrac{4}{3}$

On squaring and adding the equation $\left( {ii} \right)$ and  $\left( {iii} \right)$, we get

$ \Rightarrow {a^2}{\cos ^2}\varphi  + {a^2}{\sin ^2}\phi  = {3^2} + {4^2}$

$ \Rightarrow {a^2}\left( {{{\cos }^2}\varphi  + {{\sin }^2}\phi } \right) = 9 + 16$

$ \Rightarrow {a^2}\left( 1 \right) = 25$

$ \Rightarrow {a^2} = 25$

$ \Rightarrow a = 5cm$

Hence, the resultant amplitude is $5cm$.

15.22 A sitar wire is replaced by another wire of same length and material but of three times the earlier radius. If the tension in the wire remains the same, by what factor will the frequency change?

Ans: The wire is stretched at both the ends, so frequency of stretched wire is, $v = \dfrac{n}{{2L}}\sqrt {\dfrac{T}{m}} $

As the number of harmonic $n$, length $L$ and tension $T$ are kept the same in both cases.

$\therefore v\alpha \dfrac{1}{{\sqrt m }}$

$\therefore \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\sqrt {{m_2}} }}{{\sqrt {{m_1}} }}.....\left( i \right)$

Mass per unit length $\left( m \right)$  is given by, 

$ = \dfrac{{mass{\text{ }}of{\text{ }}wire}}{{length}}$

$m = \dfrac{{\left( {\pi {r^2}l} \right)\rho }}{l}$

$m = \pi {r^2}\rho $

As the material of the wire is the same. Therefore, we get

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \sqrt {\dfrac{{\pi r_2^2\rho }}{{\pi r_1^2\rho }}} $

Given that, the sitar wire is replaced by another wire of three times the earlier radius.

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \sqrt {\dfrac{{{{\left( {3r} \right)}^2}}}{{{r^2}}}} $

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{3r}}{r}$

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{3}{1}$

$\therefore {v_2} = \dfrac{1}{3}{v_1}$

Thus, the frequency of sitar is reduced by  $\dfrac{1}{2}$ of previous value.

15.23 At what temperatures (in $^\circ C$ ) will the speed of sound in air be $3$ times its value at $0^\circ C$ ?

Ans: We know that $\nu \alpha \sqrt T $ 

$ \Rightarrow \dfrac{{{\nu _T}}}{{{\nu _0}}} = \sqrt {\dfrac{T}{{{T_0}}}} $ 

Given that, ${\nu _T} = 3{\nu _0}$ 

$\therefore \dfrac{{3{\nu _0}}}{{{\nu _0}}} = \sqrt {\dfrac{T}{{273 + 0}}} $ 

$ \Rightarrow \sqrt T  = 3\sqrt {273} $

$ \Rightarrow T = 9 \times 273$

$ \Rightarrow T = 2457K$

$ \Rightarrow T = 2457 - 273$

$ \Rightarrow T = 2184{}^\circ C$

15.24 When two waves of almost equal frequencies ${n_1}$ and ${n_2}$ reach at a point simultaneously, what is the time interval between successive maxima? 

Ans: Given that, the two frequencies are almost equal, ${n_1} = {n_2}$ 

For formation of the beats, the frequencies must be ${n_2} > {n_1}$ 

Number of frequency per second in maxima = $n$ = ${n_2} - {n_1}$

Thus, time period of beats or maxima = $\dfrac{1}{n}$ = $\dfrac{1}{{{n_2} - {n_1}}}\sec $ 

SHORT ANSWER TYPE QUESTIONS

15.25 A steel wire has a length of $12m$ and a mass of $2.10kg$. What will be the speed of a transverse wave on this wire when a tension of $2.06 \times {10^4}N$ is applied? 

Ans: We have, length of steel wire, $l$ = $12m$ 

Total mass of steel wire, $M$ = $2.10kg$ 

Tension, $T$ = $2.06 \times {10^4}N$

We know that  $m = \dfrac{M}{l}$. Therefore we get

$ \Rightarrow m = \dfrac{{2.10}}{{12}}$

We know that $v = \sqrt {\dfrac{T}{m}} $. Therefore, we get

$ \Rightarrow v = \sqrt {\dfrac{{2.06 \times {{10}^4} \times 12}}{{2.10}}} $

$ \Rightarrow v = \sqrt {\dfrac{{1236 \times {{10}^4}}}{{105}}} $

$ \Rightarrow v = \sqrt {11.77}  \times {10^2}m/s$

$ \Rightarrow v = 3.43 \times {10^2}m/s$

$ \Rightarrow v = 343.0m/s$

15.26 A pipe $20cm$ long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a source of $1237.5Hz$ ?(sound velocity in air = $330m{s^{ - 1}}$ ) 

Ans: We have, length of the pipe, $l$ = $20cm$ = $0.2m$ 

And, $v = 1237.5Hz$

Sound velocity in air, $\nu $ = $330m{s^{ - 1}}$

$l = \dfrac{\lambda }{4}$ or $\lambda  = 4l$ 

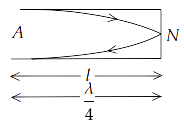
For fundamental frequency, ${v_1} = \dfrac{\nu }{\lambda } = \dfrac{\nu }{{4l}}$. Therefore, we get

$ \Rightarrow {v_1} = \dfrac{{330}}{{4 \times 20 \times {{10}^{ - 2}}}}$

$ \Rightarrow {v_1} = 412.5Hz$

$v\left( {given} \right) = 1237.5Hz$ 

$ \Rightarrow \dfrac{{v\left( g \right)}}{{{v_1}}} = \dfrac{{1237.5Hz}}{{412.5Hz}}$ 

$ \Rightarrow \dfrac{{v\left( g \right)}}{{{v_1}}} = \dfrac{3}{1}$

Hence, the frequencies in $Ist,IInd,IIIrd,....$ harmonic are in the ratio $1:2:3:4...$ in one end open pipe. 

15.27 A train standing at the outer signal of a railway station blows a whistle of frequency $400Hz$ still air. The train begins to move with a speed of $10m{s^{ - 1}}$ towards the platform. What is the frequency of the sound for an observer standing on the platform? (sound velocity in air = $330m{s^{ - 1}}$ ) 

Ans: Frequency of train standing at the outer signal, ${v_o} = 400Hz$ 

Speed of train moving towards platform, ${\nu _s}$  = $10m{s^{ - 1}}$

Velocity of sound in air, ${\nu _a} = 330m{s^{ - 1}}$ 

Apparent frequency of the sound for an observer standing on platform,

$ \Rightarrow v' = \dfrac{{{\nu _a}}}{{\left( {{\nu _a} - {\nu _s}} \right)}}{v_o}$ 

$ \Rightarrow v' = \dfrac{{330 \times 400}}{{\left( {330 - 10} \right)}}Hz$

$ \Rightarrow v' = \dfrac{{330 \times 400}}{{320}}Hz$

$ \Rightarrow v' = \dfrac{{825}}{2}Hz$

$ \Rightarrow v' = 412.5Hz$

15.28 The wave pattern on a stretched string is shown in Fig. $15.2$. Interpret what kind of wave this is and find its wavelength.

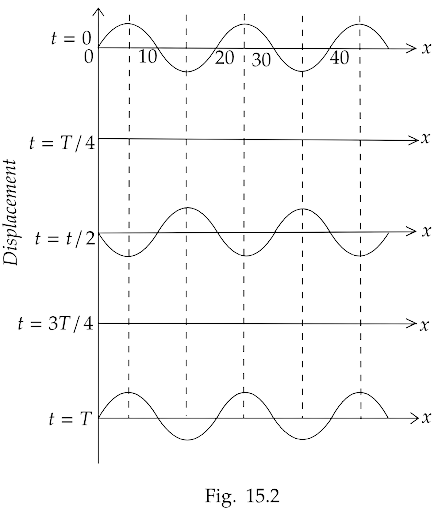
Ans: All particles are at rest at $t = \dfrac{T}{4}$ and $t = \dfrac{{3T}}{4}$, which is in stationary wave when the particle crosses its mean position.

Thus, the graph shows a stationary wave. The wave at $x = 10,20,30,40cm$ there are nodes and distance between successive nodes is $\dfrac{\lambda }{2}$.

$\therefore \dfrac{\lambda }{2} = \left( {30 - 20} \right)$ 

$ \Rightarrow \lambda  = 20cm$

15.29 The pattern of standing waves formed on a stretched string at two instants of time are shown in Fig. $15.3$. The velocity of two waves superimposing to form stationary waves is $360m{s^{ - 1}}$ and their frequencies are $256Hz$. 

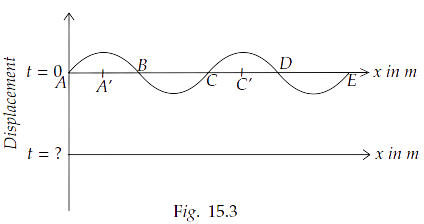
(a) Calculate the time at which the second curve is plotted. 

Ans: Given, Velocity $\nu  = 360m{s^{ - 1}}$ 

Frequency of wave, $f$ = $256Hz$

$\therefore T = \dfrac{1}{f}$ 

$ \Rightarrow T = \dfrac{1}{{256}}\sec $

$ \Rightarrow T = 0.00390$

$ \Rightarrow T = 3.9 \times {10^{ - 3}}\sec $

In stationary wave, when particle’s mean position changes after $\dfrac{T}{4}$, the time is calculated as

$t=\dfrac{T}{4}= \dfrac{3.9 \times {10^{ - 3}}}{4}= 9.8 \times 10^{-4}\,sec$

(b) Mark nodes and antinodes on the curve.

Ans: Point doesn’t vibrate i.e., their displacement is zero always. So nodes are at A,B,C,D and E. The points A’ and C’ are at maximum displacement. So, the antinodes are A’ and C’.

(c) Calculate the distance between A′ and C′. 

Ans: Distance between A’ and C’ is given by, $\lambda  = \dfrac{\nu }{f}$ 

$ \Rightarrow \lambda  = \dfrac{{360}}{{256}}$

$ \Rightarrow \lambda  = 1.41m$

15.30 A tuning fork vibrating with a frequency of $512Hz$ is kept close to the open end of a tube filled with water (Fig. $15.4$ ). The water level in the tube is gradually lowered. When the water level is $17cm$ below the open end, maximum intensity of sound is heard. If the room temperature is $20{}^\circ C$, calculate 

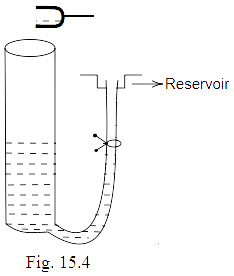
(a) speed of sound in air at room temperature 

Ans: Pipe partially filled with water behaves like a one end open organ pipe. In the 1st harmonic, one antinode and one node at water level are formed, so the first harmonic or at maximum intensity is heard at $L = 17cm$. So,

$L = \dfrac{\lambda }{4}$ 

$ \Rightarrow \lambda  = 4L$

$ \Rightarrow \lambda  = 4 \times 17$

$ \Rightarrow \lambda  = 68cm$

$ \Rightarrow \lambda  = 0.68m$

Frequency of tuning fork, $f$ = $512Hz$ 

Velocity of sound in air, $\nu  = \lambda f$. Therefore, we get

$ \Rightarrow \nu  = 0.68 \times 512m/s$ 

$ \Rightarrow \nu  = 348.16m/s$

Thus, velocity of sound in air at room temperature $20{}^\circ C$ is $348.16m/s$

(b) speed of sound in air at $0{}^\circ C$ 

Ans: We know that, $\nu \alpha \sqrt T $ 

$ \Rightarrow \dfrac{{{\nu _0}}}{{{\nu _T}}} = \sqrt {\dfrac{{{T_0}}}{T}} $ 

${T_0} = 273K$ 

${\nu _T} = {\nu _{20}} = 348.16$ 

$T = 20 + 273 = 293K$ 

$ \Rightarrow {\nu _0} = {\nu _T}\sqrt {\dfrac{{{T_0}}}{{{T_T}}}} $

$ \Rightarrow {\nu _0} = 348.16\sqrt {\dfrac{{273}}{{293}}} $

$ \Rightarrow {\nu _0} = 348.16\sqrt {0.9317} $

$ \Rightarrow {\nu _0} = 348.16 \times 0.96526$

$ \Rightarrow {\nu _0} = 336m/s$

(c) if the water in the tube is replaced with mercury, will there be any difference in your observations?

Ans: The sound is reflected into the air column by water and mercury to form a stationary wave. Mercury is denser than water, this reflection is more in mercury than water. So, the intensity of sound heard will be larger but reading doesn’t change as the medium in tube (air) and tuning fork are the same.

15.31 Show that when a string fixed at its two ends vibrates in $1$ loop, $2$ loops, $3$ loops and $4$ loops, the frequencies are in the ratio $1:2:3:4$.

Ans: Let the number of loops in the string be $n$ 

Length of each loop = $\dfrac{\lambda }{2}$ 

$\therefore L = \dfrac{{n\lambda }}{2}$ or $\lambda  = \dfrac{{2L}}{n}$

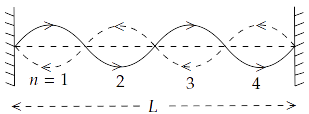
We know that velocity, $\upsilon  = \lambda v$. Therefore, we get

$ \Rightarrow \dfrac{\upsilon }{v} = \lambda $

$ \Rightarrow \dfrac{\upsilon }{v} = \dfrac{{2L}}{n}$

So, $v = \dfrac{n}{{2L}}.\upsilon $

We know that $\upsilon  = \sqrt {\dfrac{T}{m}} $  for a stretch string.

$ \Rightarrow v = \dfrac{n}{{2L}}\sqrt {\dfrac{T}{m}} $

For $n = 1$, ${v_1} = \dfrac{1}{{2L}}\sqrt {\dfrac{T}{m}}  = {v_0}$ 

For $n = 2$, ${v_2} = \dfrac{2}{{2L}}\sqrt {\dfrac{T}{m}}  = 2{v_0}$ 

For $n = 3$, ${v_3} = \dfrac{3}{{2L}}\sqrt {\dfrac{T}{m}}  = 3{v_0}$ 

For $n = 4$, ${v_4} = \dfrac{4}{{2L}}\sqrt {\dfrac{T}{m}}  = 4{v_0}$

Therefore, ${v_1}:{v_2}:{v_3}:{v_4} = 1:2:3:4$ 

LONG ANSWER TYPE QUESTIONS

15.32 The earth has a radius of $6400km$. The inner core of $1000km$ radius is solid. Outside it, there is a region from $1000km$ to a radius of $3500km$ which is in molten state. Then again from $3500km$ to $6400km$ the earth is solid. Only longitudinal $\left( P \right)$ waves can travel inside a liquid. Assume that the $P$ wave has a speed of $8km{\text{ }}{s^{ - 1}}$ in solid parts and of $5km{\text{ }}{s^{ - 1}}$ in liquid parts of the earth. An earthquake occurs at some place close to the surface of the earth. Calculate the time after which it will be recorded in a seismometer at a diametrically opposite point on the earth if the wave travels along diameter?

Ans: We have,

${r_1} = 1000km$ 

${r_2} = 3500km$

${r_3} = 6400km$

${d_1} = 1000km$

${d_2} = 3500 - 1000 = 2500km$

${d_3} = 6400 - 3500 = 2900km$

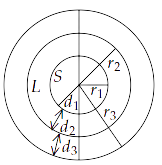
Solid distance diametrically = $2\left( {{d_1} + {d_3}} \right)$ 

$ = 2\left( {1000 + 2900} \right)$

$ = 2 \times 3900km$

Thus, time taken by wave produced by earthquake in solid part = $\dfrac{{3900 \times 2}}{8}\sec $ 

Liquid part along diametrically = $2{d_2}$ = $2 \times 2500$ 

Thus, time taken by seismic wave in liquid part = $\dfrac{{2500 \times 2}}{5}\sec $

Total time = $\dfrac{{3900 \times 2}}{8} + \dfrac{{2500 \times 2}}{5}$

$ = 2\left( {\dfrac{{3900}}{8} + \dfrac{{2500}}{5}} \right)$

$ = 2\left( {487.5 + 500} \right)$

$ = 2 \times 987.5$

$ = 1975\sec $

$ = 32\min 55\sec $ 

Therefore, the required answer is $32\min 55\sec $.

15.33 If $c$ is r.m.s. the speed of molecules in a gas and $\nu $ is the speed of sound waves in the gas, showing that $\dfrac{c}{\nu }$ is constant and independent of temperature for all diatomic gases.

Ans: We know that for molecules, $c = \sqrt {\dfrac{{3P}}{\rho }} $.

We know that $\dfrac{p}{\rho } = \dfrac{{PT}}{M}$. Therefore, we get

$ \Rightarrow \dfrac{P}{\rho } = \dfrac{{RT/V}}{{M/V}}$

$ \Rightarrow \dfrac{P}{\rho } = \dfrac{{RT}}{M}$

Thus, we can write the equation for the molecules as,

$ \Rightarrow c = \sqrt {\dfrac{{3RT}}{M}} $

Where $M$ is the molar mass of gas.

For sound waves, we have

$ \Rightarrow \nu  = \sqrt {\dfrac{{\gamma P}}{\rho }} $

We know that $PV = nRT$. For $n = 1$, we have

$ \Rightarrow P = \dfrac{{RT}}{V}$

Thus, we get $ \Rightarrow \nu  = \sqrt {\dfrac{{\gamma RT}}{M}} $

$ \Rightarrow \dfrac{c}{\nu } = \dfrac{{\sqrt {\dfrac{{3RT}}{M}} }}{{\sqrt {\dfrac{{\gamma RT}}{M}} }}$ 

$ \Rightarrow \dfrac{c}{\nu } = \sqrt {\dfrac{3}{\gamma }} $

We know that $\gamma  = \dfrac{{{C_P}}}{{{C_\nu }}} = \dfrac{7}{5}$ is adiabatic constant for diatomic gas. Therefore, we get

$ \Rightarrow \dfrac{c}{\nu } = \sqrt {\dfrac{3}{{\dfrac{7}{5}}}} $

$ \Rightarrow \dfrac{c}{\nu } = \sqrt {\dfrac{{3 \times 5}}{7}} $

$ \Rightarrow \dfrac{c}{\nu } = \sqrt {\dfrac{{15}}{7}} $ = constant.

15.34 Given below are some functions of $x$ and $t$ to represent the displacement of an elastic wave. 

(i) $y = 5\cos \left( {4x} \right)\sin \left( {20t} \right)$ 

(ii) $y = 4\sin \left( {5x - \dfrac{t}{2}} \right) + 3\cos \left( {5x - \dfrac{t}{2}} \right)$ 

(iii) $y = 10\cos \left[ {\left( {252 - 250} \right)\pi t} \right]\cos \left[ {\left( {252 + 250} \right)\pi t} \right]$

(iv) $y = 100\cos \left( {100\pi t + 0.5x} \right)$

State which of these represent 

(a) a traveling wave along $ - x$ direction 

Given reasons for your answers. 

Ans: A traveling wave along $\left( { - x} \right)$ direction must have $ + kx$ i.e., in (iv) $y = 100\cos \left( {100\pi t + 0.5x} \right)$

(b) a stationary wave

Ans: When a stationary wave is there, we have (i) $y = 5\cos \left( {4x} \right)\sin \left( {20t} \right)$

(c) beats

Ans: Beats involve $\left( {{v_1} + {v_2}} \right)$ and $\left( {{v_1} - {v_2}} \right)$. So, beats can be represented by (iii) $y = 10\cos \left[ {\left( {252 - 250} \right)\pi t} \right]\cos \left[ {\left( {252 + 250} \right)\pi t} \right]$

(d) a traveling wave along $ + x$ direction. 

Ans: $y = 4\sin \left( {5x - \dfrac{t}{2}} \right) + 3\cos \left( {5x - \dfrac{t}{2}} \right).....\left( i \right)$

Let $4 = a\cos \phi ....\left( {ii} \right)$ 

And, $3 = a\sin \phi .....\left( {iii} \right)$ 

On squaring and adding equation $\left( {ii} \right)$ and $\left( {iii} \right)$, we get

$ \Rightarrow {a^2}{\sin ^2}\phi  + {a^2}{\cos ^2}\phi  = {3^2} + {4^2}$

$ \Rightarrow {a^2}\left( {{{\sin }^2}\phi  + {{\cos }^2}\phi } \right) = 9 + 16$

$ \Rightarrow {a^2} = 25$

$ \Rightarrow a = 25$

On substituting $\left( {ii} \right)$ and $\left( {iii} \right)$ in equation  $\left( i \right)$, we get

$ \Rightarrow y = a\cos \phi \sin \left( {5x - \dfrac{t}{2}} \right) + a\sin \phi \cos \left( {5x - \dfrac{t}{2}} \right)$

$ \Rightarrow y = a\sin \left( {5x - \dfrac{t}{2} + \phi } \right)$

$ \Rightarrow y = 5\sin \left( {5x - \dfrac{t}{2} + \phi } \right)$

We can see in the above written equation that the signs of $5x$ and  $\dfrac{1}{2}t$  are opposite. Hence, the wave travels in $ + x$. direction. Therefore, the correct answer is (ii).

15.35 In the given progressive wave $y = 5\sin \left( {100\pi t - 0.4\pi x} \right)$ where $y$ and $x$ are in $m$, $t$ is in $s$. What is the 

(a) amplitude 

Ans: Wave is traveling in $ + x$ direction because $\omega t$ and $kx$ have opposite signs.

Standard equation is given by, $y = a\sin \left( {\omega t - kx + \phi } \right)$

We have, $y = 5\sin \left( {100\pi t - 0.4\pi x} \right)$

Therefore, on comparing we get $a = 5m$, $\omega  = 100\pi $, $k = 0.4\pi $.

(a) Amplitude, $a = 5m$ 

(b) Wavelength $\lambda $ 

Ans: We know that, $k = \dfrac{{2\pi }}{\lambda }$. Therefore, we get

$ \Rightarrow \lambda  = \dfrac{{2\pi }}{k}$

We have, $k = 0.4\pi $

$ \Rightarrow \lambda  = \dfrac{{2\pi }}{{0.4\pi }}$

$ \Rightarrow \lambda  = 5m$

(c) Frequency $v$ 

Ans: We know that, $\omega  = 2\pi v$. Therefore, we get

$ \Rightarrow v = \dfrac{\omega }{{2\pi }}$

We have, $\omega  = 100\pi $

$ \Rightarrow v = \dfrac{{100\pi }}{{2\pi }}$

$ \Rightarrow v = 50Hz$

(d) Wave velocity $\upsilon $ 

Ans: We know that, $\upsilon  = \lambda v$. Therefore, we get

$ \Rightarrow \upsilon  = 5 \times 50$ 

$ \Rightarrow \upsilon  = 250m/s$

(e) particle velocity amplitude. 

Ans: Particle velocity at a distance $x$ from source in the direction of amplitude,

$ \Rightarrow y = 5\sin \left( {100\pi t - 0.4\pi x} \right)$ 

$ \Rightarrow \dfrac{{dy}}{{dt}} = 5 \times 100\pi \cos \left( {100\pi t - 0.4\pi x} \right)$

For maximum velocity, particle is at its mean position

$ \Rightarrow \cos \left( {100\pi t - 0.4\pi x} \right) = 1$

$ \Rightarrow 100\pi t - 0.4\pi x = 0$

$\therefore {\left( {\dfrac{{dy}}{{dt}}} \right)_{\max }} = 5 \times 100\pi  \times 1$

Thus, ${\nu _{\max }}$ of medium particle = $500\pi m/s$.

15.36 For the harmonic traveling wave $y = 2\cos 2\pi \left( {10t - 0.0080x + 3.5} \right)$ where $x$ and $y$ are in $cm$ and $t$ is second. What is the phase difference between the oscillatory motion at two points separated by a distance of 

(a) $4m$  

Ans: We have, $y = 2\cos 2\pi \left( {10t - 0.0080x + 3.5} \right)$

$ \Rightarrow y = 2\cos \left( {20\pi t - 0.016\pi x + 3.5\pi } \right)$

Wave is propagated in the $ + x$ direction because $\omega t$ and  $kx$ have opposite signs.

We know that the standard equation is, $y = a\cos \left( {\omega t - kx + \phi } \right)$.

Therefore, we get $a = 2$, $\omega  = 20\pi $, $k = 0.016\pi $ and  $\phi  = 7\pi $.

We know that phase difference $\vartriangle \phi  = \dfrac{{2\pi }}{\lambda } \times p$, where $\dfrac{{2\pi }}{\lambda } = k$. 

So, we get $\vartriangle \phi  = k \times p$. 

Given that, path difference $p = 4m$.

$ \Rightarrow p = 400cm$ 

$ \Rightarrow \vartriangle \phi  = k \times 400$

$ \Rightarrow \vartriangle \phi  = 0.016\pi  \times 400$

$ \Rightarrow \vartriangle \phi  = 6.4\pi {\text{ }}radian$

Hence, phase difference = $6.4\pi {\text{ }}radian$.

(b) $0.5m$ 

Ans: Given that, path difference $p = 0.5m$.

$ \Rightarrow p = 50cm$ 

$ \Rightarrow \vartriangle \phi  = k \times 50$

$ \Rightarrow \vartriangle \phi  = 0.016\pi  \times 50$

$ \Rightarrow \vartriangle \phi  = 0.8\pi {\text{ }}radian$

Hence, phase difference = $0.8\pi {\text{ }}radian$.

(c) $\dfrac{\lambda }{2}$ 

Ans: Given that, path difference p $= \dfrac{\lambda }{2}$.

We know that $\vartriangle \phi  = \dfrac{{2\pi }}{\lambda } \times p$. Therefore, we get

$ \Rightarrow \vartriangle \phi  = \dfrac{{2\pi }}{\lambda } \times \dfrac{\lambda }{2}$ 

$ \Rightarrow \vartriangle \phi  = \pi {\text{ }}radian$

Hence, phase difference = $\pi {\text{ }}radian$.

(d) $\dfrac{{3\lambda }}{4}$ (at a given instant of time)

Ans: Given that, path difference $p = \dfrac{{3\lambda }}{4}$.

We know that $\vartriangle \phi  = \dfrac{{2\pi }}{\lambda } \times p$.Therefore, we get

$ \Rightarrow \vartriangle \phi  = \dfrac{{2\pi }}{\lambda } \times \dfrac{{3\lambda }}{4}$ 

$ \Rightarrow \vartriangle \phi  = \dfrac{{3\pi }}{2}{\text{ }}radian$

Hence, phase difference =$\pi {\text{ }}radian$.

(e) What is the phase difference between the oscillation of a particle located at $x = 100cm$, at $t = T{\text{ }}s$ and $t = 5s$ ?

Ans: We know that $T = \dfrac{{2\pi }}{\omega }$.On substituting the value of $\omega  = 20\pi $, we get

$ \Rightarrow T = \dfrac{{2\pi }}{{20\pi }}$

$ \Rightarrow T = \dfrac{1}{{10}}\sec $

We have,

$x = 100cm$ 

$t = T$ 

At $x = 100cm$, $t = T$ 

$ \Rightarrow {\phi _1} = 20\pi T - 0.016\pi \left( {100} \right) + 7\pi $ 

$ \Rightarrow {\phi _1} = 20\pi \dfrac{1}{{10}} - 1.6\pi  + 7\pi $

$ \Rightarrow {\phi _1} = 2\pi  - 1.6\pi  + 7\pi $

$ \Rightarrow {\phi _1} = 7.4\pi $

At $x = 100cm$, $t = 5s$ 

$ \Rightarrow {\phi _2} = 20\pi \left( 5 \right) - 0.016\pi \left( {100} \right) + 7\pi $ 

$ \Rightarrow {\phi _2} = 100\pi  - 1.6\pi  + 7\pi $

$ \Rightarrow {\phi _2} = 105.4\pi $

Therefore, phase difference = ${\phi _2} - {\phi _1}$ 

$ \Rightarrow 105.4\pi  - 7.4\pi  = 98\pi {\text{ }}radian$

NCERT exemplar Class 11 Physics Chapter 15 waves is available in PDF format for students to browse and download. This solution solves the problems in the NCERT Exemplar book, assisting in the knowledge of the material from an exam perspective.

NCERT exemplar Class 11 Physics Chapter 15 PDF contains waves Class 11 essential questions, waves problems and solutions, MCQ'S, short answer questions, worksheets and exercises that assist you in taking waves to Class 11 NCERT notes and ultimately save you time when revising the themes.

A disturbance that transfers energy over time and space is referred to as a wave. Mechanical and electromagnetic waves are two forms of waves. When sound waves collide with their neighbors, they travel through the air molecules.

Waves are formed by difficulties that move across a given medium due to the frequent periodic motion of the elements around their mean position, as explained in NCERT Exemplar Solutions for Class 11 Physics Chapter 15. The features of waves, basic wave terminology, varieties of waves, wave reflection, traveling wave speed, Doppler Effect, displacement relation in a progressive wave, and beats will all be covered.

All of the topics in the NCERT Exemplar Class 11 Physics Solutions are covered in this book. Examples and pictorial representations are used to teach Physics Chapter 15. This aids in a better understanding of the notion of waves. There are five exercises in Chapter 15 with a total of 36 sample problems. All of the questions are based on the most recent NCERT pattern.

Expert Physics lecturers with a lot of experience have developed the Exemplar solutions. We've also organized the problems in NCERT Exemplar Chapter 15 by topic so that you can work through them one at a time and build your self-confidence as you go. You can access the solutions from any location and at any time.

Forms Of Waves

1. Microwaves

2. Infrared radiation

3. Gamma rays

4. X-rays

5. Radio waves

6. Ultraviolet radiation

Topics Covered In Chapter Of  In Class 11 Physics Waves

1. Longitudinal and transverse waves

2. In a progressive wave, the displacement relation

3. The speed at which a wave travels.

4. The principle of wave superposition

5. Waves are reflected.

6. It outperforms the Doppler Effect.

NCERT Physics Exemplar Solutions Class 11 Chapter 15 – Waves: Exercise-By-Exercise Discussion

(Exercise 15.1 – Multiple Choice Questions)

This is the first exercise in the Chapter, and it consists of ten multiple-choice questions based on the Chapter's key subjects.

Multiple Choice Questions II (Exercise 15.2)

The second exercise in the NCERT Exemplar Class 11 Solutions for Chapter 15 comprises seven multiple-choice questions.

Exercise 15.3 - Questions with Very Short Answers

This Chapter's exercise comprises roughly 7 questions, all of which are relatively short answer type questions based on wave features and basic terminologies.

Exercise 15.4 –Questions with a Short Answer

Chapter 15 'Waves' practise contains seven short answer questions. Practicing these questions will help you understand what you're learning.

Long Answer Type Questions (Exercise 15.5)

The long answer type questions in Exercise 15.5 of NCERT Exemplar Solutions for Class 11 Physics Chapter 15 are based on the topics types of waves, a reflection of waves, speed of a traveling wave, Doppler Effect, displacement relation in a progressive wave, and beats.

Why Should You Choose Vedantu’s NCERT Physics Exemplar Solutions Class 11 Chapter 15 - Waves?

• Because the solutions to the NCERT Exemplar questions are correct and to the point, you will have an advantage over the other students.

• These solutions cover all of the essential ideas that will enable you to confidently answer all of the problems on the CBSE examinations.

• The NCERT Exemplar Class 11 Physics Solutions for Chapter 15 will make scoring marks much easier for you.

• The most important aspect is that the solutions we develop are completely free for you.

• All NCERT Exemplar solutions are written in compliance with CBSE's most recent guidelines.