NCERT Exemplar for Class 11 Physics Chapter 6 - Work, Energy and Power (Book Solutions)

6.1 An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is because,

(a) the two magnetic forces are equal and opposite, so they produce no net effect.

(b) the magnetic forces do not work on each particle.

(c) the magnetic forces do equal and opposite (but non-zero) work on each particle.

(d) the magenetic forces are necessarily negligible.

Ans: (b) obtion is correct.

The Work Energy Theorem states that net work done Equals final kinetic energy - initial kinetic energy of the item. 

The following equation demonstrates the relationship between work and kinetic energy:

$\Sigma {\text{W}} = {{\text{K}}_2} - {{\text{K}}_1}$v

As the electron and proton move under the influence of mutual interactions, the magnetic forces will be perpendicular to their motion, acting as a centripetal force for the particle. 

As a result of performing the uniform circular motion in this manner, the particle's speed remains constant. 

As a result, the particle's kinetic energy remains unchanged. 

As a result, these forces perform no work.

$\overrightarrow {{F_m}}  = q(\vec v \times \vec B) \cdot {F_m}$

(magnetic force) will be perpendicular to both B and v, where B represents the external magnetic field and v represents particle velocity. 

That is why the magnetic pull of one particle on another is ignored.

6.2 A proton is kept at rest. A positively charged particle is released from rest at a distance d in its field. Consider two experiments; one in which the charged particle is also a proton and in another, a positron. In the same time t, the work done on the two moving charged particles is 

(a) the same force law is involved in the two experiments.

(b) less for the case of a positron, as the positron moves away more rapidly and the force on it weakens.

(c) more for the case of a positron, as the positron moves away a larger distance.

(d) same as the work done by charged particles on the stationary proton.

Ans: (c) obtion is correct.

Because their charges are equivalent, the force between two protons is equal to the force between a proton and a positron. 

Because the mass of the positron is substantially lower than that of the proton, it travels a far greater distance (\[(1/1840\]times) than the proton.

Their motion will remain constant. 

As a result, the velocity of a lighter particle is greater than that of a heavier particle. 

As a result, the positron travels a greater distance.

As force x distance = work done 

Because the forces are the same in the case of a proton and a positron, but the distance traversed by the positron is more, the work done will be greater.

6.3 A man squatting on the ground gets straight up and stands. The force of reaction of ground on the man during the process is

(a) constant and equal to mg in magnitude.

(b) constant and greater than mg in magnitude.

(c) variable but always greater than mg.

(d) at first greater than mg, and later becomes equal to mg.

Ans: (d) obtion is correct.

While crouching on the ground, he straightens up and stands. 

The guy is then tilted slightly, and he exerts a varied force on the ground to balance his weight, thus he must also balance frictional force in this situation, in addition to his weight.
N\[ = \] Normal reaction force \[ = \] friction $ + mg =  > N > mg$

Once the man stands up straight, that variable force will be released. 

Normal reaction force $ = {\text{mg}}$

6.4 A bicyclist comes to a skidding stop in $10{\text{m}}$. During this process, the force on the bicycle due to the road is $200{\text{N}}$ and is directly opposed to the motion. The work done by the cycle on the road is

(a) $ + 2000{\text{J}}$

(b) $ - 200{\text{J}}$

(c) $0$

(d) $ - 20,000{\text{J}}$

Ans: (c) obtion is correct.

Because friction exists in this scenario, mechanical energy is not conserved. 

As a result, energy will be wasted owing to frictional dissipation. 

The frictional force on the cycle does work here, and it is equivalent to $200 \times 10 =  - 2000{\text{J}}$

Because the road is immobile, the work done by the cycle on the road is nil.

We should be aware that the energy of the biker is lost during motion, but it is lost in the form of heat due to friction.

6.5 A body is falling freely under the action of gravity alone in vacuum. Which of the following quantities remain constant during the fall?

(a) Kinetic energy.

(b) Potential energy.

(c) Total mechanical energy.

(d) Total linear momentum.

Ans: (c) obtion is correct.

On A, Mechanical Energy, ${\text{ }}{E_A} = KE + PE$

${E_A} = \frac{1}{2}m{v^2} + mgH$

As velocity is going to be zero at A, 

$K.E. = 0$ 

\[{E_A} = m{\text{ }}g{\text{ }}H\]

Velocity at point B, ${v_B} = \sqrt {2gh}$

So energy at point B, ${E_B} = {\text{KE}} + {\text{PE}}$

${E_B} = \frac{1}{2}m(2gh) + mg(H - h)$

${E_B} = mgh + mgH - mgh$

${E_B} = mgH$ 

Velocity at point C, ${v_c} = \sqrt {2gh}$

Energy at point C, ${E_C} = {\text{KE}} + {\text{PE}}$

${E_C} = \frac{1}{2}m(2gH) + mg(0)$

${E_C} = mgH$ 

6.6 During inelastic collision between two bodies, which of the following quantities always remain conserved?

(a) Total kinetic energy.

(b) Total mechanical energy.

(c) Total linear momentum.

(d) Speed of each body.

Ans: (c) obtion is correct.

If the kinetic energy after a collision is more than the kinetic energy before the contact, the collision is said to be inelastic.

\[{\text{0 < e < 1}}\]

When we regard the two bodies as a system, the total external force acting on the system is zero. As a result, the system's entire linear momentum is preserved.

In this case, kinetic energy manifests itself in different ways, such as heat and sound.

6.7 Two inclined frictionless tracks, one gradual and the other steep, meet at A from where two stones are allowed to slide down from rest, one on each track as shown in Fig. 6.1.

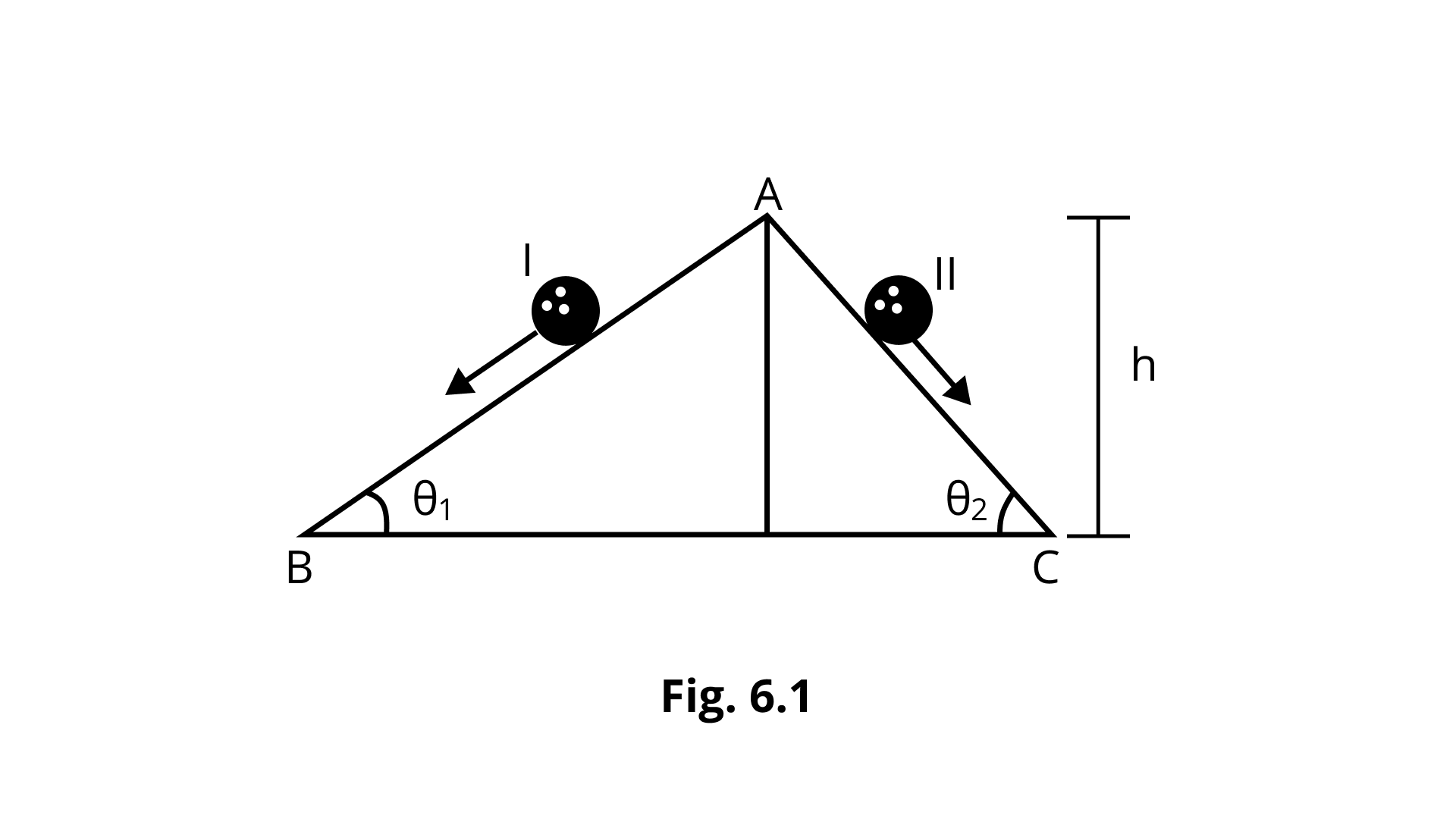
Which of the following statements is correct?

(a) Both the stones reach the bottom at the same time but not with the same speed.

(b) Both the stones reach the bottom with the same speed and stone I reaches the bottom earlier than stone II.

(c) Both the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.

(d) Both the stones reach the bottom at different times and with different speeds.

Ans: (c) obtion is correct.

As seen in the diagrams, A B and A C are two smooth planes inclined at the angles ${\theta _1}$ and ${\theta _2}$, respectively. 

Because there is no friction here, mechanical energy will be preserved. 

Because both tracks have the same height h,

$\frac{1}{2}m{v^2} = mg$

$hv = \sqrt {2gh}$ 

Hence, speed is the same for both stones. For stone $I,{a_1} =$ acceleration along inclined plane = g sin ${\theta _1}$

Similarly, for stone II, ${a_2} = g\sin {\theta _2}$

And because track II is shorter in length, stone II arrives earlier than stone I.

6.8 The potential energy function for a particle executing linear SHM is given by $V(x) = \frac{1}{2}k{x^2}$ where k is the force constant of the oscillator (Fig. 6.2). For$k = 0.5{\text{N}}/{\text{m}}$, the graph of $V(x)$ versus $x$ is shown in the figure. A particle of total energy E turns back when it reaches$x =  \pm {x_m}$. If V and K indicate the P.E. and K.E., respectively of the particle at $x =  + {x_m}$, then which of the following is correct?

(a) $\quad V = {\text{O}},\quad K = E$

(b) $\quad V = E,\quad K = {\text{O}}$

(c) $\quad V < E,\quad K = {\text{O}}$

(d) $\quad V = {\text{O}},\quad K < E$

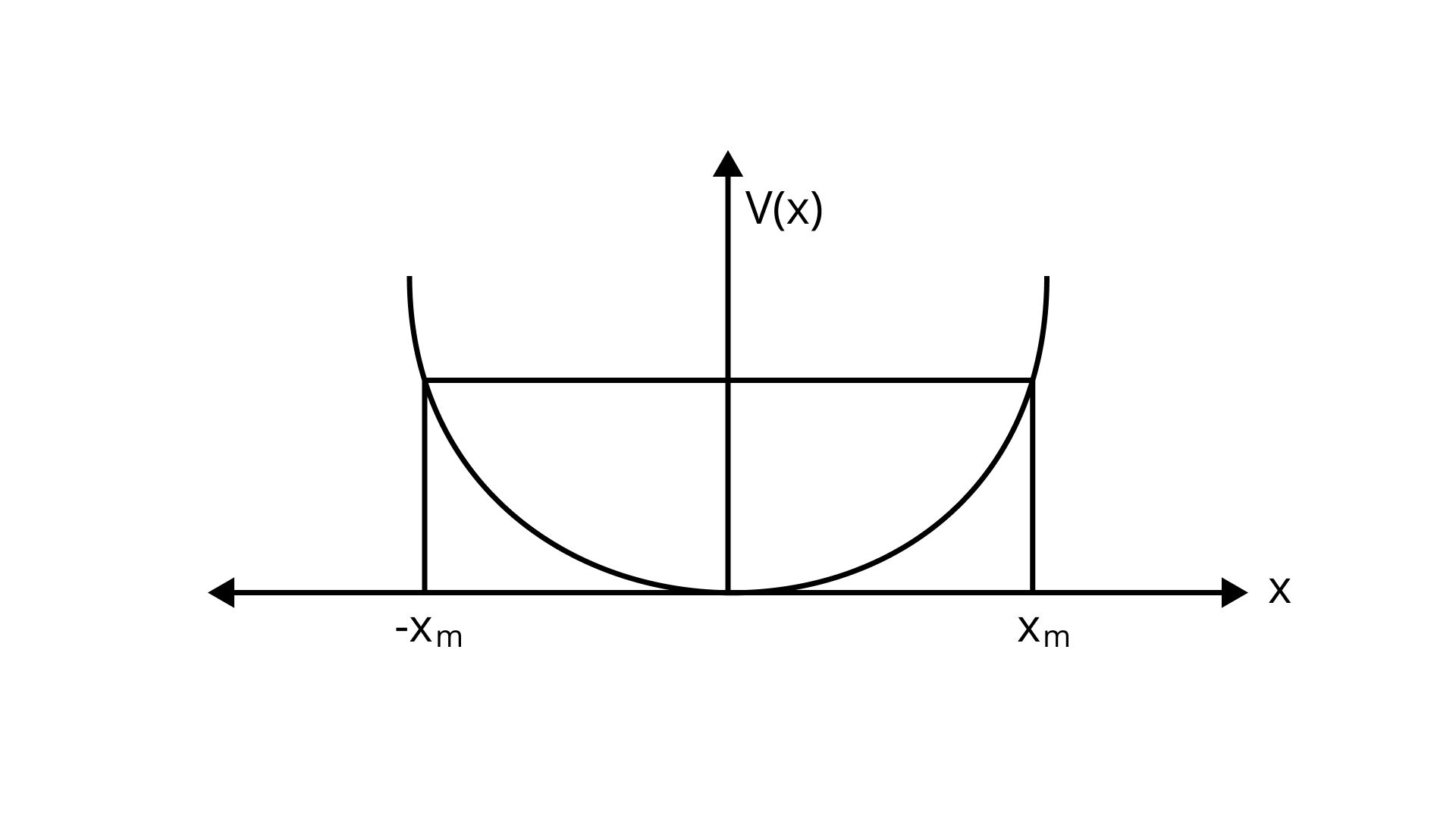
Ans: (b) obtion is correct.

$U = \frac{1}{2}k{x^2}$

For extreame position,

$U = \frac{1}{2}k{a^2}$

Total Energy, $E = \frac{1}{2}k{a^2}$

$K = \frac{1}{2}m{v^2} = 0$

At any position, K.E., $K = E - U = \frac{1}{2}k{a^2} - \frac{1}{2}k{x^2}$

$K = \frac{1}{2}k\left( {{a^2} - {x^2}} \right)$

Total energy,

$E = {\text{PE}} + 0 = {\text{PE}} \Rightarrow V\left( {{x_m}} \right) = \frac{1}{2}kx_m^2$

As a result, $\quad V = E,\quad K = {\text{O}}$

6.9 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in Fig. 6.3.

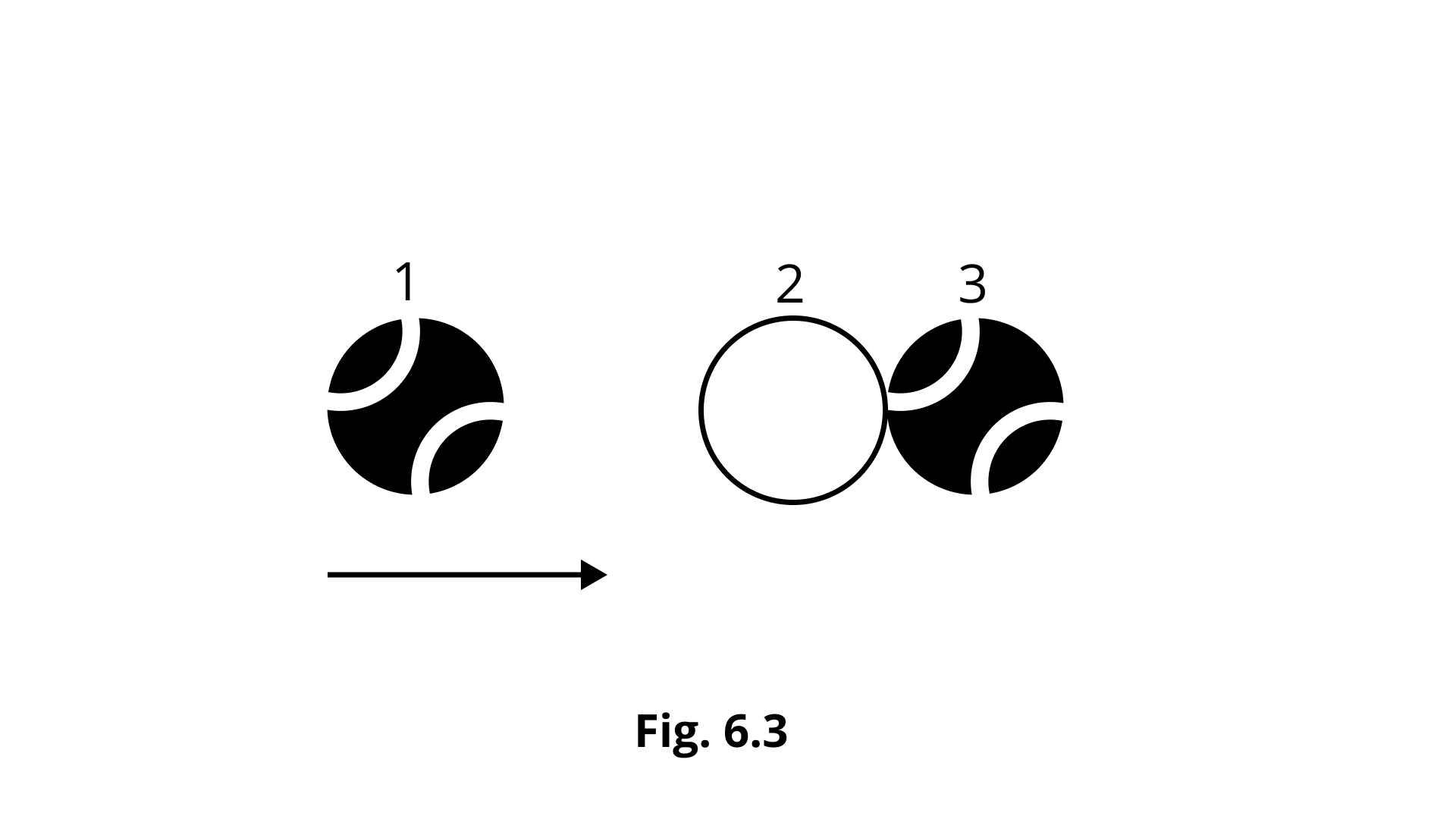
If the collision is elastic, which of the following (Fig. 6.4) is a possible result after collision?

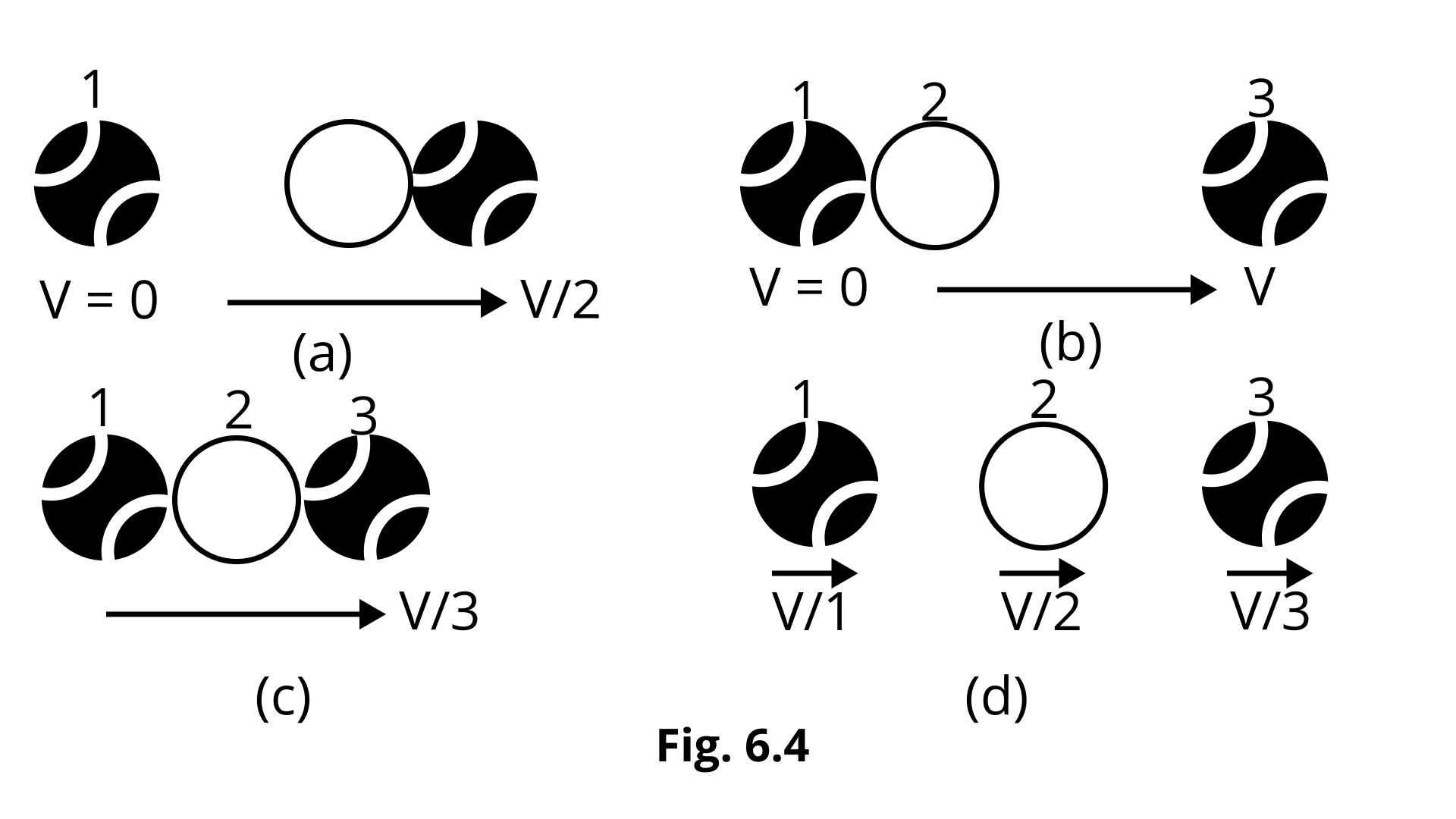
Ans: (b) obtion is correct.

${K_2} = \frac{1}{2}(m){(v)^2} = \frac{1}{2}m{v^2}$

6.10 A body of mass $0.5{\text{kg}}$ travels in a straight line with velocity $v = a{x^{3/2}}$ where$a = 5{{\text{m}}^{ - 1/2}}{{\text{s}}^{ - 1}}$. The work done by the net force during its displacement from $x = 0$ to $x = 2{\text{m}}$ is

(a) $1.5{\text{J}}$

(b) $50{\text{J}}$

(c) $10{\text{J}}$

(d) $100{\text{J}}$

Ans: (b) obtion is correct.

$W = \int_A^B {\vec F}  \cdot d\vec s...(i)$

$W = \int_{{x_1}}^{{x_2}} {{f_x}} dx + \int_{{y_1}}^{{y_2}} {{f_y}} dy + \int_{{z_1}}^{{z_2}} {{f_z}} dz...(ii)$

${a_0} = \frac{{dv}}{{dt}} = v\frac{{dv}}{{dx}}$

$= a{x^{3/2}}\frac{d}{{dx}}\left( {a{x^{3/2}}} \right)$

$= a{x^{3/2}} \times a \times \frac{3}{2} \times {x^{1/2}} = \frac{3}{2}{a^2}{x^2}$ 

$m{a_0} = m\left( {\frac{3}{2}{a^2}{x^2}} \right)$

Work done,

$= \int_{x = 0}^{x = 2} F dx = \int_0^2 {\frac{3}{2}} m{a^2}{x^2}dx$

$= \frac{3}{2}m{a^2} \times \left( {\frac{{{x^3}}}{3}} \right)_0^2$

$= \frac{1}{2}m{a^2} \times 8 = \frac{1}{2} \times (0.5) \times (25) \times 8$

$= 50{\text{J}}$ 

6.11 A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in Fig. 6.5 correctly shows the displacement-time curve for its motion?

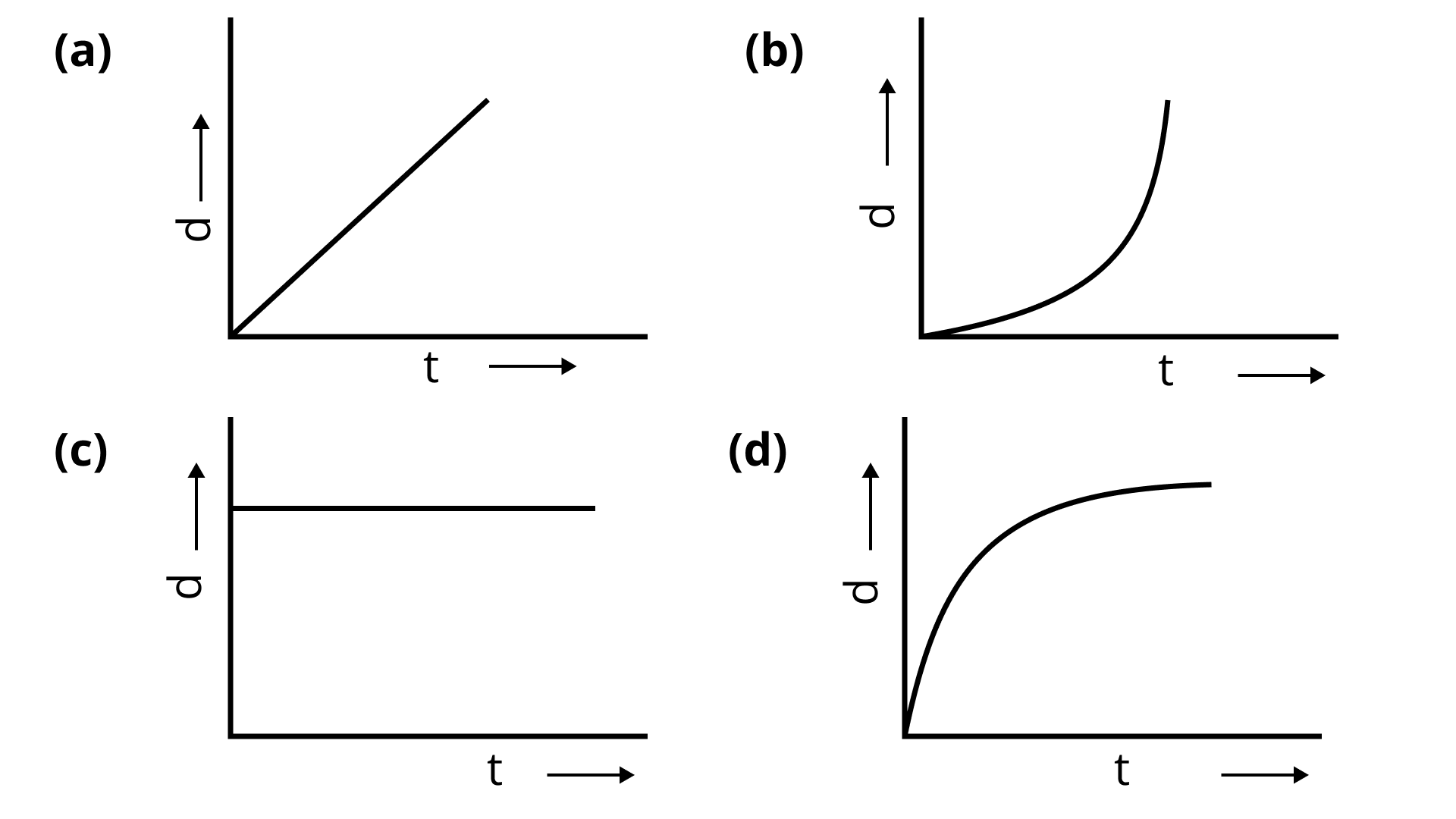
Ans: (b) obtion is correct.

For constant power Displacement $\propto {t^{3/2}}$

As

$P = \frac{{\vec F \cdot d\vec s}}{{dt}} = \vec F \cdot \vec v = {\text{ constant }}$

because P= constant according to the problem

Now, will by dimensional analysis

$[F][v] =$constant

$\Rightarrow \left[ {ML{T^{ - 2}}} \right]\left[ {L{T^{ - 1}}} \right] =$constant

$\Rightarrow {L^2}{T^{ - 3}} =$constant (because mass is constant )

$\Rightarrow \quad L \propto {T^{3/2}}$

$\Rightarrow Displacement(d) \propto {t^{3/2}}$

6.12 Which of the diagrams shown in Fig. 6.6 most closely shows the variation in kinetic energy of the earth as it moves once around the sun in its elliptical orbit? 

Ans: (d) obtion is correct.

Because the earth rotates once around the sun in its elliptical orbit, the speed of the earth is greatest when it is closest to the sun, and hence KE is greatest. 

When the earth is the furthest away from the sun, the speed is the slowest, hence K E is the slowest, but it is never 0 or negative.

6.13 Which of the diagrams shown in Fig. 6.7 represents variation of total mechanical energy of a pendulum oscillating in air as function of time?

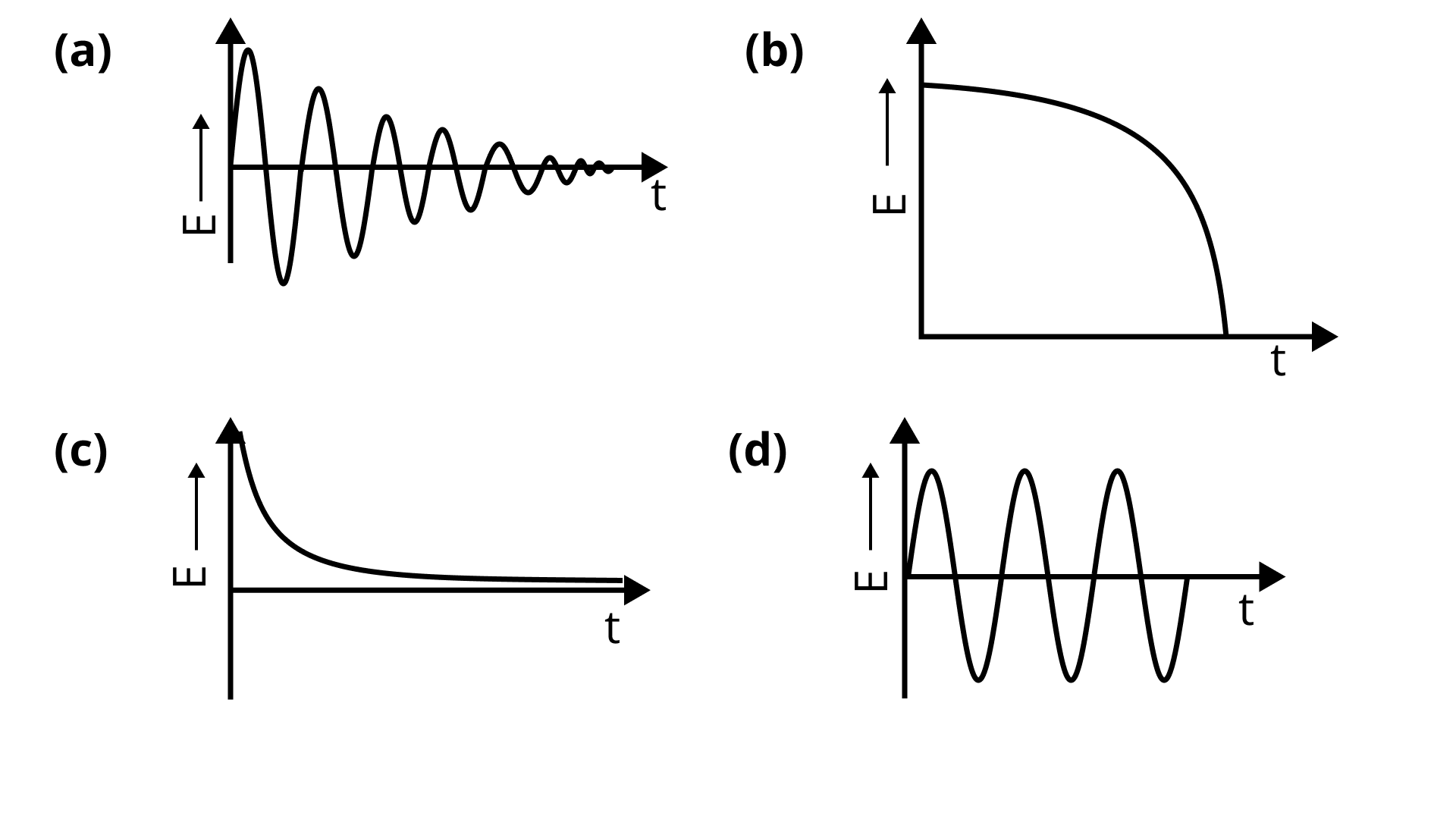
Ans: (c) option is correct.

When a pendulum oscillates in air, its total mechanical energy gradually falls as it overcomes air resistance. 

As a result, the pendulum's total mechanical energy drops exponentially over time.

6.14 A mass of $5{\text{kg}}$ is moving along a circular path of radius$1{\text{m}}$. If the mass moves with $[{\mathbf{300}}]$ revolutions per minute, its kinetic energy would be

(a) $250{\pi ^2}$

(b) $100{\pi ^2}$

(c) $5{\pi ^2}$

(d) $[{\mathbf{0}}]$

Ans: (a) option is correct.

Radius$= 1\ {\text{m}}$, mass $= m = 5{\text{kg}}$

$f = 300{\text{rev}}/{\text{min}}$

$f = \frac{{300}}{{60}}$

Angular Velocity, 

$= 2\pi f = (300 \times 2\pi ){\text{rad}}/{\text{min}}$

$= (300 \times 2 \times 3.14){\text{rad}}/60{\text{s}}$

$= \frac{{300 \times 2 \times 3.14}}{{60}}{\text{rad}}/{\text{s}}$

$= 10\pi {\text{rad}}/{\text{s}}$ 

Now, $\nu  = \omega R$

$= \left( {\frac{{300 \times 2\pi }}{{60}}} \right)(1{\text{m}})$

$= 10\pi {\text{m}}/{\text{s}}$ 

K.E.,

$= \frac{1}{2}m{v^2} = \frac{1}{2} \times 5 \times {(10\pi )^2}$

$\Rightarrow 100{\pi ^2} \times 5 \times \frac{1}{2} = 250{\pi ^2}{\text{J}}$ 

6.15 A raindrop falling from a height h above ground, attains a near terminal velocity when it has fallen through a height $(3/4)h$. Which of the diagrams shown in Fig. 6.8 correctly shows the change in kinetic and potential energy of the drop during its fall up to the ground?

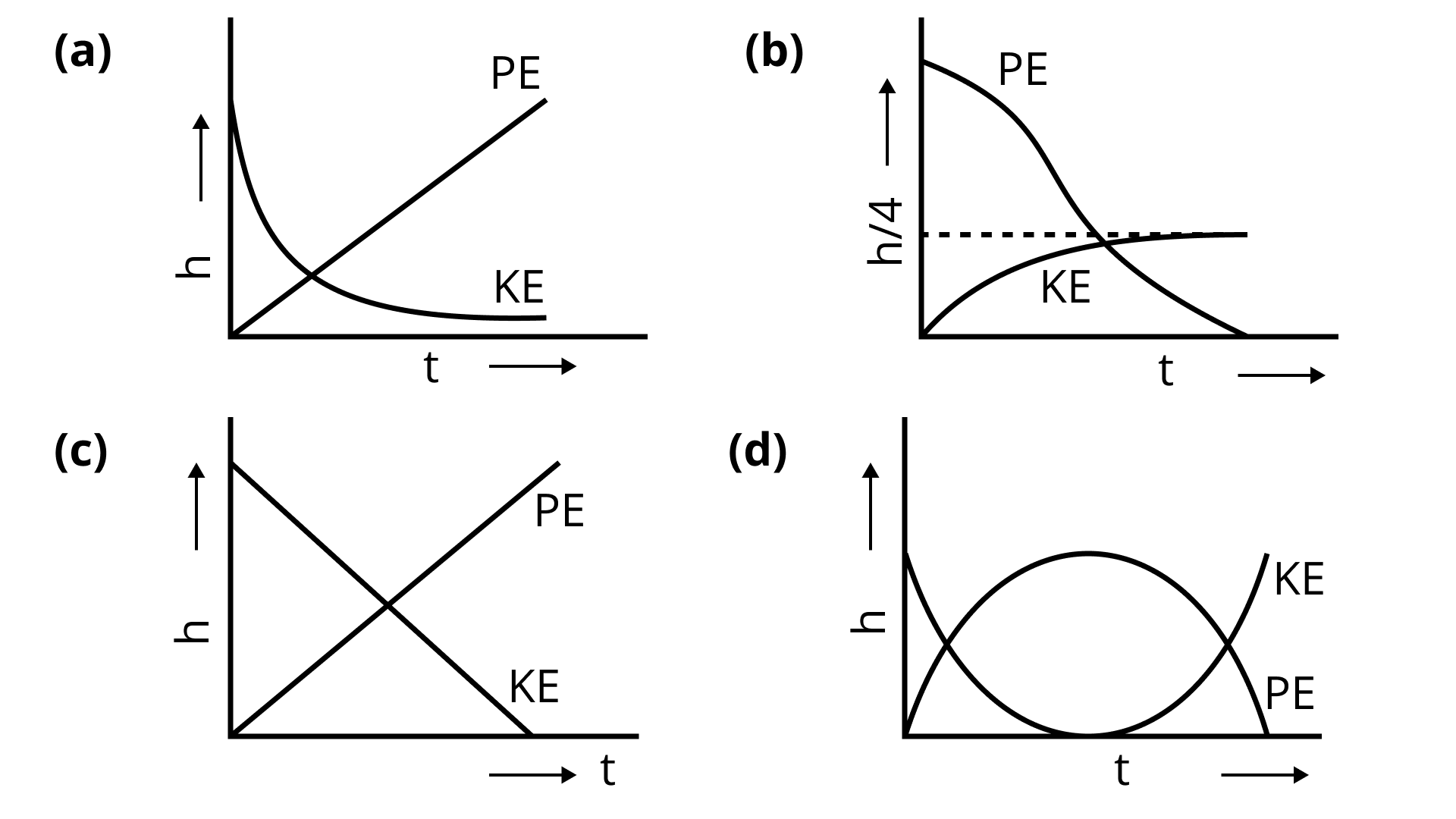
Ans: (d) obtion is correct.

If air resistance is minimal, the system's total mechanical energy remains constant. 

And let us use ground as a reference point where potential energy is zero.

$h = 1.5{\text{m}},{\text{v}} = 1{\text{m}}/{\text{s}},{\text{m}} = 10{\text{kg}},{\text{g}} = 10{\text{m}}{{\text{s}}^{ - 2}}$

Initial Energy,

$= {({\text{PE}})_i} + {({\text{KE}})_i}$

$= mgh + \frac{1}{2}m{v^2}$

$= 10 \times 10 \times 1.5 + \frac{1}{2} \times 10 \times {(1)^2}$

$= 150 + 5$

$= 155{\text{J}}$ 

${({\text{PE}})_i} + {({\text{KE}})_i} = {({\text{PE}})_f} + {({\text{KE}})_f}$

$155{J_{}} = 0 + {({\text{KE}})_f}$ 

Final K.E. $= 155J$

6.16 In a shotput event an athlete throws the shotput of mass $10{\text{kg}}$ with an initial speed of $1{\text{m}}{{\text{s}}^{ - 1}}$ at ${45^\circ }$ from a height $1.5{\text{m}}$ above ground. Assuming air resistance to be negligible and acceleration due to gravity to be$10{\text{m}}{{\text{s}}^{ - 2}}$, the kinetic energy of the shotput when it just reaches the ground will be

(a) $2.5{\text{J}}$

(b) $5.0{\text{J}}$

(c) $52.5{\text{J}}$

(d) $155.0{\text{J}}$

Ans: (b) obtion is correct.

When an iron sphere falls freely in a lake, it is accelerated by gravity, and its velocity rises continually while resistance from the water causes a force known as viscous force or upthrust (in fluids), which opposes its motion. 

It is determined by the velocity of the item; as the velocity increases, so does the upthrust. 

As a result, during the fall of a sphere, its velocity increases at first and then becomes constant at some depth.This constant velocity is referred to as terminal velocity, and it follows that K. E becomes constant beyond this depth, which is best illustrated as (b).

6.17 Which of the diagrams in Fig. 6.9 correctly shows the change in kinetic energy of an iron sphere falling freely in a lake having sufficient depth to impart it a terminal velocity?

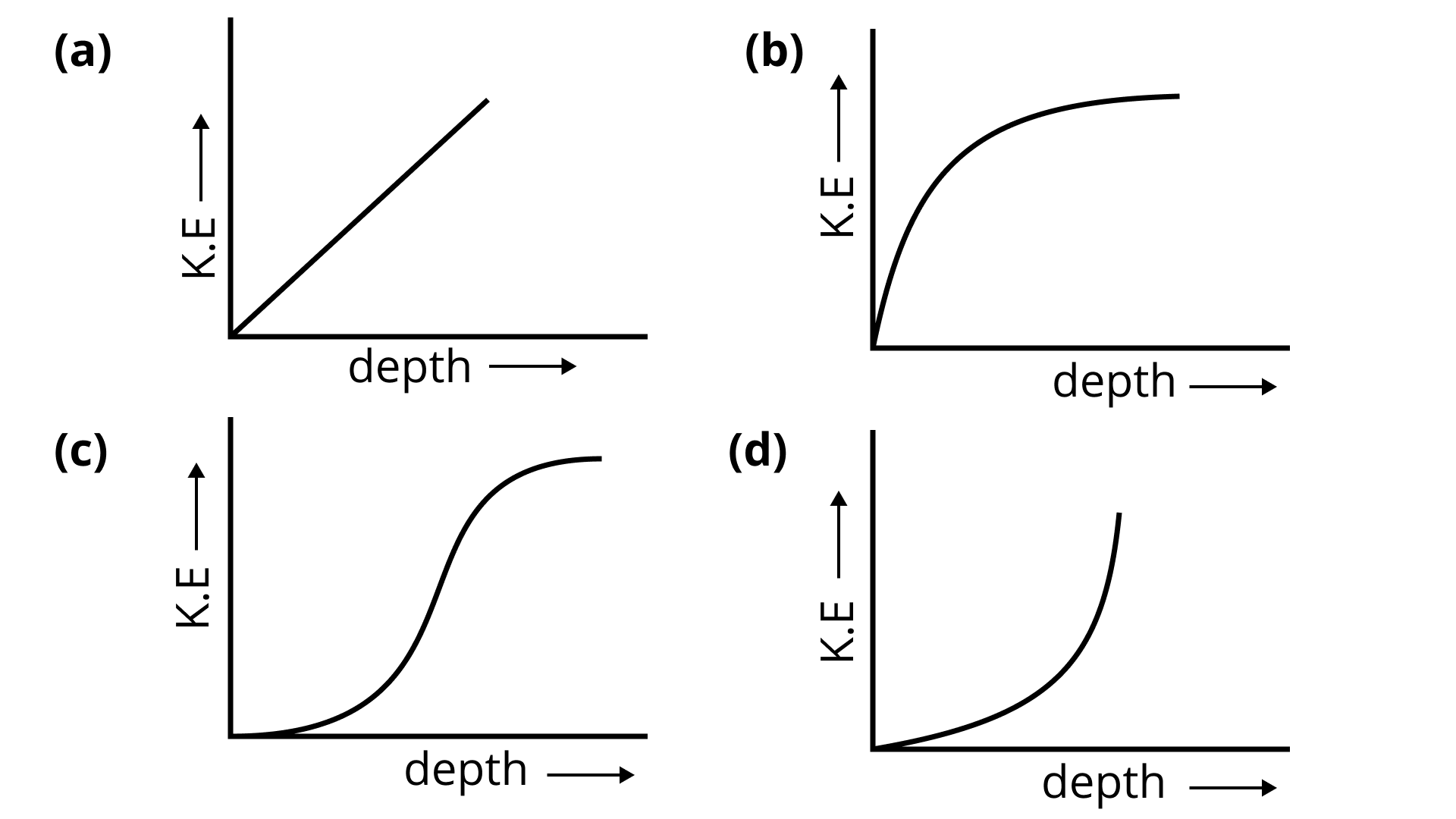
Ans: (b) obtion is correct.

When an iron sphere falls freely in a lake, it is accelerated by gravity, and its velocity rises continually as a result of resistance from the water, which causes a force known as viscous force or upthrus (in fluids) to oppose its motion. 

It is determined by the velocity of the item; as the velocity increases, so does the upthrust. As a result, during the fall of a sphere, its velocity increases at first and then becomes constant at some depth.

This constant velocity is referred to as terminal velocity, and it follows that KE becomes constant beyond this depth, which is best illustrated by (b).

6.18 A cricket ball of mass $150{\text{g}}$ moving with a speed of $126{\text{km}}/{\text{h}}$ hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remain in contact for $0.001$s, the force that the batsman had to apply to hold the bat firmly at its place would be

(a) $10.5{\text{N}}$

(b) $21{\text{N}}$

(c) $1.05 \times {10^4}{\text{N}}$

(d) $2.1 \times {10^4}{\text{N}}$

Ans: (c) obtion is correct.

$F = \frac{{\Delta p}}{{\Delta t}}{\text{ }}$

$\frac{{\Delta p}}{{\Delta t}} = \frac{{m[( - v) - u]}}{t} = \frac{{ - 2mv}}{t}$ 

Magnitude of force, $F = \frac{{2mv}}{t}$

$m = 150{\text{g}} = \frac{{150}}{{1000}}{\text{kg}} = \frac{3}{{20}}{\text{kg}}$

$\Delta t = {\text{ time of contact }} = 0.001{\text{s}}$

$u = 126{\text{km}}/{\text{h}} = \frac{{126 \times 1000}}{{60 \times 60}}{\text{m}}/{\text{s}} = 35{\text{m}}/{\text{s}}$

$v =  - 126{\text{km}}/{\text{h}} =  - 35{\text{m}}/{\text{s}}$ 

Change in Momentum,

$\Delta p = m(v - u)$

$= \frac{3}{{20}}( - 35 - 35){\text{kg}} - {\text{m}}/{\text{s}}$

$= \frac{3}{{20}}( - 70)$

$=  - \frac{{21}}{2}$ 

$F = \frac{{\Delta p}}{{\Delta t}} = \frac{{ - 21/2}}{{0.001}}{\text{N}}$

$=  - 1.05 \times {10^4}{\text{N}}$ 

MCQ II

6.19 A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.

(a) Work done by all forces on man is equal to the rise in potential energy mgL.

(b) Work done by all forces on man is zero.

(c) Work done by the gravitational force on man is mgL.

(d) The reaction force from a step does not do work because the point of application of the force does not move while the force exists.

Ans: Obtions (b) and (d) are correct.

Obtion (b) is correct because

Work Done by gravitational force on man$ = $ -mgL 

The effort done by man to pull himself up by muscular force will be in the displacement direction as the force provided by muscles  $ = $ +mgL

So net Work Done = -mgL + mgL = 0.

Obtion (d) is correct because there is no displacement point where the reaction acts so, 

Work Done by reaction torce$ = 0$. 

As the person's velocity approaches zero at the peak.

So KE $ = 0$. 

Hence , Work Done is zero.

6.20 A bullet of mass m fired at ${30^{^\circ }}$ to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerges out with half the kinetic energy it had before hitting the target.

Which of the following statements are correct in respect of a bullet after it emerges out of the target?

(a) The velocity of the bullet will be reduced to half its initial value.

Ans: Assume that 

$K{E_1}$ =  kinetic energy of the bullet before hitting the target.

$K{E_2} =$ kinetic energy of the bullet after hitting the target.

$1K{E_2} = \frac{1}{2}K{E_1}$

$\frac{1}{2}mv_2^2 = \frac{1}{2} \cdot \frac{1}{2}mv_1^2$

$v_2^2 = \frac{1}{2}v_1^2 = {\left( {\frac{{{v_1}}}{{\sqrt 2 }}} \right)^2} = {\left( {\frac{{{v_1}\sqrt 2 }}{2}} \right)^2} = {\left( {.707{v_1}} \right)^2}$ 

\[{{\text{v}}_{\text{2}}}{\text{ =  0}}{\text{.707 }}{{\text{v}}_{\text{1}}}\]

As a result, the bullet's velocity after hitting the target is not reduced by half. So, this obtion is incorrect.

(b) The velocity of the bullet will be more than half of its earlier velocity.

Ans: \[{{\text{v}}_{\text{2}}}{\text{ =  0}}{\text{.707 }}{{\text{v}}_{\text{1}}}\]

As a result, the bullet's velocity after hitting the target is more than half of its initial velocity. So, this obtion is correct.

(c) The bullet will continue to move along the same parabolic path.

Ans: This obtion is incorrect, Because the bullet has a horizontal velocity, its route will be parabolic, but with fresh parabolas as both components and alterations after it exits the target.

(d) The bullet will move in a different parabolic path.

Ans: This obtion is correct, As previously explained, the path of the bullet after hitting the target will be a new parabola.

(e) The bullet will fall vertically downward after hitting the target.

Ans: This obtion is incorrect, 

Because the bullet comprises horizontal and vertical components, the new parabola has a lowerrange than the previous one.

(f) The internal energy of the particles of the target will increase.

Ans: This obtion is correct,

As some of the bullet's kinetic energy was transformed into heat, the target's internal energy rose.

6.21 Two blocks ${M_1}$ and ${M_2}$ having equal mass are free to move on a horizontal frictionless surface. ${{\text{M}}_2}$ is attached to a massless spring as shown in Fig. 6.10. Iniially ${M_2}$ is at rest and ${M_1}$ is moving toward ${M_2}$ with speed v and collides head-on with ${M_2}$.

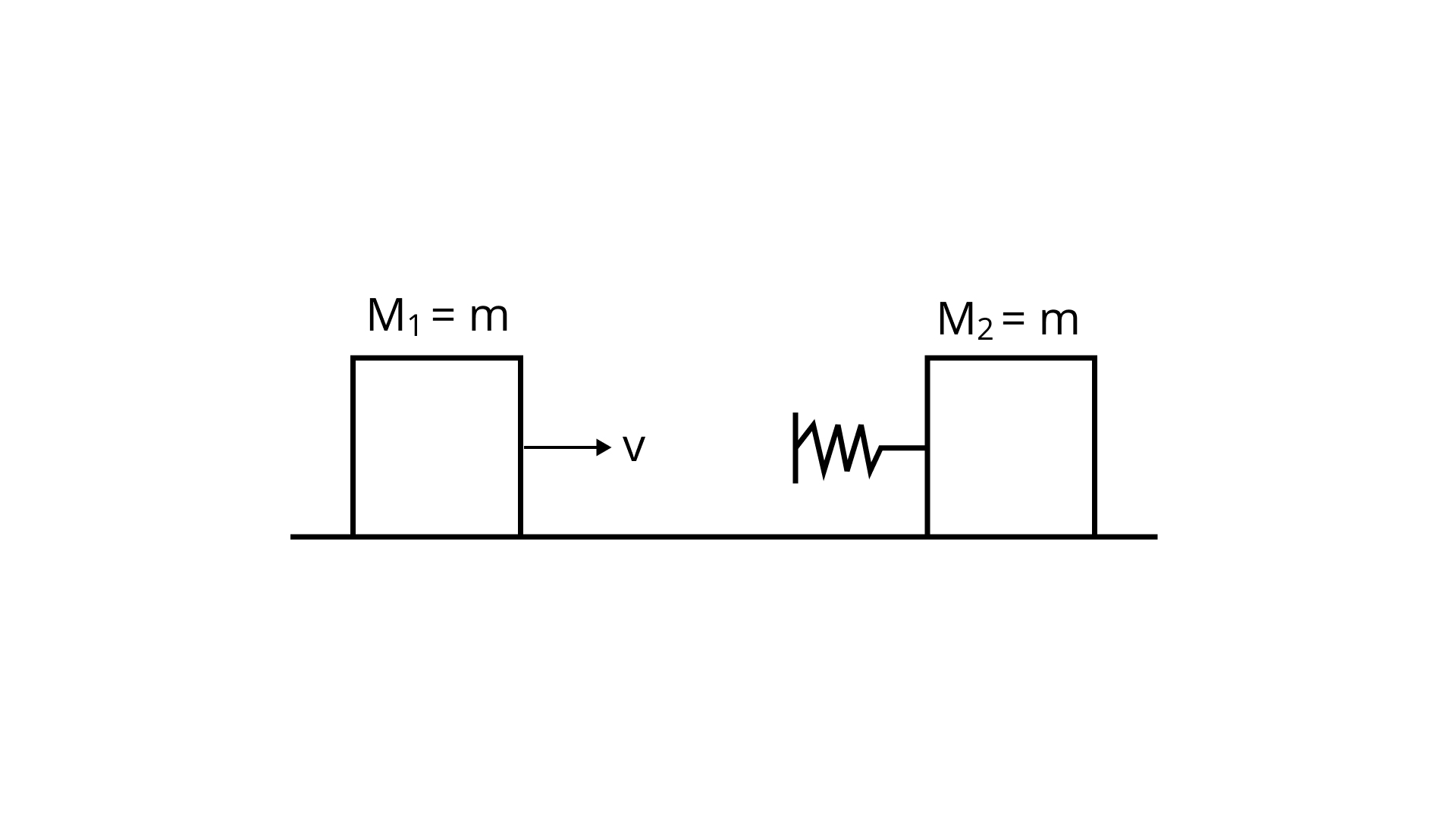
(a) While spring is fully compressed all the KE of ${M_1}$ is stored as PE of spring.

Ans: This is incorrect because,

The spring's whole KE of ${M_1}$is not communicated to the spring's PE.

(b) While spring is fully compressed the system momentum is not conserved, though final momentum is equal to initial momentum.

Ans: This is incorrect because surfaces have little friction. 

As a result, the law of conservation of mass applies.

(c) If spring is massless, the final state of the${M_1}$ is a state of rest.

Ans: This is correct because

If the spring has no mass, the entire KE of ${M_1}$ is transferred to ${M_2}$ which then travels with velocity v before coming to rest. Because surfaces have a low coefficient of friction. As a result, the law of mass conservation applies.

(d) If the surface on which blocks are moving has friction, then collision cannot be elastic.

Ans: This is incorrect because collision is inelastic even if no frictional force is involved.

VSA

6.22 A rough inclined plane is placed on a cart moving with a constant velocity u on horizontal ground. A block of mass M rests on the incline. Is any work done by force of friction between the block and incline? Is there then a dissipation of energy?

Ans: As,$f = Mg\sin \theta $

The friction force on the body is caused by the propensity of the block M to slide \[Mgsin\theta\] down across the inclined plane. Because block has no displacement, the work done by f and block is zero. 

There is no energy dissipation since there is no labour.

6.23 Why is electrical power required at all when the elevator is descending? Why should there be a limit on the number of passengers in this case?

Ans: When the elevator lowers, 

it is not free fall under gravity; instead, it drops at a constant speed. 

To reduce the velocity caused by free fall, power is necessary.

The power of an elevator's motor or system is continuous, and a restricted or predetermined power can stop the speed of freely dropping passengers along with the elevator.

6.24 A body is being raised to a height h from the surface of earth. What is the sign of work done by

(a) applied force

Ans: Work done by applied force is positive.

$WD = \vec Fd\bar s = Fds\cos \theta $

$\Rightarrow Fds\cos {0^\circ } = Fds\cos \theta $

$\theta  = {0^\circ }$ 

(b) gravitational force?

Ans: Work done by gravitational force is negative.

${\text{WD}} = {\text{Fds}}\cos {180^\circ } =  - {\text{Fds}}$

Because Gravitional force always acts towards the ground.

6.25 Calculate the work done by a car against gravity in moving along a straight horizontal road. The mass of the car is $400{\text{kg}}$ and the distance moved is$2{\text{m}}$.

Ans: As $WD = Fs\cos \theta$

Because the angle formed by horizontal distance $2m$ and gravity vertically downward is $90\degree$.

$WD = Fs\cos {90^\circ } = 0$

So the work done by the automobile against gravity is zero.

6.26 A body falls towards earth in air. Will its total mechanical energy be conserved during the fall? Justify.

Ans: For a body that is free to fall under the influence of gravity. 

Mechanical energy is not conserved because some of it is used to overcome the force offriction between air molecules, which is a non-conservative force.

However, if a body falls freely under gravity in a vacuum, the total mechanical energy remains constant.

6.27 A body is moved along a closed loop. Is the work done in moving the body necessarily zero? If not, state the condition under which work done over a closed path is always zero.

Ans: If only conservative force acts on the body during motion, 

the work done by a body travelling around a closed loop can be zero.

Work done by a body travelling around a loop is not zero if the body is subjected to any non-conservative force, such as friction, electrostatic, or magnetic force.

6.28 In an elastic collision of two billiard balls, which of the following quantities remain conserved during the short time of collision of the balls (i.e., when they are in contact). Give reason for your answer in each case.

(a) Kinetic energy.

Ans: When two billiard balls meet, their kinetic energy is preserved. 

Because it is assumed that there is no nonconservative force (such as air resistance/surface friction, etc.) and the speed of the ball is not so great that it deforms on contact.

(b) Total linear momentum?

Ans: When two billiard balls meet, their linear momentum is preserved. 

Because it is assumed that there is no nonconservative force (such as air resistance/surface friction, etc.) and the speed of the ball is not so great that it deforms on contact.

6.29 Calculate the power of a crane in watts, which lifts a mass of $100{\text{kg}}$ to a height of $10{\text{m}}$ in $20{\text{s}}$.

Ans: $P = \frac{{WD}}{{{\text{ time }}}} = \frac{{F \cdot s\cos \theta }}{t} = \frac{{mg \cdot h\cos \theta }}{t}$

$\theta  = {0^\circ }$

$F = mg$

$= 100 \times 10\quad $

$h = 10m\quad t = 20s$ 

$\therefore P = \frac{{100 \times 10 \times 10\cos {0^\circ }}}{{20}} = 500{\text{Watts}}$

6.30 The average work done by a human heart while it beats once is\[{\mathbf{0}}.{\mathbf{5}}{\text{ }}{\mathbf{J}}\]. Calculate the power used by the heart if it beats \[{\mathbf{72}}\] times in a minute.

Ans: $P = \frac{{W \cdot D}}{{{\text{ time }}}}$

W.D in 1 heartbeat $ = 0.5{\text{J}}$

W.D in 72 heartbeats $ = 0.5 \times 72 = 36{\text{J}}$

Time $ = 1$minute $ = 60{\text{s}}$

$\therefore P = \frac{{WD}}{t} = \frac{{36}}{{60}} = \frac{6}{{10}} = 0.6{\text{W}}$

As a result, the power consumed by the heart is $0.6{\text{W}}$.

6.31 Give an example of a situation in which an applied force does not result in a change in kinetic energy.

Ans: ${\text{WD}} = {\text{F}} \cdot {\text{s}}\cos \theta $

Work Done (WD) will be zero in this circumstance if the angle between force and displacement is \[90\degree\].

For example, 

(i)If a body moves horizontally with homogeneous motion, the WD by gravity is zero.

(ii) Work completed while moving in a circular manner.

(iii) When the direction of motion of a charge particle is perpendicular to the magnetic field, the direction of force owing to the magnetic field is perpendicular to both the direction of motion of the charge and the magnetic field, according to Fleming's left hand rule.

As a result, the magnetic field does no work on the charge particle.

6.32 Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying a retarding force of the same magnitude. How would the distance moved by them before coming to rest compare?

Ans: According to WE Theorem,

$K{E_1} = K{E_2}({\text{As stated}})$

$W{D_1} = W{D_2}$

${F_1}{s_1} = {F_2}{s_2}$

$\because {F_1} = {F_2}{\text{ (As stated) }}$

$\therefore {s_1} = {s_2}$ 

As a result, both bodies will travel the same displacement or distance (it does not depend on mass of bodies).

6.33 A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in Fig. 6.11. What will be the trajectory of the particle if the string is cut at

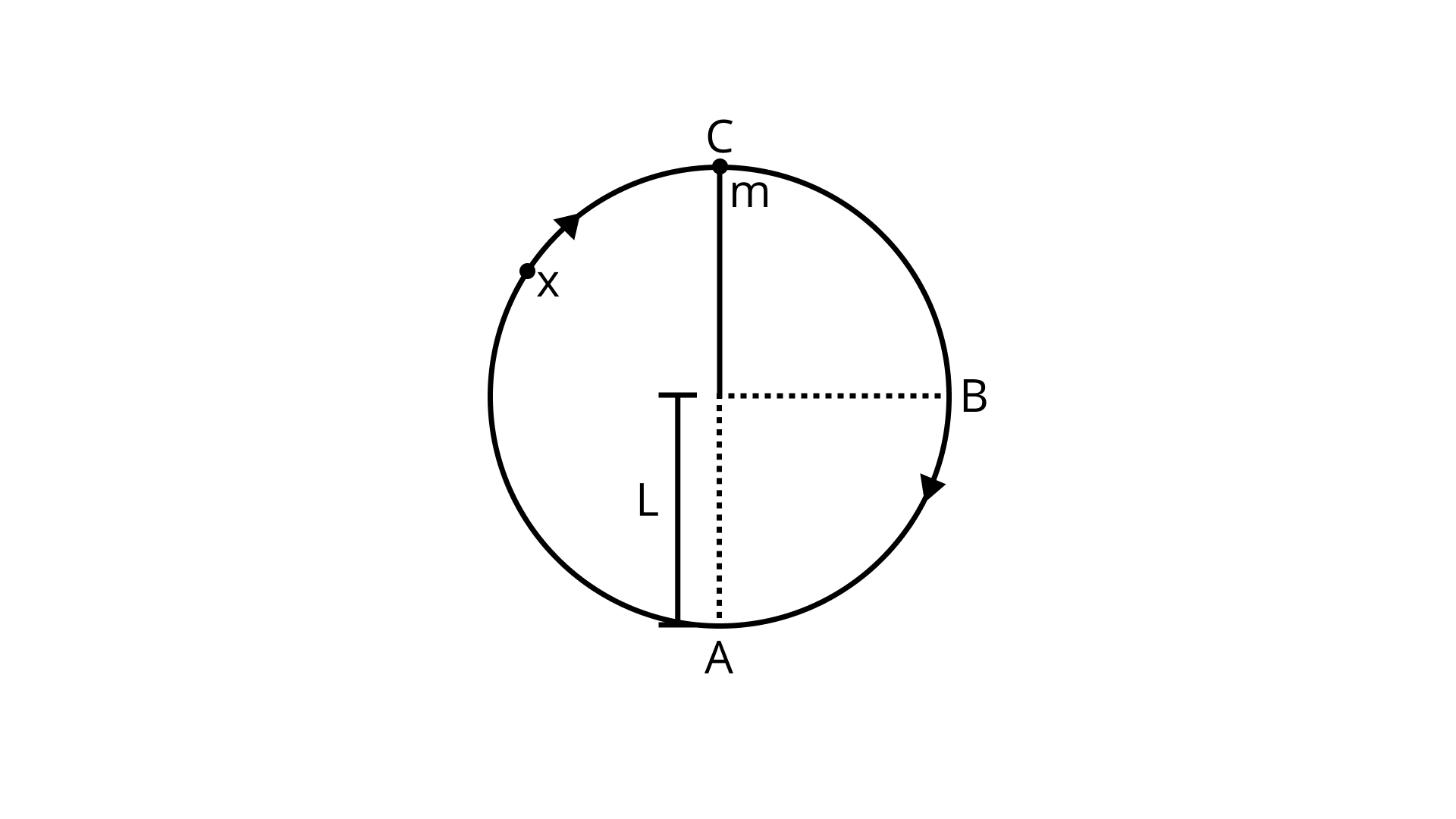
(a) Point B?

Ans: If the thread is severed at B, 

the tangential velocity is vertically downward, 

As a result, bob will travel vertically under gravity.

(b) Point C?

Ans:If the string is severed at C, bob will move along a half-parabolic route, as illustrated in the picture.

(c) Point X?

Ans: If the string is severed at X, the velocity of the bob produces an angle $\theta$ with the horizontal, causing it to proceed on a parabolic route that reaches a greater height and then returns to a parabolic path.

SA

6.34 A graph of potential energy $V(x)$ versus $x$ is shown in Fig. 6.12. A particle of energy ${E_0}$ is executing motion in it. Draw graph of 

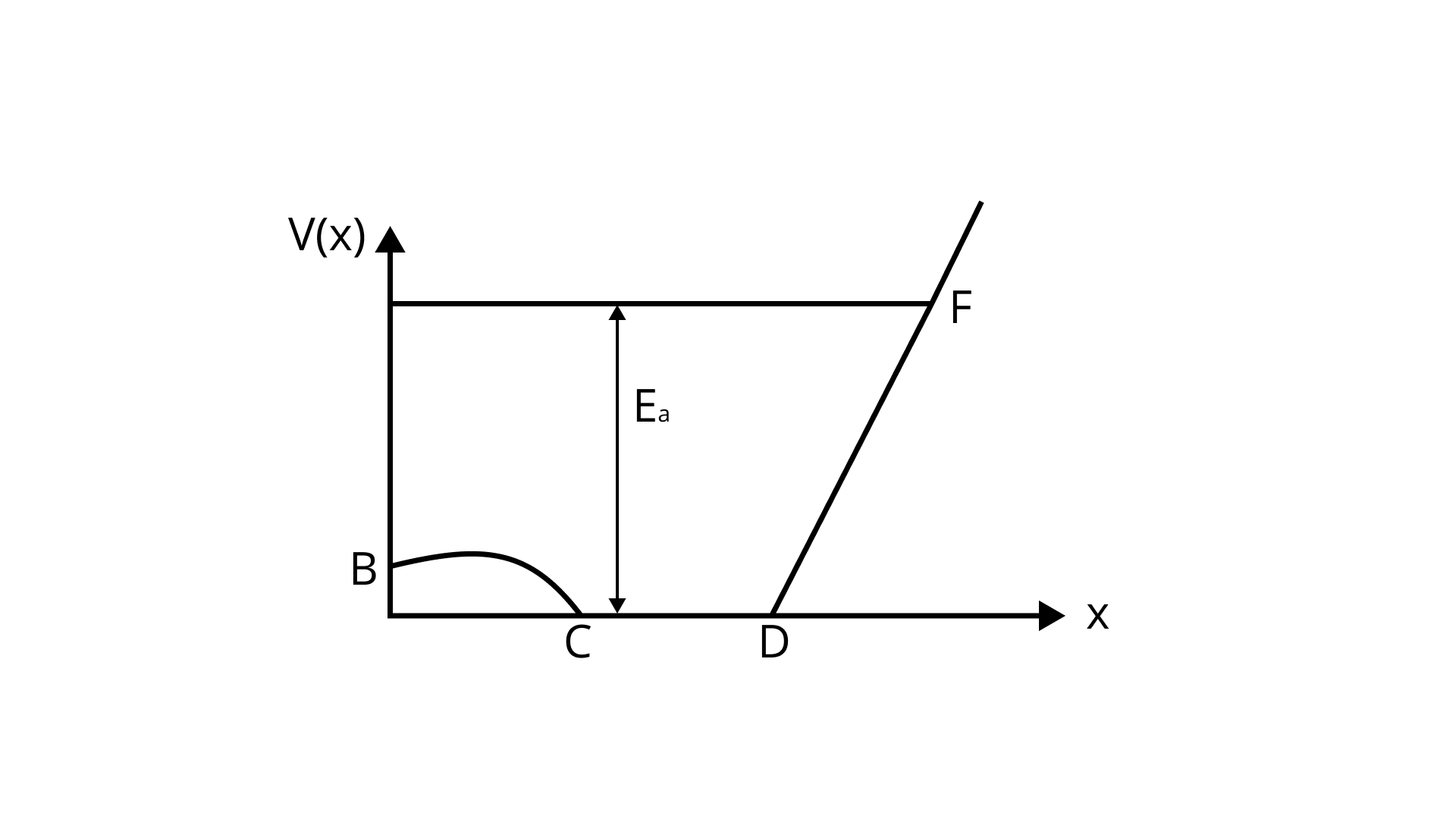
(i) velocity versus $x$ for one complete cycle AFA.

Ans:

$KE =  - mv$

$v = \sqrt {\frac{{2K}}{m}} $

$v = \sqrt K $ 

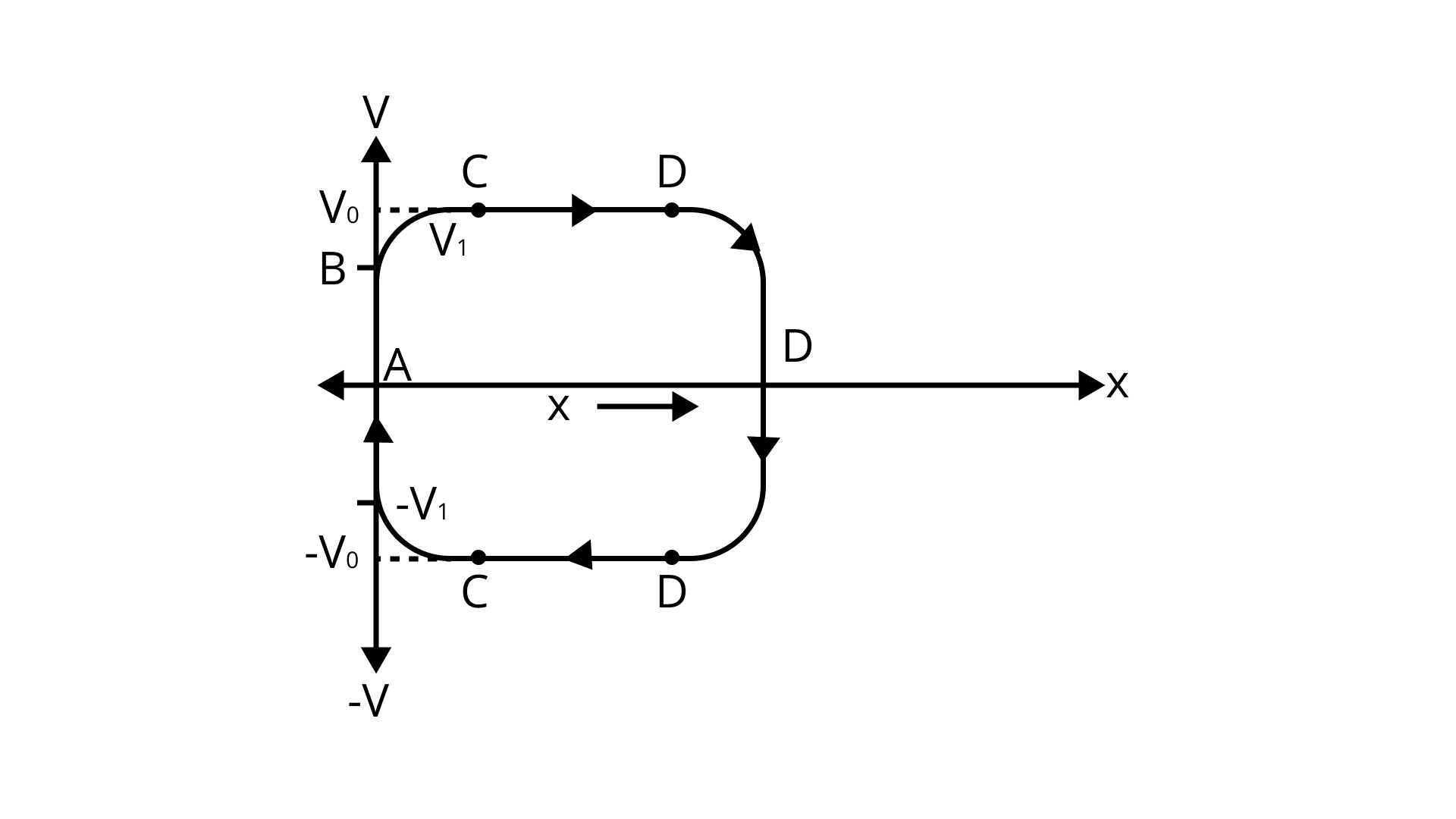
At Point A & F,

${\text{KE}} = 0{x_A} = 0,{x_D} = {x_3}$

At C & D

${x_c} = {x_1},{x_D} = {x_2}$

$KE = {E_0}n$

$\therefore {v_{\max }} =  \pm \sqrt {{E_0}}  = {v_0}$

$\therefore {\text{ At B, }}x = 0\quad KE = {E_1}$

$\therefore {v_B} = \sqrt {{E_1}}  =  \pm v$ 

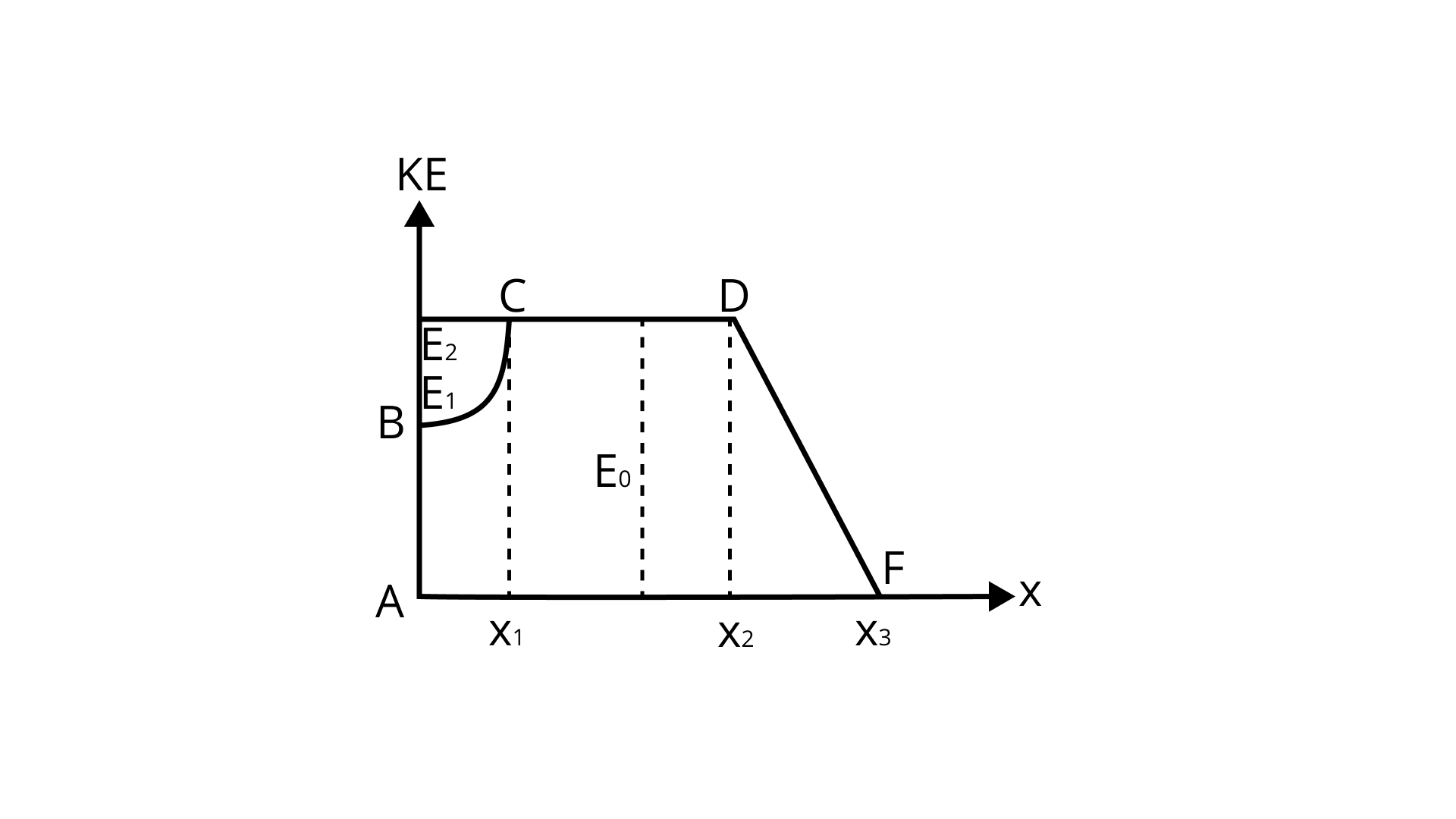
(ii) kinetic energy versus $x$ for one complete cycle AFA.

Ans: kinetic energy versus $x$

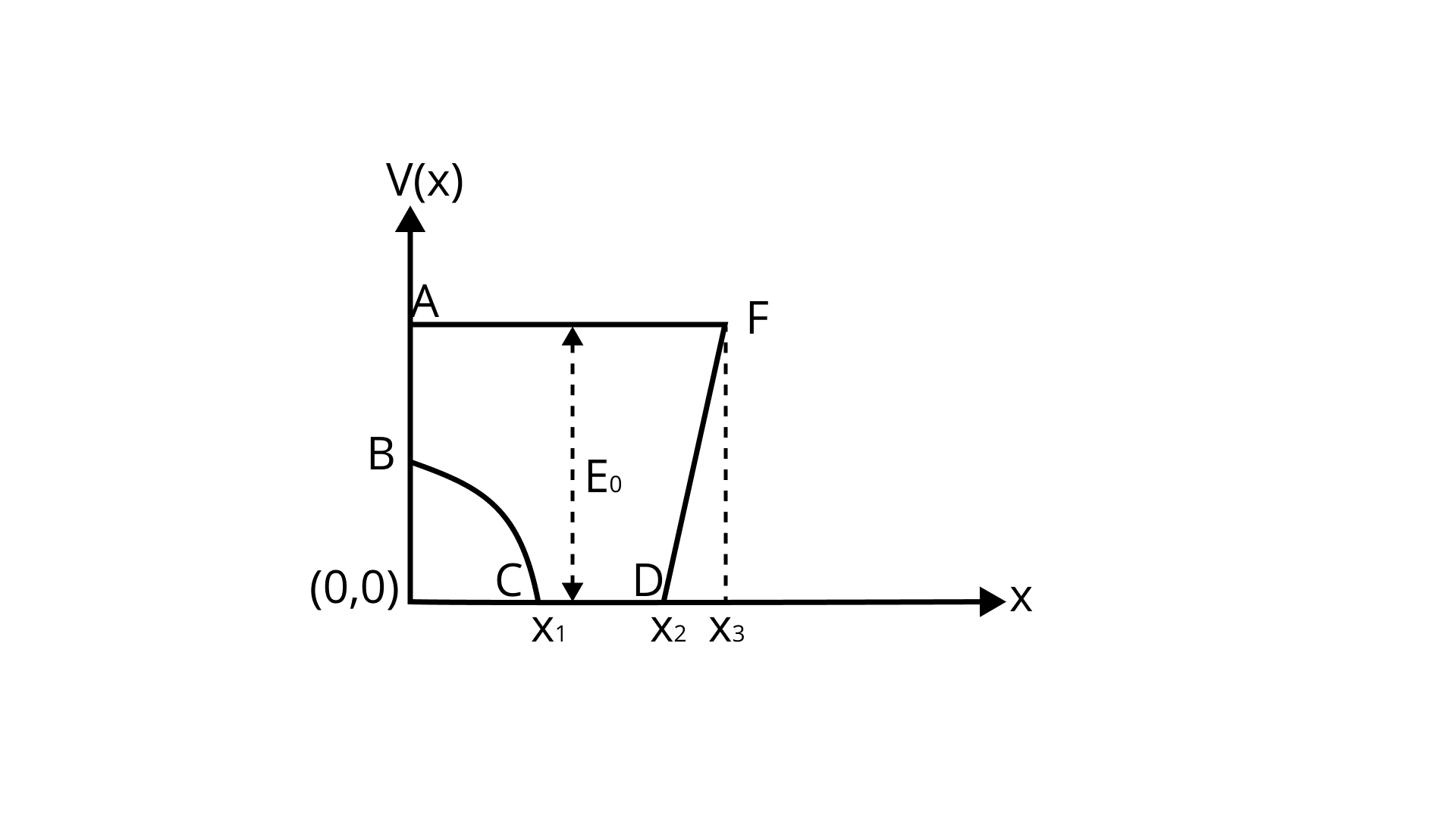
Using Law of Conservation of Energy:

$E = KE + PE$

${E_0} = KE + V(x)$

$K \cdot E \cdot {E_0} - V(x)$ 

PE is at its highest at point A.

$PE = {E_0}\quad \therefore KE = {E_0} - {E_0} = 0$

At B,

${\text{x}} = 0$

$PE = {V_B}$

$KE = {E_0} - {V_0}$ 

At C,

$x = {x_1}PE = 0$

$\therefore \quad KE = {E_0} - V(x) = {E_0} - 0 = {E_0}{\text{ }}$ 

At D, 

${\text{x}} = {{\text{x}}_2}{\text{KE}} = {{\text{E}}_0}$

At E,

$x = {x_3}PE = {E_0}\therefore {\text{KE}} = 0$

6.35 A ball of mass m, moving with a speed $2{v_0}$,  collides inelastically $({\text{e}} > 0)$ with an identical ball at rest. Show that

(a) For head-on collision, both the balls move forward.

Ans: Assume that the velocities of the two balls after the collision are ${v_1}$and ${v_2}$respectively. Now, according to the concept of momentum conservation

$m{v_o} = m{v_1} + m{v_2}$

$2{v_0} = {v_1} + {v_2} \ldots ({\text{i}})$

$e = \frac{{{v_2} - {v_1}}}{{{v_0} + {v_0}}} \Rightarrow {v_2} - {v_1} = 2e{v_0}$

${v_2} = {v_1} + 2e{v_o}$ 

Using (i),

${v_1} =  - {v_2} + 2{v_0}$

${v_1} =  - {v_1} - 2e{v_0} + 2{v_0}$

$2{v_1} = 2{v_0} - 2e{v_0}$

${v_1} = {v_0}(1 - e)$

$\because e < 1$ 

As a result,${v_o}$is positive, the direction of is the same as ${v_o}$, or \[{v_1}\] is in the forward direction. 

(b) For a general collision, the angle between the two velocities of scattered balls is less than ${90^\circ }$.

Ans: 

Using the law of conservation of momentum,

$\vec p = {\vec p_1} + {\vec p_2}$

$\therefore K{E_i} > K{E_1} + K{E_2}$

$\frac{1}{2}m{v^2} + \frac{1}{2}m{(0)^2} > \frac{1}{2}mv_1^2 + \frac{1}{2}mv_2^2$

$\frac{{{p^2}}}{{2m}} > \frac{{p_1^2}}{{2m}} + \frac{{p_2^2}}{{2m}}$

$\therefore \quad {{\vec p}^2} > \vec p_1^2 + \vec p_2^2...(iii)$ 

If ${p^2} = p_1^2 + p_2^2$ then the angle between ${p_1}$ and ${p_2}$ is ${90^\circ }$.

Hence (iii) is true when the angle between ${p_1},{p_2}$ is less than ${90^\circ }$.

6.36 Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D in which the relation between potential energy V, kinetic energy (K) and State with reason in each case whether a particle can be found in the given region or not and total energy E is as given below: 

(i) Region A: $V > E$

Ans: ${\text{E}} = {\text{V}} + {\text{K}}$

${\text{K}} = {\text{E}} - {\text{V}}$ 

$\because V > E$

$K < 0{\text{ }}$ 

It is not possible.

(ii) Region B : $V < E$

Ans: $K = E - V$

$K > 0$ 

It is possible.

(iii) Region C: $K > E$

Ans: $V = E - K$

$\Rightarrow \quad V < 0$ 

It is possible.

(iv) Region D : $V > K$

Ans: 

${\text{K}} = {\text{E}} - {\text{V}}$

It is possible.

6.37 The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.13. Neglect the size of the bobs and assume the collision to be elastic.

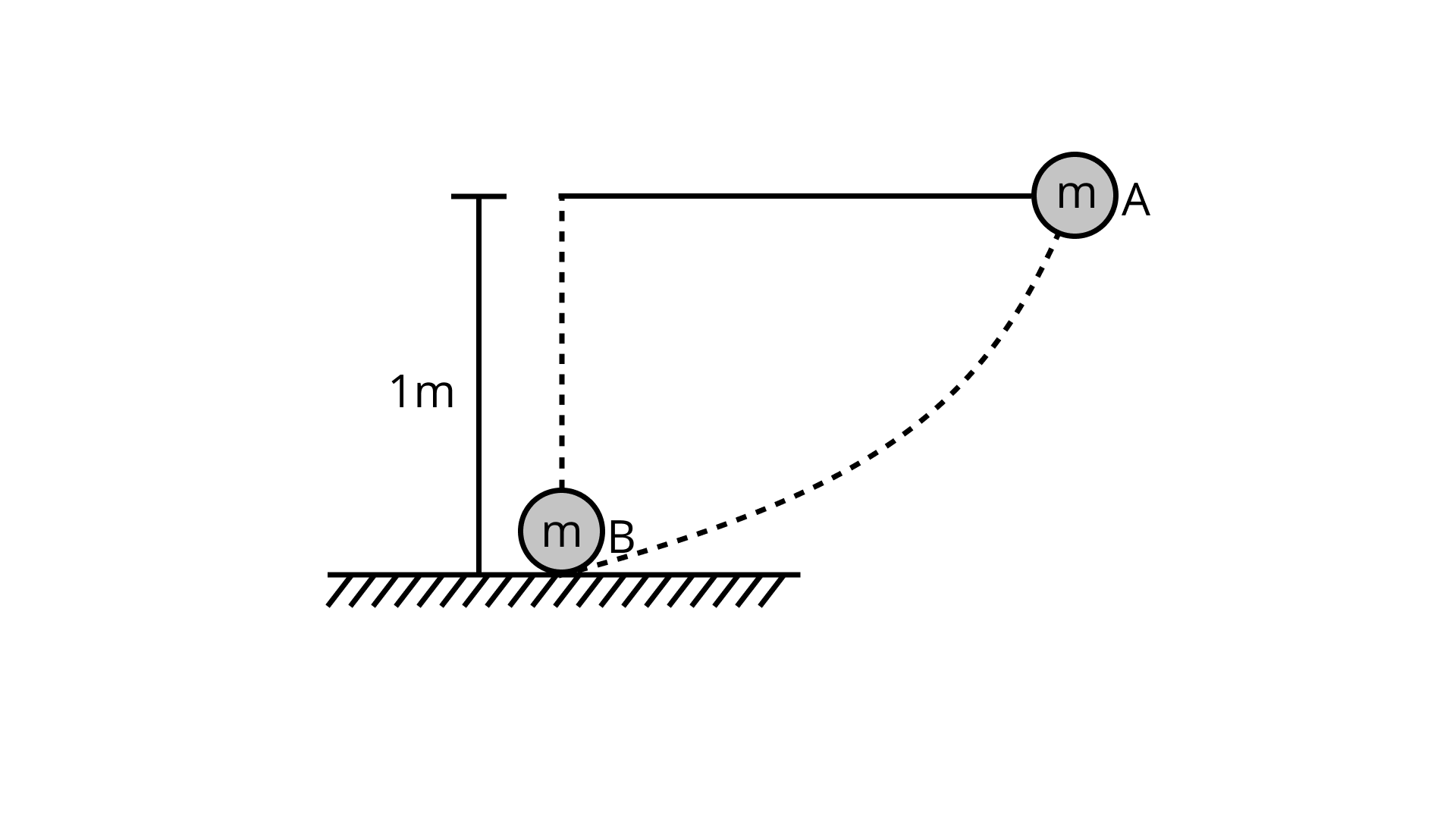
If the length of the pendulum is $1{\text{m}}$, calculate

(a) the height to which bob A will rise after collision.

Ans: When a moving bob collides with an identical bob at rest, the moving bob transfers its momentum to the other and becomes at rest. When Bob A reaches Bob B's position. After an elastic collision, the PE of A converts to KE, and bob A transfers its momentum to bob B, and bob A comes to rest. As a result, there will be no increase in bob A.

(b) the speed with which bob B starts moving.

Ans:

$P.{E_{ \cdot 4}} = K.{E_{ \cdot {A_2}}} = K.{E_{ \cdot B}}$

$\frac{1}{2}mv_b^2 = mgh$

${v_B} = \sqrt {2g \times 1} $

$= \sqrt {2 \times 9.8}  = \sqrt {\frac{2}{{10}} \times 2 \times 49} $

$= 2 \times 7\frac{1}{{\sqrt {10} }}$

$= \frac{{14 \times \sqrt {10} }}{{10}}$

$= 1.4 \times 3.16$

${v_B} = 4.42{\text{m}}/{\text{s}}$ 

6.38 A raindrop of mass $1.00{\text{g}}$ falling from a height of $1{\text{km}}$ hits the ground with a speed of $50{\text{m}}{{\text{s}}^{ - 1}}$. Calculate

(a) the loss of P.E. of the drop.

Ans: P.E. at highest point of drop $ = mgh = .001 \times 10 \times 1000 = 10{\text{J }}$

Loss of P.E. of the drop$ = 10{\text{J}}{\text{. }}$

(b) the gain in K.E. of the drop.

Ans: Gain in K.E $ = \frac{1}{2} \times 0.001 \times 50 \times 50 = 1.250$

(c) Is the gain in K.E. equal to loss of P.E.? If not why. Take $g = 10{\text{m}}{{\text{s}}^{ - 2}}$

Ans: The gain in KE does not match the loss in PE. 

It is caused by a loss of PE or KE in the face of air resistance or dragging force.

6.39 Two pendulums with identical bobs and lengths are suspended from a common support such that in the rest position the two bobs are in contact (Fig. 6.14). One of the bobs is released after being displaced by ${10^\circ }$ so that it collides elastically head-on with the other bob.

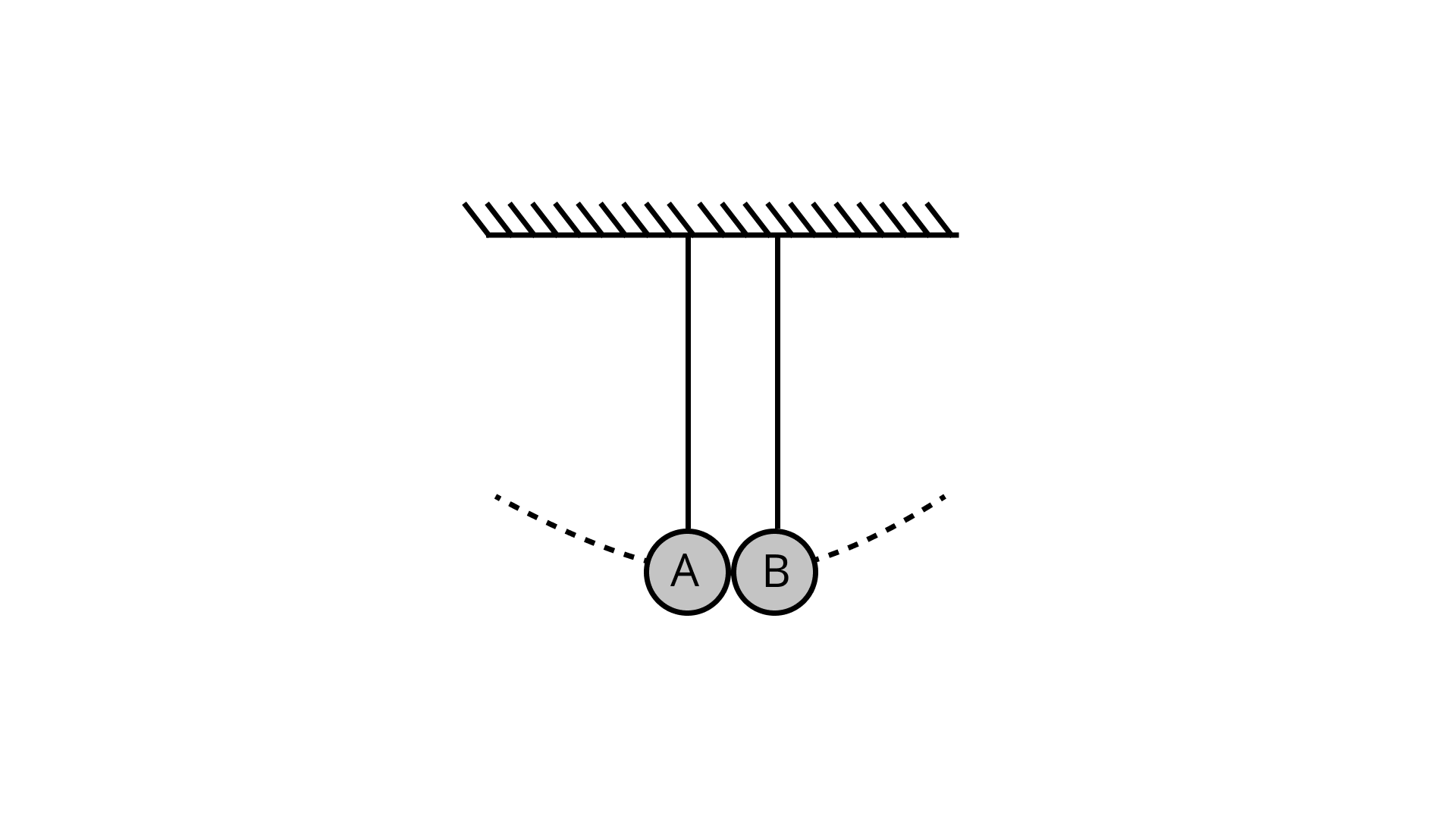
(a) Describe the motion of two bobs.

Ans: Assume, t = 0,

At A is at its lowest position, while B is at its highest position $10$ degree.

$P{E_A} = 0\quad P{E_B} = E,\quad K{E_A} = K{E_B} = 0$

$t = \dfrac{T}{4}B$  hits A and collides elastically since both bobs are identical, then

$K{E_A} = 0\quad K{E_B} = E,\quad P{E_A} = 0$

\[{\text{P }}{{\text{E}}_{\text{B}}}{\text{ = 0}}\]

$t = \dfrac{{2T}}{4}$ , A reaches its utmost height, whereas B remains at its lowest point.

$K{E_A} = 0\quad K{E_B} = 0,\quad P{E_A} = E,\quad P{E_B} = 0$

$t = \frac{{3T}}{4}$, Bob A elastically impacts bob B, which was at rest, and ball A becomes at rest, while B goes higher.

${{\text{K}}{{\text{E}}_{\text{A}}} = 0,}{{\text{K}}{{\text{E}}_{\text{B}}} = {\text{E}},\quad {\text{P}}{{\text{E}}_{\text{A}}} = 0,\quad {\text{P}}{{\text{E}}_{\text{B}}} = 0}$ 

${{E_A} = 0\quad }{{E_B} = E}$ 

$t = \frac{{4T}}{4}$, Bob B is at its tallest, while A is at its shortest.

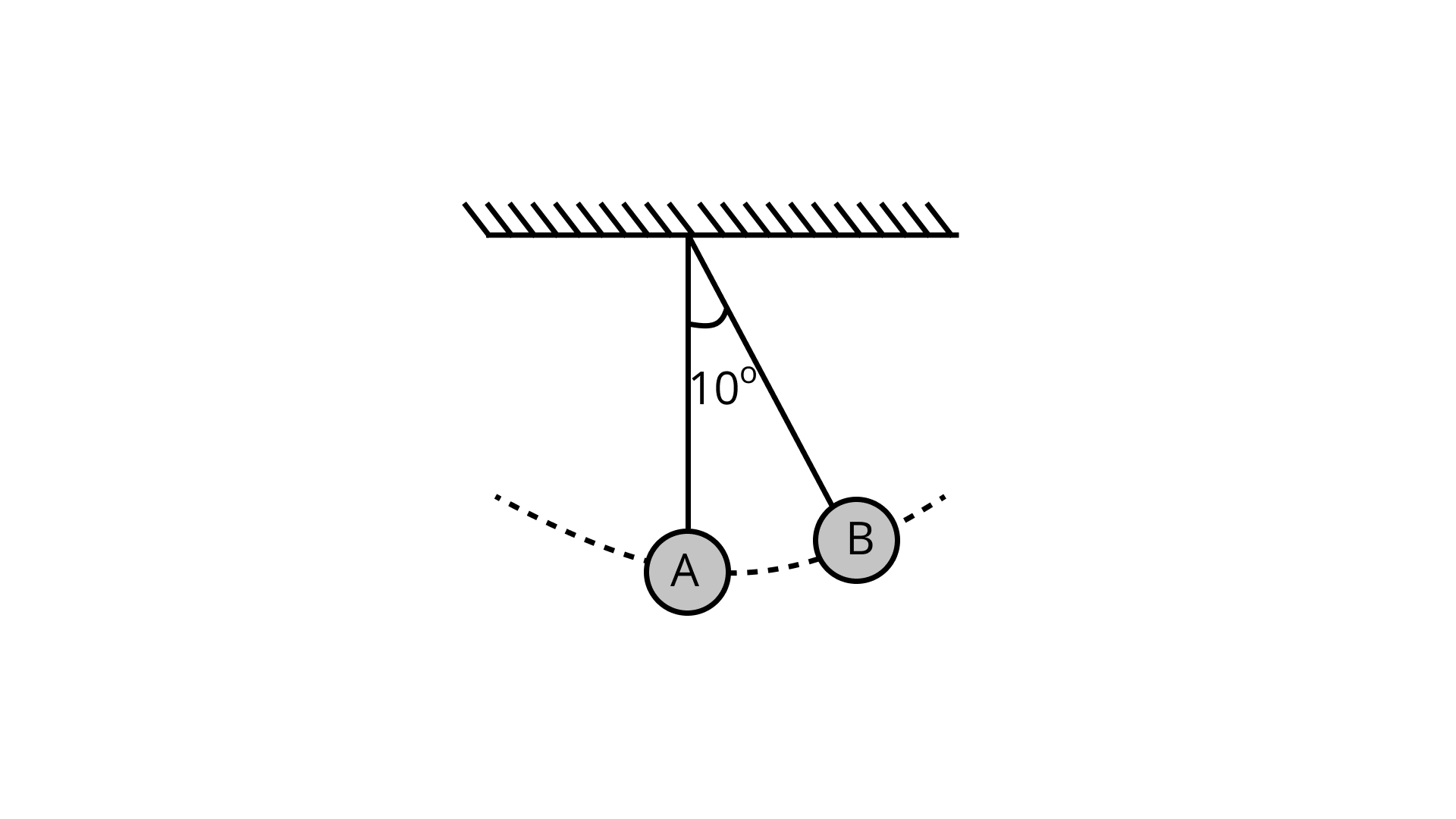
(b) Draw a graph showing variation in energy of either pendulum with time, for$0 \leqslant t \leqslant 2T$, where T is the period of each pendulum.

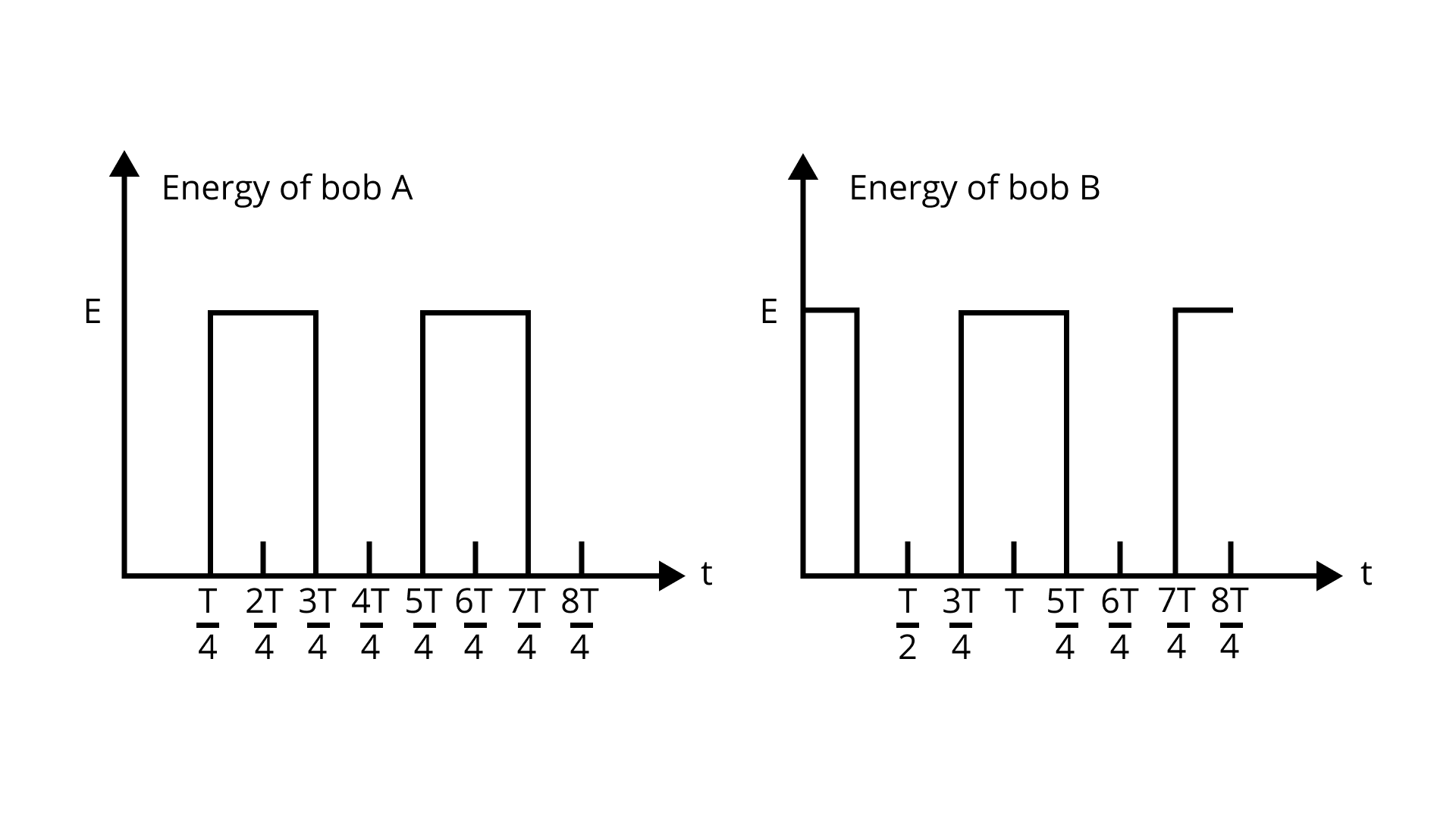
Ans: ${\text{K}}{{\text{E}}_{\text{A}}} = 0,\quad {\text{K}}{{\text{E}}_{\text{B}}} = 0,\quad {\text{P}}{{\text{E}}_{\text{A}}} = 0,\quad {\text{P}}{{\text{E}}_{\text{B}}} = {\text{E}}$

6.40 Suppose the average mass of raindrops is $3.0 \times {10^{ - 5}}{\text{kg}}$ and their average terminal velocity $9{\text{m}}{{\text{s}}^{ - 1}}$. Calculate the energy transferred by rain to each square metre of the surface at a place which receives $100{\text{cm}}$ of rain in a year.

Ans: The energy transmitted by rain to the earth's surface is kinetic energy$ = \frac{1}{2}m{v^2}$The speed of rain or water is 9 metres per second.

Mass $ = $ Volume $*$ Density

$ = $area of base $*$ height $*$ p

$= 1{m^2} \times 1m \times 1000$

$= 1000{\text{kg}}$ 

$E = \frac{1}{2}m{v^2}$

$= \frac{1}{2} \times 1000 \times 9 \times 9$

$= 500 \times 81$

$= 40500{\text{J}}$

$= 4.05 \times {10^4}{\text{J}}.$ 

6.41 An engine is attached to a wagon through a shock absorber of length$1.5{\text{m}}$. The system with a total mass of $50,000{\text{kg}}$ is moving with a speed of $36{\text{km}}{{\text{h}}^{ - 1}}$ when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by $1.0{\text{m}}$. If $90\% of energy of the wagon is lost due to friction, calculate the spring constant.

Ans: $KE = \frac{1}{2}m{v^2}\quad $

$m = 50,000{\text{kg}}$

$v = 36 \times \frac{5}{{18}}{\text{m}}/{\text{s}} = 10{\text{m}}/{\text{s}}$

$KE = \frac{1}{2} \times 50,000 \times 10 \times 10 = 2500000{\text{J}}$ 

K.E. of Spring $ = 10\% $of K.E. Wegon

$\frac{1}{2}k{x^2} = \frac{{10}}{{100}} \times 2500000x$

$= 1m\frac{1}{2}k \times 1 \times 1 = 250000{\text{K}}$

$= 500000 = 5 \times {10^5}{\text{N}}/{\text{m}}.$ 

6.42 An adult weighing $600{\text{N}}$ raises the centre of gravity of his body by $0.25{\text{m}}$ while taking each step of $1{\text{m}}$ length in jogging. If he jogs for $6{\text{km}}$, calculate the energy utilized by him in jogging assuming that there is no energy loss due to friction of ground and air. Assuming that the body of the adult is capable of converting $10\% $ of energy intake in the form of food, calculate the energy equivalents of food that would be required to compensate for energy utilised for jogging.

Ans:Energy expended by lifting the centre of gravity by \[0.25\]by jogging in a single step $ = mgh$

mg = 600N

$h = 0.25m$ 

No. of steps, $6{\text{Km}} = \frac{{6000{\text{m}}}}{{1{\text{m}}}} = 6000{\text{steps}}$

E in $6000{\text{m}} = 6000 \times 600 \times 0.25{\text{J}}$

$= \frac{{10}}{{100}} \times 6000 \times 600 \times 0.25$

$= 360000 \times 0.25$

$= 90000{\text{J}}$

$= 9 \times {10^4}{\text{J}}$ 

6.43 On complete combustion a litre of petrol gives off heat equivalent to$3 \times {10^7}{\text{J}}$. In a test drive a car weighing$1200{\text{kg}}$. Including the mass of the driver, runs $15{\text{km}}$ per litre while moving with a uniform speed on a straight track. Assuming that friction offered by the road surface and air to be uniform, calculate the force of friction acting on the car during the test drive, if the efficiency of the car engine were $0.5$.

Ans: Engine efficiency in automobiles $ = 0.5$

1 litre of gasoline provides 1 litre of energy to an automobile $ = 0.5 \times 3 \times {10^7}$

$ = 1.5 \times {10^7}$

Work done by car in $15{\text{km}} = {\text{ F}}{\text{.s }}$

$ = f \times 15000J\{ s = 15{\text{km}} = 15000{\text{m}}/l\} $

This labour done by the automobile is simply against the force of friction since the car is moving horizontally.

$f \times 15000 = 1.5 \times {10^7}$

$f = \frac{{1.5 \times {{10}^7}}}{{15000}} = {10^3}N$ 

LA

6.44 A block of mass $1{\text{kg}}$ is pushed up a surface inclined to horizontal at an angle of ${30^\circ }$ by a force of $10{\text{N}}$ parallel to the inclined surface (Fig. 6.15).The coefficient of friction between block and the incline is $0.1$. If the block is pushed up by $10{\text{m}}$ along the incline, calulate

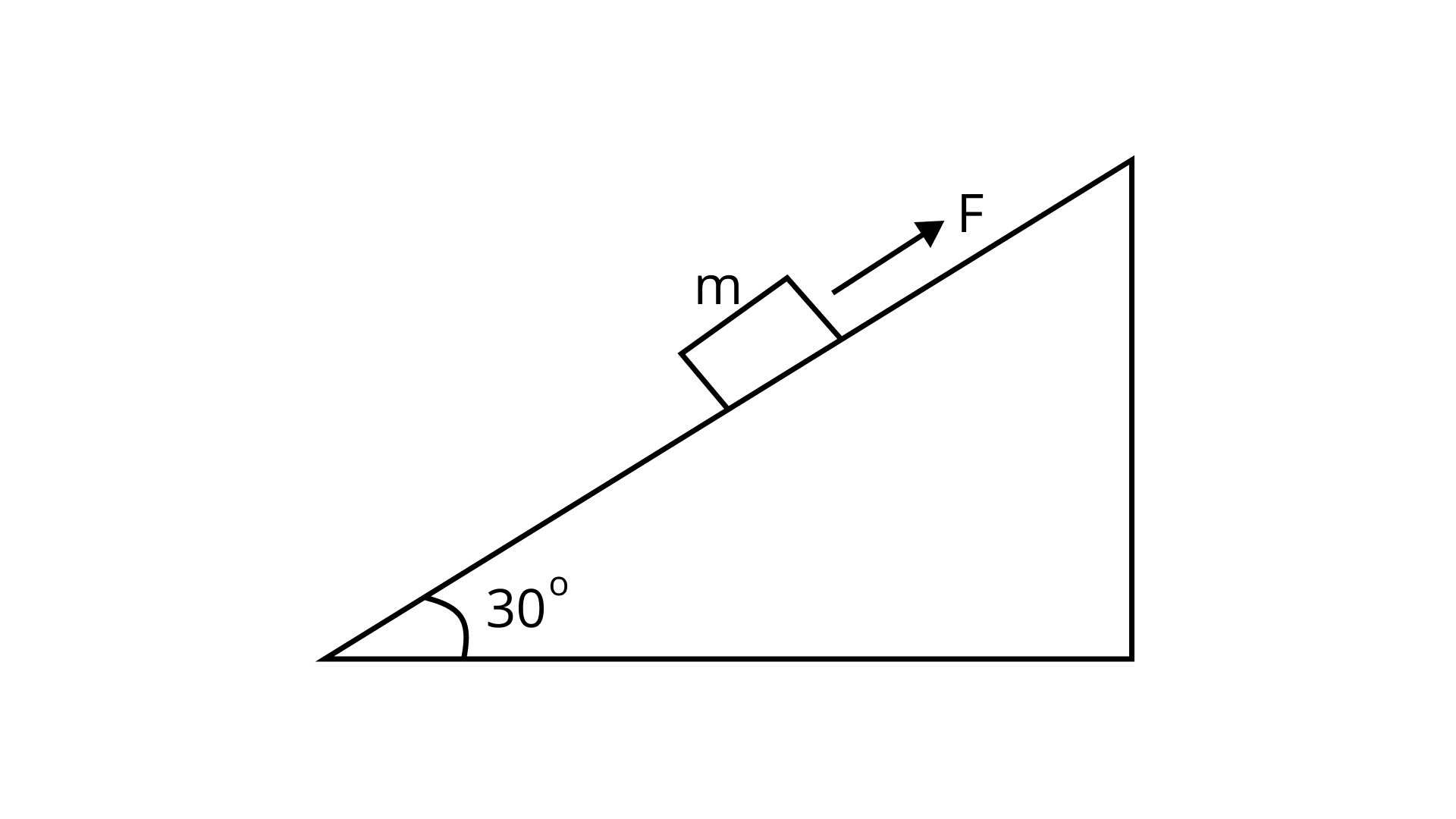
(a) work done against gravity

Ans: Work done in opposition to gravity $ = mgh$

$\sin {30^\circ } = \dfrac{h}{{10}}$

$h = 10\sin {30^\circ }$

$= 10 \times \dfrac{1}{2} = 5m.$ 

WD opposite to gravity $ = 1 \times 10 \times 5 = 50j$

(b) work done against force of friction

Ans:

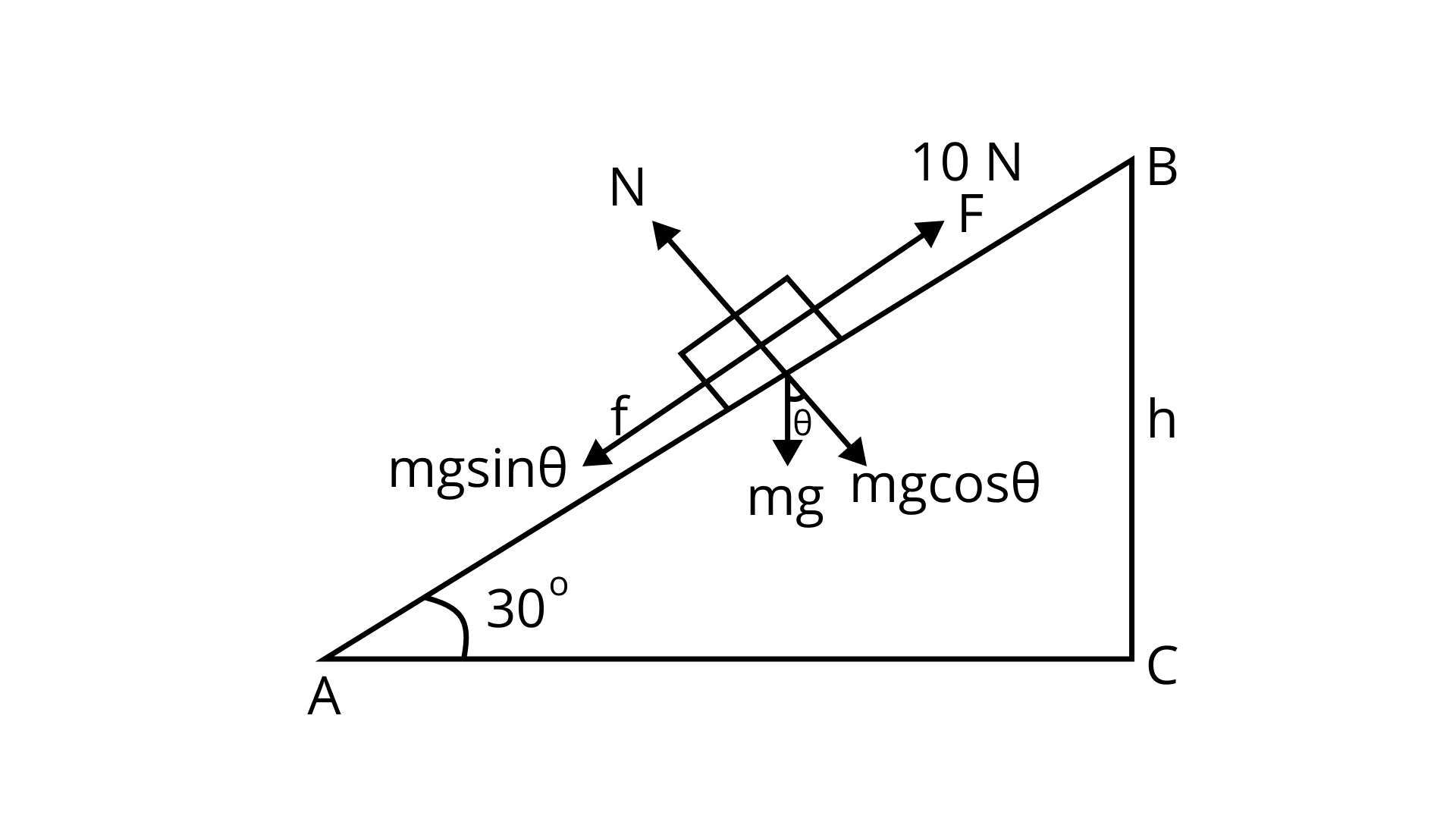
W.D opposite to frictional force,

$= \mu .mg\cos \theta$

$= 0.1 \times 1 \times 10\cos {30^\circ } \times 10$

$= 10 \times \frac{{\sqrt 3 }}{2} = 5\sqrt 3 j$ 

(c) increase in potential energy

Ans: Increase in potential energy= W.D opposite to gravite $ = 50J$

(d) increase in kinetic energy

Ans: $\Delta K = WD$

$\Delta K =  - mgh - fs + fs$

$=  - 50 - 5\sqrt 3  + 10 \times 10$

$= 50 - 5\sqrt 3 $

$= 5[10 - 1.732]$

$= 5[8.268]\Delta K$

$= 41.340{\text{J}}$ 

(e) work done by applied force.

Ans: $F \cdot s = 10 \times 10 = 100J$

6.45 A curved surface is shown in Fig. 6.16. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than C.

With the surface AB, ball $1$ has large enough friction to cause rolling down without slipping; ball $2$ has a small friction and ball $3$ has negligible friction.

(a) For which balls is total mechanical energy conserved?

Ans: Because the ball 1 is rolling down without slipping, there is no friction or loss of energy, and hence the whole mechanical energy is preserved.

Because Ball 3 has zero friction, there is no energy loss, and so total mechanical energy is preserved. As a result, mechanical energy is preserved for the ball 1 and 3.

(b) Which ball (s) can reach D?

Ans: Ball 1 gains rotational energy (due to friction);

ball 2 has little friction and hence loses energy through friction. 

As a result, it is unable to attain C. 

Ball 1 will slip owing to spin over a frictionless surface and so will not reach C.

(c) For balls which do not reach D, which of the balls can reach back A?

Ans: As mentioned in portion (b), balls 1 and 2 cannot reach C,

therefore ball 3 with minimal friction and A above C crosses C and may reach D

The energy in Ball 2 is depleted. 

Ball 3 crosses C, preventing any ball from reaching A.

6.46 A rocket accelerates straight up by ejecting gas downwards. In a small time interval$\Delta t$, it ejects a gas of mass $\Delta m$ at a relative speed u. Calculate ${\text{KE}}$ of the entire system at $t + \Delta t$ and t and show that the device that ejects gas does work $ = (1/2)\Delta m{u^2}$ in this time interval (neglect gravity).

Ans: At any point, you can release the rocket's mass$ = M$

Rocket velocity at any time$ = v$

${(KE)_{t + \Delta t}} = \frac{1}{2}(M - \Delta m){(v + \Delta v)^2} + \frac{1}{2}\Delta m{(v - u)^2}$

${(KE)_{t + \Delta t}} = \frac{1}{2}\left[ {(M - \Delta m)\left( {{v^2} + \Delta {v^2} + 2v\Delta v} \right) + \Delta m\left( {{v^2} + {u^2} - 2uv} \right)} \right]n$

${(KE)_{t + \Delta t}} = \frac{1}{2}$ 

${M{v^2} + M\Delta {v^2} + 2Mv\Delta v - \Delta m{v^2}}$ 

${ - \Delta m\Delta {v^2} - 2v\Delta m\Delta v + \Delta m{v^2} + }$ 

${\Delta m{u^2} - 2uv\Delta m}$ 

${(KE)_{t + \Delta t}} = \frac{1}{2}M{v^2} + Mv\Delta v + \frac{1}{2}\Delta m{u^2} - uv\Delta m$ 

Ignoring $\left. {[M\Delta {v^2},\Delta m\Delta {v^2},2v\Delta m\Delta v{\text{ }}\Delta {v^2}{\text{ , and }}\Delta m\Delta v} \right]$

${(KE)_t} = \frac{1}{2}M{v^2}n$

${(KE)_{t + \Delta t}} - {(KE)_t} = \frac{1}{2}M{v^2} + Mv\Delta v + \frac{1}{2}\Delta m{u^2} - uv\Delta m - \frac{1}{2}M{v^2}$

$\Delta K = \frac{1}{2}\Delta m{u^2} + v(M\Delta v - u\Delta m)$ 

Rocket reaction force (upward) = Action force by burned gases (downward)

$M\frac{{dv}}{{dt}} = \frac{{dm}}{{dt}}|u|(\because F = ma)$

$M\Delta v = \Delta mu \Rightarrow M\Delta v - u\Delta m = 0$ 

Putting Value in (i),

$K = \frac{1}{2}{u^2}\Delta m$

$\Delta (KE) = WD$

$W = \Delta K = \frac{1}{2}\Delta m{u^2}$

6.47 Two identical steel cubes (masses$50{\text{g}}$, side$1{\text{cm}}$) collide head-on face to face with a speed of $10{\text{cm}}/{\text{s}}$ each. Find the maximum compression of each. Young's modulus for steel$ = Y = 2 \times {10^{11}}{\text{N}}/{{\text{m}}^2}$.

Ans: A head-on collision occurs when two identical cubes contact. 

The KE of cubes is then converted into PE, and the faces of the cube are compressed by $\Delta$. 

According to Hooks' Law, stress $\alpha $ strain

$Y = \frac{{{\text{ stress }}}}{{{\text{ strain }}}}$

$\Rightarrow Y = \frac{{F \cdot L}}{{A\Delta L}}$

$F = AY\frac{{\Delta L}}{L}{\text{ }}$

$F = {L^2}Y\frac{{\Delta L}}{L} = LY\Delta L$ 

K.E. $ = 2\left( {\frac{1}{2}m{v^2}} \right) = 0.05 \times 0.1 \times 0.1 = 5 \times {10^{ - 4}}J$

W.D$ = $ K.E

$LY\Delta {L^2} = 5 \times {10^{ - 4}}\Delta {L^2}$

$= \frac{{5 \times {{10}^{ - 4}}}}{{0.01 \times 2 \times {{10}^{11}}}} = \frac{5}{2} \times {10^{ - 4 - 11 + 2}}$

$\Delta L = \sqrt {25 \times {{10}^{ - 14}}}  = 5 \times {10^{ - 7}}{\text{m}}$ 

6.48 A baloon filled with helium rises against gravity increasing its potential energy. The speed of the baloon also increases as it rises. How do you reconcile this with the law of conservation of mechanical energy? You can neglect viscous drag of air and assume that density of air is constant.

Ans: Because the pulling viscous force of the air on the balloon is ignored, there is 

Net Buoyant Force$ = Vpg$

Volume of air displaced $ \times $net density upward $ \times {\text{g}}$

$ = V\left( {{p_{ar}} - {p_{He}}} \right)g(upward)$

Let a be the upward acceleration on balloon then 

$ma = V\left( {{p_{ag}} - {p_{He}}} \right)g$

${\text{Where m}} = {\text{ mass of balloon }}$

${\text{V}} = {\text{ Volume of air displacement by balloon }} = {\text{ Volume of balloon }}$

${p_{{\text{air }}}} = {\text{ density of air }}$

${p_{He}} = {\text{ density of helium }}$

$m\frac{{dv}}{{dt}} = V \cdot \left( {{p_{ar}} - {P_{He}}} \right)g$ 

$mdv = V \cdot \left( {{p_{air}} - {p_{He}}} \right)g \cdot dt$

${\text{Integrating both sides }}mv = V \cdot \left( {{p_{ar}} - {p_{He}}} \right)gt$

$v = \frac{V}{m}\left( {{p_{air}} - {p_{He}}} \right)gt$

${\text{KE of balloon }} = \frac{1}{2}m{v^2}$

$\frac{1}{2}m{v^2} = \frac{1}{2}m\frac{{{V^2}}}{{{m^2}}}{\left( {{p_{air}} - {p_{He}}} \right)^2}{g^2}{t^2} = \frac{{{V^2}}}{{2m}}{\left( {{p_{air}} - {p_{He}}} \right)^2}{g^2}{t^2}\quad  \ldots ({\text{ ii }})$ 

If the balloon rises to a height h, from (i)

$a = \frac{V}{m}\left( {{p_{ai}} - {p_{he}}} \right)g$

$h = ut + \frac{1}{2}a{t^2} = 0.t + \frac{1}{2}\left[ {\frac{V}{m}\left( {{p_{ai}} - {p_{Bb}}} \right)g} \right]{t^2}$

$\therefore h = \frac{V}{{2m}}\left( {{p_{ar}} - {p_{He}}} \right)g{t^2}$ 

Rearranging the words of (ii) according to h in (ii) and (iii) (iii)

$\frac{1}{2}m{v^2} = \left\{ {\frac{V}{{2m}}\left( {{p_{air}} - {p_{He}}} \right)g{t^2}} \right\} \cdot V\left( {{p_{air}} - {p_{He}}} \right)g$

$\frac{1}{2}m{v^2} = \{ h\}  \cdot V\left( {{p_{air}} - {p_{He}}} \right)g$

$\frac{1}{2}m{v^2} = V \cdot \left( {{p_{at}} - {p_{He}}} \right)gh$

$\frac{1}{2}m{v^2} = V{p_{air}}gh - V{p_{H = }}gh$

$\frac{1}{2}m{v^2} + {p_{He}}Vgh = {p_{av}}Vgh$

$K{E_{ballon}} + P{E_{ballon}} = {\text{ Change in PE of air}}{\text{. }}$ 

As a result, as the balloon rises, an equivalent volume of air falls, increasing the balloon's PE and KE at the expense of the air's PE (which comes down).

Chapter Description

‘Work,’ ‘Energy,’ and ‘Power’ are very common words used in our day to day life. Each and every physical or mechanical change in our environment can be quantified by these principles. The sixth chapter of NCERT class 11 Physics book tells us about the dissipation or transformation of different forms of energy that we use to get work done.  The scalar or dot product of two or more vectors is the foundation of this chapter as described in the introductory section 6.1.  The study of the ‘Work Energy Theorem’ begins with section 6.2 ‘Notions of Work and Kinetic Energy. This section introduces us to work as done by the force on a body going through a displacement. Section 6.3 ‘Work’ defines work in terms of force and displacement. ‘Kinetic Energy’ is another aspect of a body in motion and has been defined in section 6.4. But as we all know it is very difficult to impose constant force on any object so we have to measure the resultant force with respect to time in section 6.5 ‘Work Done by a Variable Force’ and its theorem in section 6.6.

A body in rest is also as intriguing as a body in motion. It possesses energy due to position, orientation and structures described in section 6.7 ‘The Concept of Potential Energy.’ Section 6.8 ‘The Conservation of  Mechanical Energy’ describes the conservation of various forces acting on a body in rest. Spring is such an excellent object which can store energy to a certain limit when forces act upon it. Thus section 6.9 ‘The Potential Energy of a Spring’ describes the spring force as a conservative force. 

After learning  the two types of mechanical energy, ‘Kinetic Energy’ and ‘Potential Energy’ the description about various other forms of energy begins in section  6.10 ‘The Law of Conservation of Energy.’ It includes the concepts of ‘Heat Energy,’ ‘Chemical Energy,’ ‘Electrical Energy,’ ‘Nuclear Energy,’ and ‘The Equivalent of Mass and Energy.’ 

Section 6.11 ‘Power’ defines it as the time rate at which energy is transferred or work is done. ‘Collisions’ are another interesting phenomenon studied in mechanical physics. This has been covered in the last section 6.12. sub-sections include ‘Elastic and Inelastic Collisions,’ ‘Collisions in One Dimension,’ and ‘Collisions in Two Dimensions.’

Once you complete studying the full chapter every student must by heart the symbolic representation of terms and their equations. The exercise following the chapter theory contains all types of questions required for an all-around understanding of the subject. You can solve the questions by yourself or can refer to the solutions provided by experts on the Vedantu website for reference.