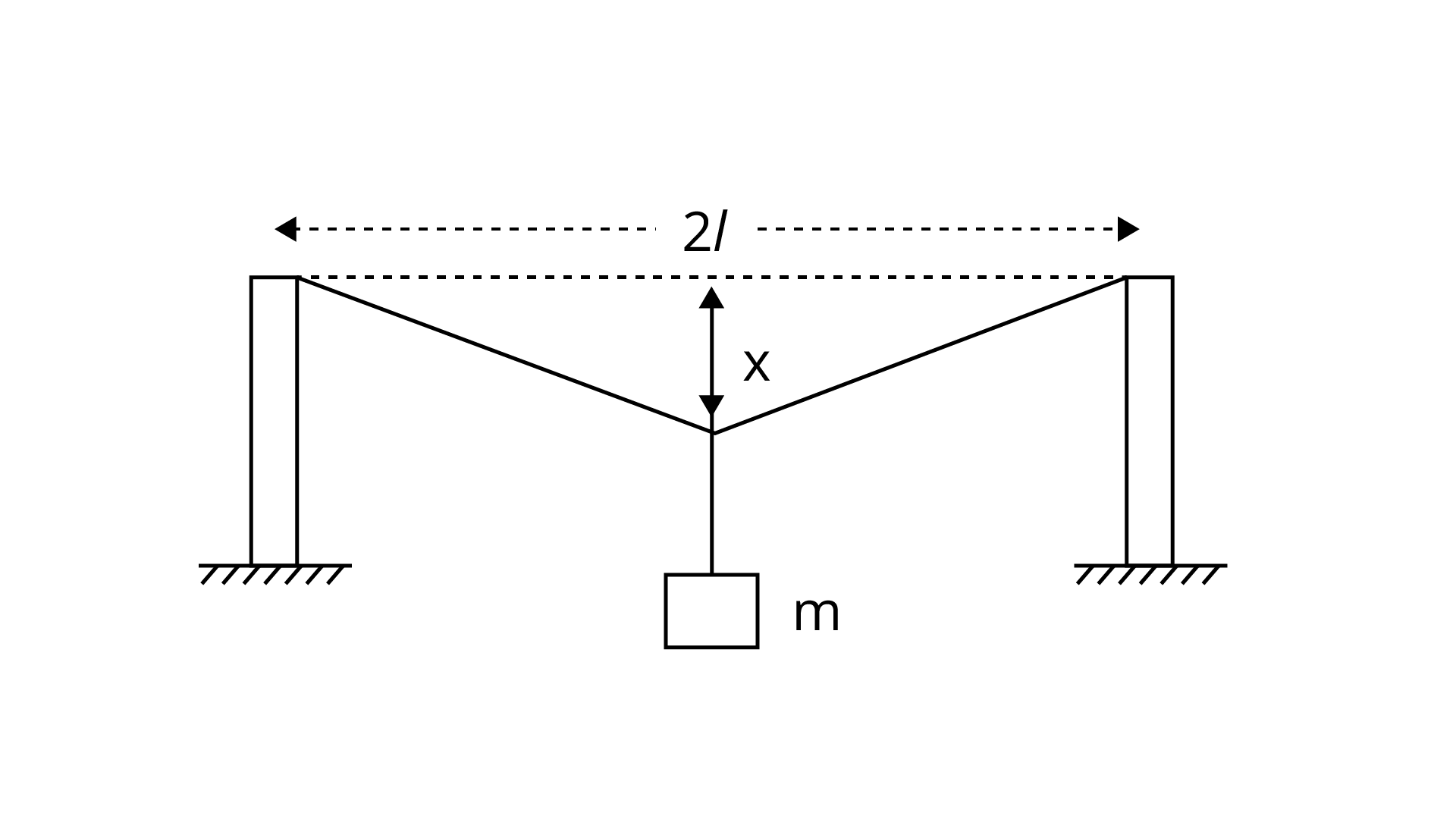
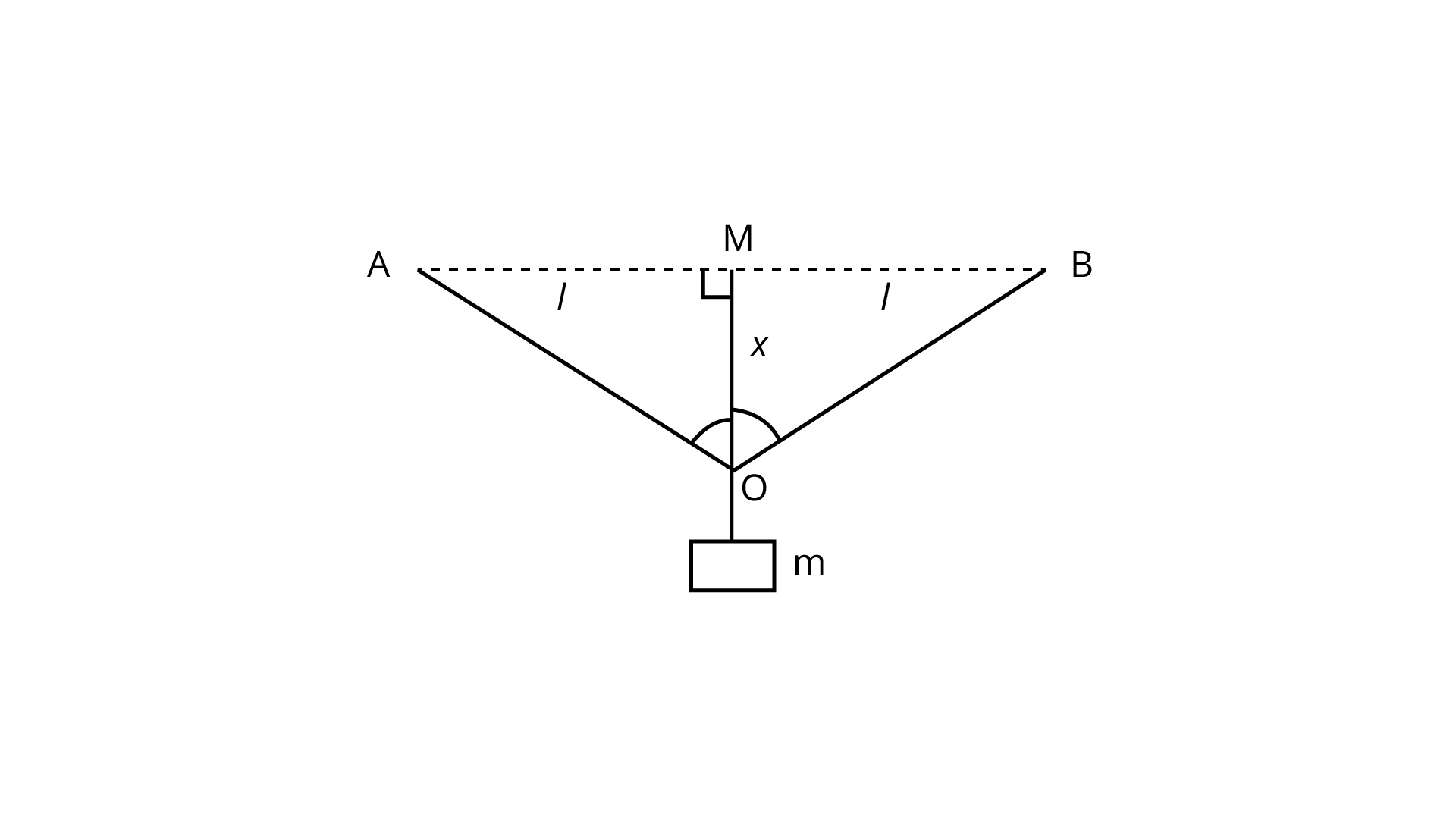
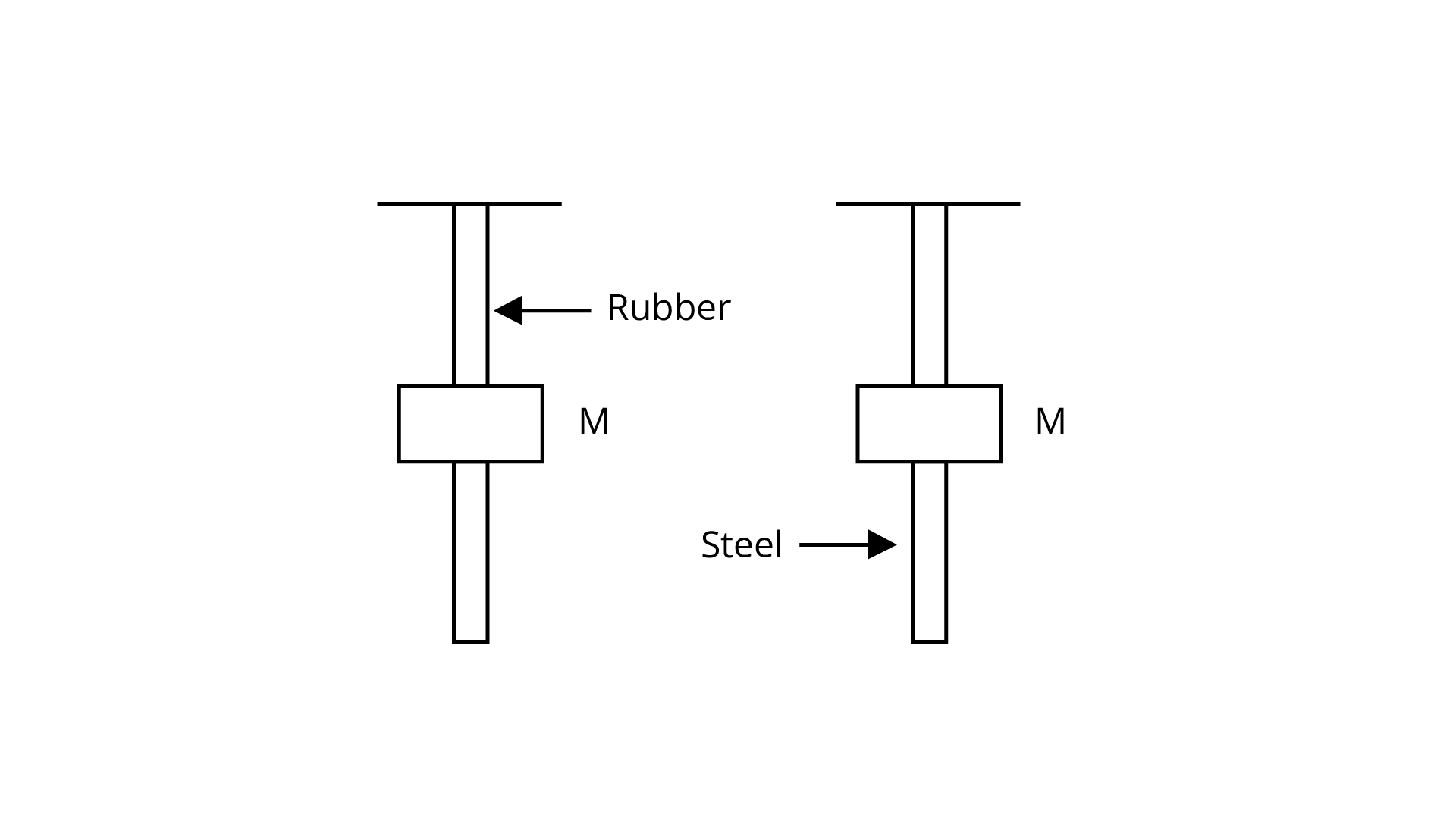
NCERT Exemplar for Class 11 Physics - Mechanical Properties of Solids - Free PDF Download
FAQs on NCERT Exemplar for Class 11 Physics Chapter 9 - Mechanical Properties of Solids (Book Solutions)
1. What are the different Mechanical properties of a particular matter?
The Mechanical properties of particulate matter suggest the various properties of a matter that define the various states of the matter. The concept of the properties of matters has been introduced by CBSE in the syllabus of the students who are preparing for Class 11 and who have opted for Physics as a subject. By studying the Chapters involving the definitions and descriptions of the properties of matter, the students will get to learn about the Elasticity, Stress, Plasticity, and Strain of various matters. Students will learn about various laws that will help them to analyze the concept further.
2. What is suggested by Hooke's law?
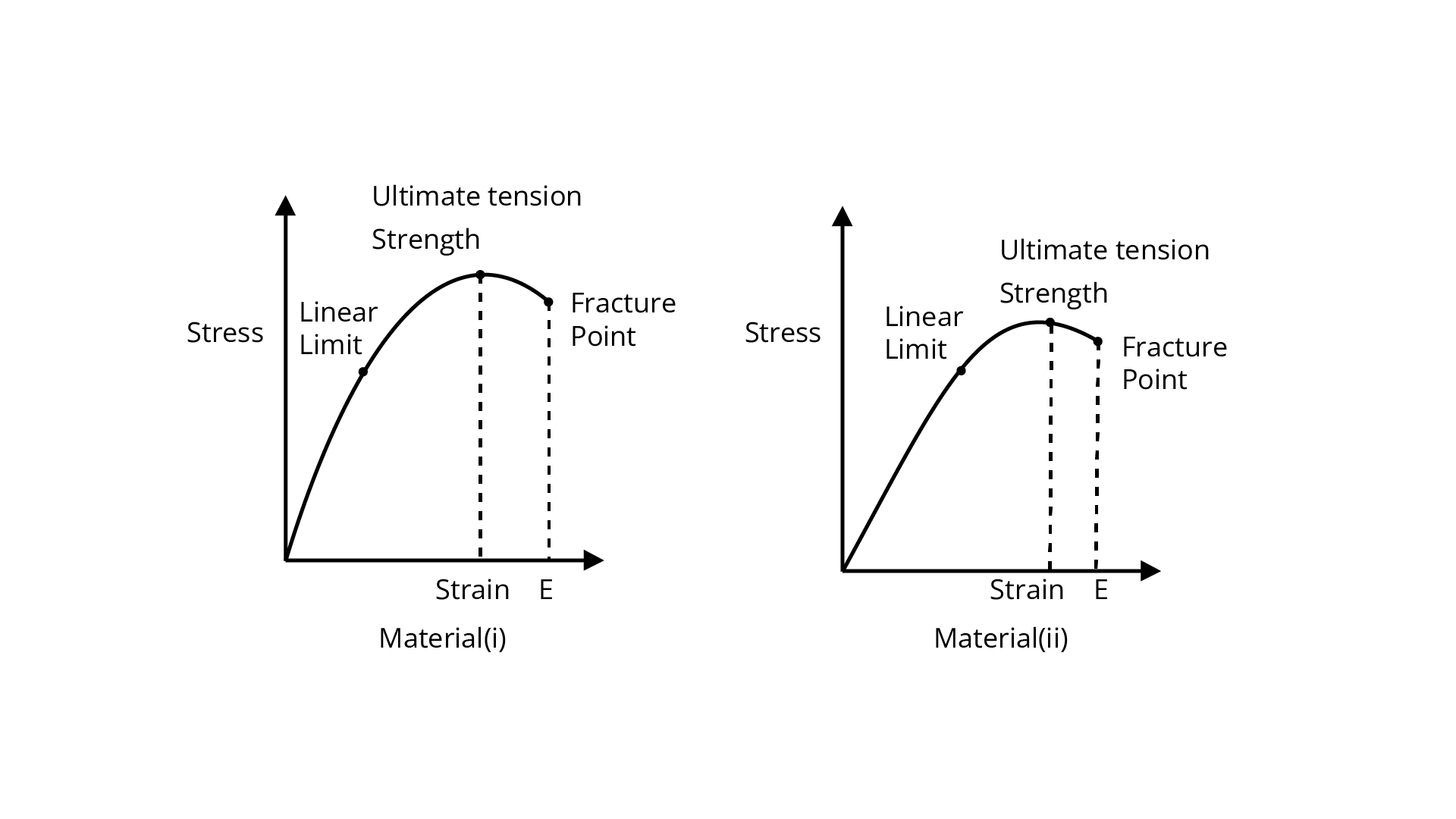
This particular law establishes a proven relationship between the stress and strain produced in a particular matter. The law and equation show the direct relationship between the stress and strain considering the constant elastic limit. If the elastic limit is considered to be constant then there can be a direct relationship between the stress and strain which will be directly proportional to each other. In short, if we increase the strain, the stress will also be increased and if we decrease the strain, the stress will also be decreased considering the same elastic limit.
3. Is studying the concept of Mechanical properties important to score well in JEE Main and Advanced?
To qualify for JEE Main or Advanced and to score well in any other Engineering entrance Examination, it is very important for the students that they cover all the topics that have been included in their CBSE syllabus and they go through all the Chapters that are there in the NCERT books. One of the important topics that they have to cover before they appear for the Examinations is the Mechanical properties of different types of matters. It is one of the basic and fundamental concepts of Physics that they need to understand if they want to continue their studies in Physics.
4. What are the study materials that the students should consult to understand the concept of Mechanical properties of Solids?
The NCERT books prescribed by the CBSE are the best study materials that the students can consult. The NCERT Exemplars designed for the Class 11 students can provide them with the detailed guideline of how they should study and what are the important questions that they should consider solving to score well in the Examinations. NCERT Exemplar provides the students with the detailed syllabus that they have to cover and they will get a good idea of all the Chapters from which questions can be there in their Examination.
5. What are the websites to download free study materials for Class 11?
All the important course materials and solved question papers are available on the website of Vedantu. The NCERT Exemplar that is meant for the Class 11 students is available for free on the website and the students can download them in PDF format. Various revision notes and sample question paper sets can help them to get prepared for the Examinations in the most effective and organized way. The questions are solved by learned and experienced trainers who have specialized in their own fields. Also, taking the help of the important notes is highly important for the students because they do not get a lot of time to cover all the Chapters unless they follow a strategic method to study.