Question

An athlete runs on a circular track, whose radius is 50 m with a constant speed. It takes 50 second to reach a diametrically opposite point B from starting point A. Find:
(a) Distance covered
(b) Displacement and
(c) Speed.

Answer 1

Hint: i) Moving between point A and B, the athlete covered half of the circumference of the circular track which would determine the distance covered by him.
ii) In case of circle, diameter is possible shortest path travelled between diametrically opposite points.
Formula used
\[2\pi r\]= circumference of circular track
\[ \Rightarrow speed = \dfrac{distance\ covered}{time\ taken}\]

Complete Step by Step solution
Given, Athletes run with a constant speed. That means, he covers the same distance at the same time. For instance, if he covers 3 meters in 10 seconds then in another 10 seconds he covered 3 meters again.


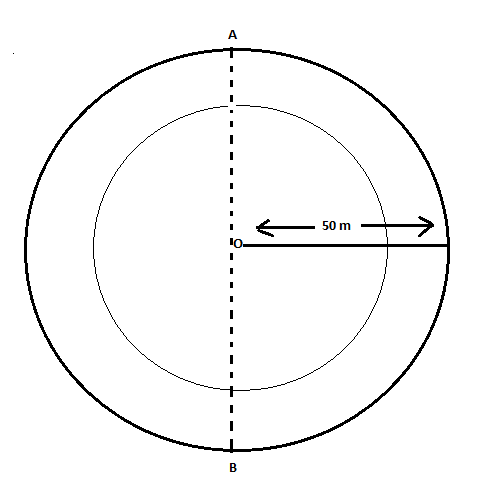
To find distance covered by him while running on a circular track from point A to B.
So, the distance covered by him in 50 second = \[\dfrac{{track circumference}}{2}\] because, distance covered will become equal to half the circumference of the circle.
Also, given that, radius of circular track = 50 m
\[ \Rightarrow dis\tan ce\operatorname{cov} ered = \dfrac{{2\pi r}}{2}\]…………………………………..eq.1
Where \[2\pi r\]= circumference of circular track
And r = radius of track
It’s clear from figure, that radius of circular track = 50 m, so circumference is given by:
\[ \Rightarrow 2\pi r = 2 \times 3.14 \times 50\]
\[ \Rightarrow 2\pi r = 314.15\]……………………………………eq.2
Substituting values from eq.2 in eq.1, we get,
\[
   \Rightarrow dis\tan ce\ operatorname{cov} ered = \dfrac{{314.15}}{2} \\
   \Rightarrow dis\tan ce\ operatorname{cov} ered = 157.08meter \\
 \]
\[\therefore \] The total distance covered by an athlete to reach a diametrically opposite point B from starting point A is 157.08 meter.

(B) To find displacement :
Now, displacement of a particle is the change in the position of a particle in a particular direction.
Or in simple words, it is the shortest path that should be covered by an object between two fixed points.
See in below given figure, the shortest path between points A and B is shown as:

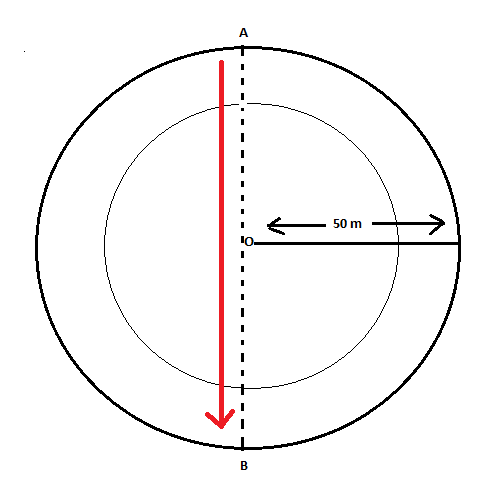
So, moving on a straight path from A to B gives us displacement between these points and this path is the diameter of a circular running track.
\[ \Rightarrow \] Displacement = diameter of circular track
\[ \Rightarrow displacement = 2 \times radius\]
\[
   \Rightarrow displacement = 2 \times 50 \\
   \Rightarrow displacement = 100meter \\
 \]
Since, displacement is a vector quantity and hence always associated with a particular direction. So, the direction of displacement would be from A to B.
Therefore, displacement between point A and B is of magnitude 100 meter with a direction from A to B.
(C) To find the speed of athlete:
Since, in kinematics we all have studied the time rate of change of position of an object is called speed. Or, the ratio of total distance covered to total time covered.
\[ \Rightarrow speed = \dfrac{{dis\tan ce\operatorname{cov} ered}}{{time\ taken}}\]
\[ \Rightarrow speed = \dfrac{{track\ circumference}}{2} \times \dfrac{1}{{time\ taken}}\]
\[ \Rightarrow speed = \dfrac{{2\pi r}}{2} \times \dfrac{1}{{time\ taken}}\]
It takes 50 second to reach a diametrically opposite point B from starting point A.
\[ \Rightarrow \]Time taken = 50 seconds …………………eq.3
\[\therefore \]Substituting the values from eq.1, eq.2 and eq.3 we get,
\[ \Rightarrow speed = \dfrac{{314.15}}{2} \times \dfrac{1}{{50}}\]
\[ \Rightarrow speed = \dfrac{{314.15}}{{100}}\]
\[ \Rightarrow speed = 3.1415\]meter /sec or,
\[ \Rightarrow speed = 3.1415\]m /sec or,
\[ \Rightarrow speed = 3.1415m{s^{ - 1}}\]

Note It should be noted that the actual distance travelled by an object is either equal or greater than magnitude of displacement because displacement is the shortest path covered by object. Also, we above calculated that distance = 157.08 meter and displacement = 100 meter. And always displacement is associated with direction, so determine direction always along with magnitude of displacement and velocity.