NCERT Solutions for Class 12 Maths Chapter 10 - In Hindi

प्रश्नावली 10.1

1. उतर से ${{30}}^\circ$ पूर्व मे ${{40 km}}$ के विस्थापन का आलेखीय निरूपण कीजिए। 

उत्तर: 

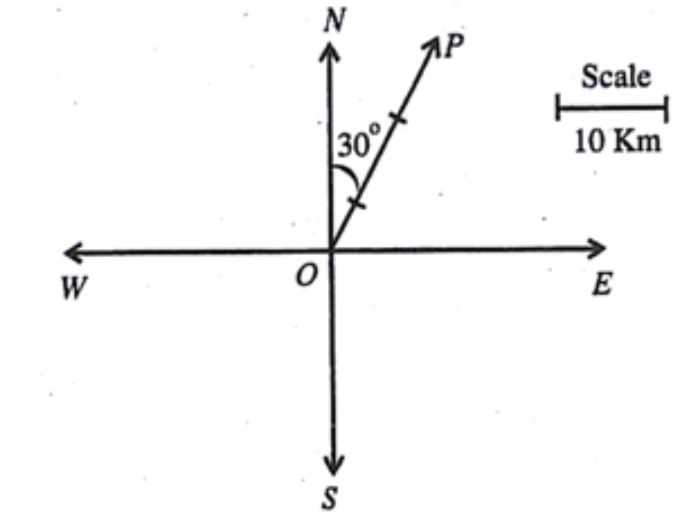
सदिश OP अभीष्ट विस्थापन को निरूपित करता है। 

2. निम्नलिखित मापों को अदिश एवं सदिश के रूप मे श्रेणीबद्ध कीजिए। 

उत्तर: (a) ${{10 kg}}$ - अदिश 

(b) ${{2 m}}$ उतर पश्चिम -  विस्थापन सदिश 

(c) ${{40}}^\circ$ - अदिश 

(d) $40$ वाट -  अदिश 

(e) ${{1}}{{{0}}^{{{ - 19}}}}$ कूलम्ब -  अदिश 

(f) ${{20 m/}}{{{s}}^{{2}}}$ -  सदिश 

3. निम्नलिखित को अदिश एवं सदिश के रूप मे श्रेणीबद्ध कीजिए। 

उत्तर: (a) समय कालांश – अदिश 

(b) दूरी – अदिश 

(c) बच – सदिश 

(d) वेग – सदिश 

(e) कार्य – अदिश 

4. 

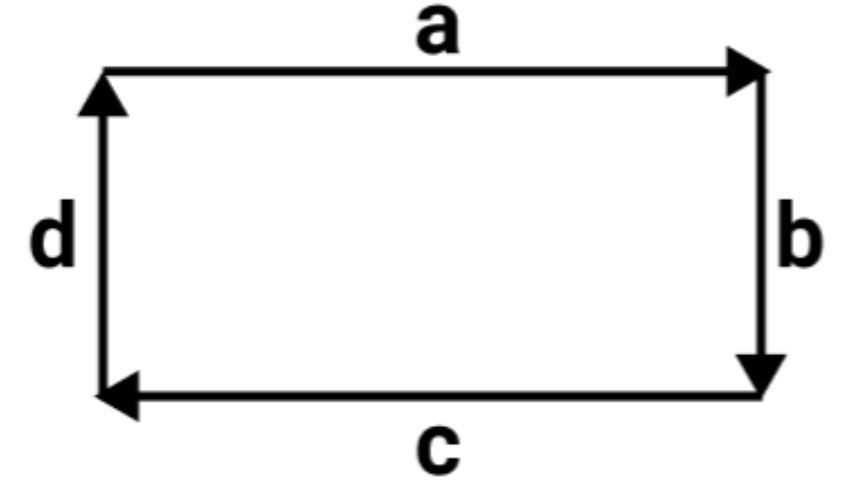
उत्तर: (i) सह – आदिम – d , a 

(ii) समान – d , b 

(iii) संरेख परंतु असमान – a , c 

5. निम्नलिखित का उत्तर सत्य अथवा असत्य के रूप मे दीजिए। 

(i) a तथा -a संरेख है। 

उत्तर: सत्य 

(ii) दो संरेख सदिशों का परिणाम सदैव समान होता है। 

उत्तर: असत्य 

(iii) समान परिणाम वाले दो सदिश संरेख होते है। 

उत्तर: असत्य 

(iv) समान परिणाम वाले दो सदिश समान होते है। 

उत्तर:  असत्य 

प्रश्नावली 10.2 

1. निम्नलिखित सदिशों के परिमाण का परिकलन कीजिए:

${{a  =  i + j + k ; b  =  2i - 7j - 3k ; c  =  13i + 13j - 13k}}$

उत्तर: ${{a  =  i + j + k ; b  =  2i - 7j - 3k ; c  =  13i + 13j - 13k}}$

${{|a|  =  }}\sqrt {{{{{(1)}}}^{{2}}}{{ + (1}}{{{)}}^{{2}}}{{ + (1}}{{{)}}^{{2}}}} {{  =  }}\sqrt {{3}}$

${{|b|  =  }}\sqrt {{{{{(2)}}}^{{2}}}{{ + ( - 7}}{{{)}}^{{2}}}{{ + ( - 3}}{{{)}}^{{2}}}} {{  =  }}\sqrt {{{4 + 49 + 9}}} {{  =  }}\sqrt {{{62}}}$

${{|c|  =  }}\sqrt {{{\left( {\dfrac{{{1}}}{{\sqrt {{3}} }}} \right)}^{{2}}}{{ + }}{{\left( {\dfrac{{{1}}}{{\sqrt {{3}} }}} \right)}^{{2}}}{{ + }}{{\left( {{{ - }}\dfrac{{{1}}}{{\sqrt {{3}} }}} \right)}^{{2}}}} {{  =  }}\sqrt {\dfrac{{{1}}}{{{3}}}{{ + }}\dfrac{{{1}}}{{{3}}}{{ + }}\dfrac{{{1}}}{{{3}}}} {{  =  1}}$ 

2. समान परिमाण वाले दो विभित्र सदिश लिखिए।

उत्तर: मान लीजिए विभिन्न दो सदिश ${{a  =  i + 2j + k, b  =  i + j + 2 k}}$

a का परिणाम = $\left| {{a}} \right|\;{{ = }}\;\sqrt {{{{1}}^{{2}}}{{ + }}{{{2}}^{{2}}}{{ + }}{{{1}}^{{2}}}} \;{{ = }}\;\sqrt {{6}}$

b का परिणाम = $\left| {{b}} \right|\;{{ = }}\;\sqrt {{{{1}}^{{2}}}{{ + }}{{{1}}^{{2}}}{{ + }}{{{2}}^{{2}}}} \;{{ = }}\;\sqrt {{6}}$

इस प्रकार a  और b दो सदिश है जिनके परिणाम समान है। (ऐसे अनंत सदिश हो सकते है)

3. समान दिशा वाले दो विभित्न सदिश लिखिए।

उत्तर: मान लीजिए विभिन्न दो सदिश ${{a}  =  (\hat i + }\widehat {{j}}{{ + }}\widehat {{k}}{{), b  =  (2}}\widehat {{i}}{{ + 2j + 2}}\widehat {{k}}{{)}}$

a के cosine

${{l  =  }}\dfrac{{{1}}}{{\sqrt {{{{1}}^{{2}}}{{ + }}{{{1}}^{{2}}}{{ + }}{{{1}}^{{2}}}} }}{{  =  }}\dfrac{{{1}}}{{\sqrt {{3}} }}{{, m  =  }}\dfrac{{{1}}}{{\sqrt {{{{1}}^{{2}}}{{ + }}{{{1}}^{{2}}}{{ + }}{{{1}}^{{2}}}} }}{{  =  }}\dfrac{{{1}}}{{\sqrt {{3}} }}{{, n  =  }}\dfrac{{{1}}}{{\sqrt {{{{1}}^{{2}}}{{ + }}{{{1}}^{{2}}}{{ + }}{{{1}}^{{2}}}} }}{{  =  }}\dfrac{{{1}}}{{\sqrt {{3}} }}$

a के दिक कोसाइन = $(\dfrac{{{1}}}{{\sqrt {{3}} }}{{, }}\dfrac{{{1}}}{{\sqrt {{3}} }}{{, }}\dfrac{{{1}}}{{\sqrt {{3}} }})$

b  के cosine${{l  =  }}\dfrac{{{2}}}{{\sqrt {{{{2}}^{{2}}}{{ + }}{{{2}}^{{2}}}{{ + }}{{{2}}^{{2}}}} }}{{  =  }}\dfrac{{{2}}}{{{{2}}\sqrt {{3}} }}{{  =  }}\dfrac{{{1}}}{{\sqrt {{3}} }}{{, m  =  }}\dfrac{{{2}}}{{\sqrt {{{{2}}^{{2}}}{{ + }}{{{2}}^{{2}}}{{ + }}{{{2}}^{{2}}}} }}{{  =  }}\dfrac{{{2}}}{{{{2}}\sqrt {{3}} }}{{  =  }}\dfrac{{{1}}}{{\sqrt {{3}} }}{{, n  =  }}\dfrac{{{2}}}{{\sqrt {{{{2}}^{{2}}}{{ + }}{{{2}}^{{2}}}{{ + }}{{{2}}^{{2}}}} }}{{  =  }}\dfrac{{{2}}}{{{{2}}\sqrt {{3}} }}{{  =  }}\dfrac{{{1}}}{{\sqrt {{3}} }}$

b के दिक कोसाइन = $(\dfrac{{{1}}}{{\sqrt {{3}} }}{{, }}\dfrac{{{1}}}{{\sqrt {{3}} }}{{, }}\dfrac{{{1}}}{{\sqrt {{3}} }})$

इस प्रकार a, b एक ही दिशा मे है। 

4. ${{x, y}}$  के मान ज्ञात कीजिए ताकि सदिश ${{2j + 3k}}$ और ${{xi + yj}}$  समान हों।

उत्तर: माना ${{a  =  2j + 3k,  b  =  xi + yj}}$ दिए गए सदिश है। 

a, b  के गुणांकों की तुलना करने पर ${{x  =  2, y  =  3}}$

5. एक सदिश का प्रारंभिक बिंदु ${{(2,1)}}$ है और अंतिम बिंदु ${{( - 5,7)}}$ है। इस सादिश के अदिश एवं सदीश घटक ज्ञात कीजिए।

उत्तर: माना सदिश के प्रारम्भिक वे अन्तिम बिन्दु क्रमशः $A(2,1), B(-5,7)$ हें।

$\therefore \overrightarrow{A B}=\left(x_{2}-x_{1}\right) \hat{i}+\left(y_{2}-y_{1}\right) \hat{j}$

$=(-5-2) \hat{i}+(7-1) \hat{j}$

$=-7 \hat{i}+6 \hat{j}$

$\therefore$ दिए गए अदिश घटक $-7$ और 6 है; जबकि सदिश घटक $-7 \hat{i}$ और $6 \hat{j}$ हैं।

6. सादिश ${{a  =  i - 2j + k, b  =   - 2i + 4j + 5k, c  =  i - 6j - 7k}}$  का योगफल ज्ञात कीजिए।

उतर: ${{a  =  i - 2j + k, b  =   - 2i + 4j + 5k, c  =  i - 6j - 7k}}$

योगफल ${a + b + c}=(1 - 2 + 1)\hat i + ( - 2 + 4 - 6)\hat j + (1 + 5 - 7)\hat k$

${{ =  0}}\hat i - 4\hat j - 1 \times \hat k$

$= - 4\hat j - \hat k$ 

7. सदिशा ${{a  =  i + j + 2k}}$  के अनुदिश एक मात्रक सादिश ज्ञात कीजिए।

उत्तर: ${{a  =  i + j + 2k}}$

$\vec{a}=\hat{i}+\hat{j}+2 k$

$\therefore|\vec{a}|=\sqrt{1^{2}+1^{2}+2^{2}}=\sqrt{6}$

Unit vector in the direction of vector a

$\hat{\mathrm{a}} =\dfrac{\overrightarrow{\mathrm{a}}}{|\overrightarrow{\mathrm{a}}|}=\dfrac{1}{\sqrt{6}}(\hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}})$

$=\dfrac{1}{\sqrt{6}} \hat{\mathrm{i}}+\dfrac{1}{\sqrt{6}} \hat{\mathrm{j}}+\dfrac{2}{\sqrt{6}} \hat{\mathrm{k}}$

8. सादिशा ${{PQ}}$  के अनुदिश मात्रक सदिश ज्ञात कीजिए जहाँ बिंदु ${{P, Q}}$  क्रमशः ${{(1,2,3), (4,5,6)}}$  है।

उत्तर: बिन्दु ${{P, Q}}$  क्रमशः ${{(1,2,3), (4,5,6)}}$ को मिलाने वाला सदिश 

$\overrightarrow{\mathrm{PQ}}=(4-1) \hat{\mathrm{i}}+(5-2) \hat{\mathrm{j}}+(6-3) \hat{\mathrm{k}}=3 \mathrm{i}+3 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}$

$|\overrightarrow{\mathrm{PQ}}|=\sqrt{3^{2}+3^{2}+3^{2}}=\sqrt{9+9+9}=\sqrt{27}=3 \sqrt{3}$

मात्रक सदिश $\mathrm{PQ}$ जो $\mathrm{PQ}$ के अनुदिश है।

$\dfrac{\overrightarrow{\mathrm{PQ}}}{|\overrightarrow{\mathrm{PQ}}|}=\dfrac{3 \mathrm{i}+3 \hat{\mathrm{j}}+3 \mathrm{k}}{3 \sqrt{3}}=\dfrac{1}{\sqrt{3}} \mathrm{i}+\dfrac{1}{\sqrt{3}} \mathrm{j}+\dfrac{1}{\sqrt{3}} \mathrm{k}$

9. दिए हुए सादिशों ${{a  =  2i - j + 2k, b  =   - i + j - k}}$  के लिए ${{a + b}}$  सदिश ज्ञात कीजिए।

उत्तर: दिए हुए सदिश ${{a  =  2i - j + 2k, b  =   - i + j - k}}$

$a+b=(2-1) \hat{i}+(-1+1) \hat{j}+(2-1) \hat{k}=1 \hat{i}+0 \hat{j}+1 \hat{k}=i+\hat{k}$

$|a+b|=\sqrt{1^{2}+1^{2}}=\sqrt{2}$

$\dfrac{(a+b)}{|a+b|}=\dfrac{\hat{i}+\hat{k}}{\sqrt{2}}=\dfrac{1}{\sqrt{2}} \hat{i}+\dfrac{1}{\sqrt{2}} \hat{k}$

10. सदिश ${{5i - j + 2k}}$  के अनुदिशएक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण ${{8}}$ इकाई है।

उत्तर: माना $\mathrm{a}=5 \hat{\mathrm{i}} \hat{\mathrm{j}}+2 \hat{\mathrm{k}}$

a का परिणाम 

$|\vec{a}|=\sqrt{5^{2}+(-1)^{2}+2^{2}}=\sqrt{25+1+4}=\sqrt{30}$

a के अनुदिश मात्रक सदिश 

$\mathrm{a}=\dfrac{\mathrm{a}}{|\mathrm{a}|}=\dfrac{5 \hat{\mathrm{i}}- \hat{\mathrm{j}}+2 \hat{\mathrm{k}}}{\sqrt{30}}$

a के अनुदिश आठ इकाई वाला सदिश 

$8 \mathrm{a}=8\left(\dfrac{5 \hat{\mathrm{i}}- \hat{\mathrm{j}}+2 \hat{\mathrm{k}}}{\sqrt{30}}\right)=\dfrac{40}{\sqrt{30}} \hat{\mathrm{i}}-\dfrac{8}{\sqrt{30}} \hat{\mathrm{j}}+\dfrac{16}{\sqrt{30}} \hat{\mathrm{k}}$

11. दशर्शाइए की सदिश $2 \mathrm{i}-3 \mathrm{j}+4 \mathrm{k},-4 \mathrm{i}+6 \mathrm{j}-8 \mathrm{k}$ संरेख है।

उत्तर: माना $a=2 \hat{i}-3 \hat{j}+4 \hat{k}, b=-4 \hat{i}+6 \hat{j}-8 \hat{k}$

$\mathrm{b}=-4 \hat{\mathrm{i}}+6 \hat{\mathrm{j}}-8 \hat{\mathrm{k}}=-2(2 \hat{\mathrm{i}}-3 \hat{\mathrm{j}}+4 \hat{\mathrm{k}})-2 \mathrm{a}$

$\therefore \mathrm{b}=\lambda \mathrm{a}$ जहा $\lambda=-2$

अतः $a, b$ संरेख है।

12. सदिश $i+2 j+3 k$ की दिक cosine ज्ञात कीजिए।

उत्तर: माना $a=\hat{i}+2 \hat{j}+3 \hat{k}$

a के cosine $=|\vec{a}|=\sqrt{1^{2}+2^{2}+3^{2}}=\sqrt{1+4+9}=\sqrt{14}$

$a$ के दिक cosine $=\left(\dfrac{1}{\sqrt{14}}, \dfrac{2}{\sqrt{14}}, \dfrac{3}{\sqrt{14}}\right)$

13. बिंदुओं $\mathrm{A}(1,2,-3), \mathrm{B}(-1,-2,1)$ को मिलने वाले एवं $\mathrm{A}$ से $\mathrm{B}$ की तरफ़ दिष्ट सदिश की दिक् cosine ज्ञात कीजिए।

उत्तर: बिन्दु $\mathrm{A}(1,2,-3), \mathrm{B}(-1,-2,1)$ को मिलने वाले सदिश

$\overrightarrow{\mathrm{AB}}=(-1-1) \hat{\mathrm{i}}+(-2-2) \hat{\mathrm{j}}+(1-(-3)) \hat{\mathrm{k}}$ $\overrightarrow{\mathrm{AB}}=-2 \hat{\mathrm{i}}-4 \hat{\mathrm{j}}+4 \hat{\mathrm{k}}$ $|\overrightarrow{\mathrm{AB}}|=\sqrt{(-2)^{2}+(-4)^{2}+4^{2}}=\sqrt{4+16+16}=\sqrt{36}=6$ 

$\mathrm{AB}$ की दिक कोसाइन $=\left(-\dfrac{2}{6},-\dfrac{4}{6}, \dfrac{4}{6}\right)=\left(-\dfrac{1}{3},-\dfrac{2}{3}, \dfrac{2}{3}\right)$

14. दर्शाइए कि सदिश $\mathrm{i}+\mathrm{j}+\mathrm{k}$ अक्षों $ \mathrm{OX}, \mathrm{OY}, \mathrm{OZ}$ के साथ बराबर झुका हुआ है।

उत्तर: माना $a=i+j+k$

$|\mathrm{a}|=\sqrt{1^{2}+1^{2}+1^{2}}=\sqrt{3}$

a की दिक कोसाइन $=\left(\dfrac{1}{\sqrt{3}}, \dfrac{1}{\sqrt{3}}, \dfrac{1}{\sqrt{3}}\right)$

दिक कोसाइन समान होने के कारण सदिश अक्षों $\mathrm{OX}, \mathrm{OY}, \mathrm{OZ}$ के साथ बराबर झुका हुआ है।

15. बिन्दुओ $\mathrm{P}(\mathrm{i}+2 \mathrm{j}-\mathrm{k}), \mathrm{Q}(-\mathrm{i}+\mathrm{j}+\mathrm{k})$ को मिलाने वाली रेखा को $2: 1$ के अनुपात में

(i) अते:

उत्तर: बिन्दु $\mathrm{OP}(\mathrm{i}+2 \mathrm{j}-\mathrm{k}), \mathrm{OQ}(-\mathrm{i}+\mathrm{j}+\mathrm{k})$ को अंत: $\mathrm{m}: \mathrm{n}$ अनुपद मे विभाजित करने वाला बिन्दु $\mathrm{R}$ का स्थित सदिश

$\overrightarrow{\mathrm{OR}}=\dfrac{2(-\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})+1(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}})}{2+1}=\dfrac{(-2 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+2 \hat{\mathrm{k}})+(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}})}{3}$

$=\dfrac{-\hat{\mathrm{i}}+4 \hat{\mathrm{j}}+\hat{\mathrm{k}}}{3}=-\dfrac{1}{3} \hat{\mathrm{i}}+\dfrac{4}{3} \hat{\mathrm{j}}+\dfrac{1}{3} \hat{\mathrm{k}}$

(ii) बाह्य, विभाजित करने वाले बिदुदु $R$ का स्थिति सदिश ज्ञात कीजिए।

उत्तर: बिन्दु $\mathrm{OP}(\mathrm{i}+2 \mathrm{j}-\mathrm{k}), \mathrm{OQ}(-\mathrm{i}+\mathrm{j}+\mathrm{k})$ को बाह्य $\mathrm{m}$ : $\mathrm{n}$ अनुपद मे विभाजित करने वाला बिन्दु $\mathrm{R}$ का स्थित सदिश

$\overrightarrow{\mathrm{OR}}=\dfrac{2(-\hat{\mathrm{i}}+\hat{\mathrm{k}})-1(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}})}{2-1}=(-2 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+2 \hat{\mathrm{k}})-(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}})$

$=-3 \hat{\mathrm{i}}+3 \hat{\mathrm{k}}$

16. दो बिदुओं $\mathrm{P}(2,3,4), \mathrm{Q}(4,1,-2)$ को मिलाने वाले सदिश का मध्य बिदु ज्ञात कीजिए। 

उत्तर: बिन्दु  $\mathrm{P}(2,3,4), \mathrm{Q}(4,1,-2)$ को मिलाने वाले सदिश का मध्य बिंदु

$\overrightarrow{\mathrm{OR}}=\dfrac{(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+4 \hat{\mathrm{k}})+(4 \hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}})}{2}=\dfrac{(2+4) \hat{\mathrm{i}}+(3+1) \hat{\mathrm{j}}+(4-2) \hat{\mathrm{k}}}{2}$

$=\dfrac{6 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}}{2}=3 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}}$

17. दर्शाइए कि बिंदु $A, B, C$ जिनके स्थिति सदिश क्रमशः $a=3 i-4 j-4 k, b=2 i-j+k, c=i-3 j-5 k$ है, एक समकोण त्रिभुज के शिर्षो का निर्माण करते है।

उत्तर: $a=3 i-4 j-4 k, b=2 i-j+k, c=i-3 j-5 k$

$\overrightarrow{\mathrm{AB}}=\mathrm{b}-\mathrm{a}=(2-3) \hat{\mathrm{i}}+(-1+4) \hat{\mathrm{j}}+(1+4) \hat{\mathrm{k}}=-\hat{\mathrm{i}}+3 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}$

$\overrightarrow{\mathrm{BC}}=\mathrm{c}-\mathrm{b}=(1-2) \hat{\mathrm{i}}+(-3+1) \dot{\mathrm{j}}+(-5-1) \hat{\mathrm{k}}=-\hat{\mathrm{i}}-2 \hat{\mathrm{j}}-6 \hat{\mathrm{k}}$

$\overline{\mathrm{CA}}=\mathrm{a}-\mathrm{c}=(3-1) \hat{\mathrm{i}}+(-4+3) \hat{\mathrm{j}}+(-4+5) \hat{\mathrm{k}}=2 \mathrm{i}-\hat{\mathrm{j}}+\hat{\mathrm{k}}$

$|\overrightarrow{\mathrm{AB}}|^{2}=-(-1)^{2}+3^{2}+5^{2}=-1+9+25=35$

$|\overrightarrow{\mathrm{BC}}|^{2}=(-1)^{2}+(-2)^{2}+(-6)^{2}=1+4+36=41$

$|\overrightarrow{\mathrm{CA}}|^{2}=2^{2}+(-1)^{2}+1^{2}=4+1+1=6$

$|\overrightarrow{\mathrm{AB}}|^{2}+|\overrightarrow{\mathrm{CA}}|^{2}=35+6=41=|\overrightarrow{\mathrm{BC}}|^{2}$

इसी कारण त्रिकोण $\mathrm{ABC}$ समकोण है।

18. त्रिभुज ABC के लिए निम्नलिखित मे से कौन सा कथं सत्य नहीं है। 

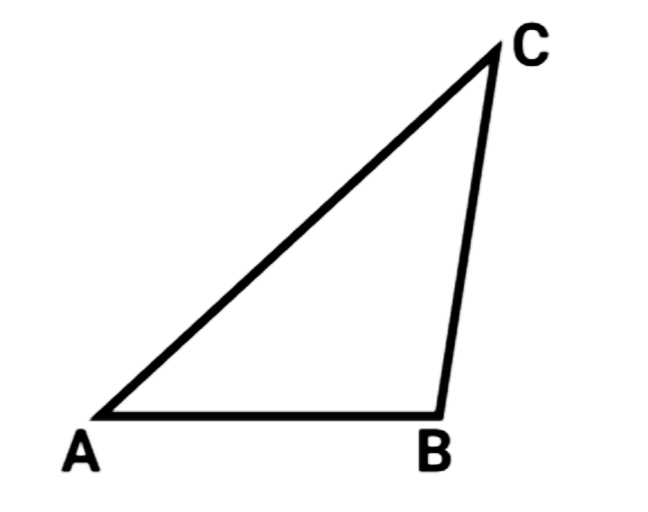
(a) ${{AB + BC + CA  =  0}}$

(b) ${{AB + BC - AC  =  0}}$

(c) ${{AB + BC - CA  =  0}}$

(d) ${{AB - CB + CA  =  0}}$

उत्तर: $\mathrm{AB}+\mathrm{BC}=-\mathrm{CA}$

$\mathrm{AB}+\mathrm{BC}+\mathrm{CA}=0^{\circ}$

तो विकल्प (a) सत्य है।

$\mathrm{AB}+\mathrm{BC}=\mathrm{AC}$

$\mathrm{AB}+\mathrm{BC}-\mathrm{AC}=0 \ldots \ldots \cdots \cdots(2)$

तो विकल्प (b) सत्य है।

(2) से हमे मिलेगा $\mathrm{AB}-\mathrm{CB}+\mathrm{CA}=0$

तो विकल्प (d) सत्य है।

अब (c) से

$\mathrm{AB}+\mathrm{BC}-\mathrm{CA}=\mathrm{O}$

$\mathrm{AB}+\mathrm{BC}=\mathrm{CA}$

(1) और (3) से मिलेगा

$\mathrm{AC}=\mathrm{CA}$

$\mathrm{AC}=-\mathrm{AC}$

$\mathrm{AC}+\mathrm{AC}=0$

$2 \mathrm{AC}=\overline{0}$

$\overline{\mathrm{AC}}=\overline{0}$

जो गलत है।

अतः (c) सत्य नहीं है।

19. यदि a और b दो संरेख सदिश है तो निम्नलिखित मे से कौन सा कथन सही नहीं है:

(a) ${{b  =  a}}$ किसी अदिश के लिए 

(b) ${{a  =  b}}$ 

(c) ${{a,}}\;{{b}}$ के क्रमागत घटक समानुपती नहीं है। 

(d) दोनों सदिश ${{a,}}\;{{b}}$ की दिशा समान है परंतु विभिन्न है। 

उत्तर: विकल्प (d) सही नहीं है कारण अगर a, b दो संरेख सदिश है तो यह जरूरी नहीं की वह दोनों सदिश एक ही दिशा मे हो। उनकी दिशा अलग हो सकती है। 

कारण :

$b=\lambda a$

$\lambda=\pm 1, a=\pm b$

$\bar{a}=a_{1} \hat{i}+a_{2} \hat{j}+a_{3} \hat{k}, b=b_{1} \hat{i}+b_{2} \hat{j}+b_{3} \hat{k}$

$\bar{b}=\lambda a$

$b_{1} \hat{i}+b_{2} \hat{j}+b_{3} \hat{k}=\lambda\left(a_{1} i+a_{2} j+a_{3} \hat{k}\right)$

$b_{1} \hat{i}+b_{2} \hat{j}+b_{3} \hat{k}=\left(\lambda a_{1}\right) \hat{i}+\left(\lambda a_{2}\right) \hat{j}+\left(\lambda a_{3}\right) \hat{k}$

$b_{1}=\lambda a_{1}, b_{2}=\lambda a_{2}, b_{3}=\lambda a_{3}$

$\dfrac{b_{1}}{a}=\dfrac{b_{2}}{a_{2}}=\dfrac{b_{3}}{a_{3}}=\lambda$

प्रश्नावली 10.3

1. दो सदिशों $\vec{a}, \vec{b}$ के परिणाम क्रमश: $\sqrt{3}, 2$ है और $\vec{a} \cdot \vec{b}=\sqrt{6}$ है तो $\vec{a}, \vec{b}$ के बीच का कोण ज्ञात कीजिए।

उत्तर: मान लीजिए सदिश $\vec{a}, \vec{b}$ के बीच $\theta$ कोण है, तो

$\cos \theta=\dfrac{\vec{a} \times \vec{b}}{|\vec{a}| \vec{b}|}$

$\because \vec{a} \times \vec{b}=\sqrt{6},|\vec{a}|=\sqrt{3},|\vec{b}|=2$ 

$\therefore \cos \theta=\dfrac{\sqrt{6}}{(\sqrt{3})(2)}=\dfrac{(\sqrt{3})(\sqrt{2})}{(\sqrt{3})(2)}=\dfrac{1}{\sqrt{2}}=\cos \dfrac{\pi}{4}$

$\theta=\dfrac{\pi}{4}$

2. सदिशों $\hat{1}-2 \hat{j}+3 \hat{k}, 3 \hat{1}-2 \hat{j}+\hat{k}$ के बीच का कोण ज्ञात कीजिए।

उत्तर: माना $\overrightarrow{\mathrm{a}}=(\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$

तथा $\vec{b}=(3 \hat{1}-2 \hat{j}+\hat{k})$

और माना सदिश $\vec{a}, \vec{b}$ के बीच $\theta$ कोण है, तो

$\cos \theta=\dfrac{\vec{a} \times \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{(\hat{i}-2 \hat{j}+3 \hat{k}) \times(3 \hat{i}-2 \hat{j}+\hat{k})}{|\hat{1}-2 \hat{j}+3 \hat{k}||(3 \hat{1}-2 \hat{j}+\hat{k})|} \mid$

$=\dfrac{1.3+(-2)(-2)+3.1}{\sqrt{1^{2}+(-2)^{2}+3^{2}} \sqrt{1^{2}+(-2)^{2}+3^{2}}}$

$=\dfrac{3+4+3}{\sqrt{1+4+9} \sqrt{9+4+1}}$

$=\dfrac{10}{14}=\dfrac{5}{7}$

$\theta=\cos ^{-1} \dfrac{5}{7}$

3. सदिश $\hat{1}+\hat{j}$ पर सदिश $\hat{1}-\hat{j}$ का प्रक्षेप ज्ञात कीजिए।

उत्तर: मान लीजिए $\vec{a}=\hat{1} \hat{j}, \vec{b}=\hat{1}+\hat{j}$ $\vec{a}$ का $\vec{b}$ पर प्रक्षेप

$=\dfrac{\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}}{|\overrightarrow{\mathrm{b}}|}=\dfrac{(\hat{1} \hat{\mathrm{j}}) \times(\hat{1}+\hat{\mathrm{j}})}{|\hat{1}+\hat{\mathrm{j}}|}$

$=\dfrac{1-1}{\sqrt{2}}=\dfrac{0}{\sqrt{2}}$

$=0$

4. सदिश $\hat{1}+3 \hat{j}+7 \hat{k}$ का सदिश $7 \hat{1} \hat{-j}+8 \hat{k}$ पर प्रक्षेप ज्ञात कीजिए। 

उत्तर: माना $\vec{a}=\hat{1}+3 \hat{j}+7 \hat{k}$ तथा $\vec{b}=7 \hat{1} \hat{j}+8 \hat{k}$

$\vec{a}$ का $\vec{b}$ पर प्रक्षेप

$=\dfrac{\vec{a} \times \vec{b}}{|\vec{b}|}=\dfrac{(\hat{i}+3 \hat{j}+7 \hat{k})(7 \hat{1} \hat{j}+8 \hat{k})}{|7 \hat{1} \hat{j}+8 \hat{k}|}$

$=\dfrac{1.7+3(-1)+7.8}{\sqrt{7^{2}+(-1)^{2}+8^{2}}}=\dfrac{7-3+56}{\sqrt{49+1+64}}$

$=\dfrac{60}{\sqrt{114}}$

5. दर्शाइए की दिए हुए निम्नलिखित तीन सदिशों मे से प्रत्येक मात्रक सदिश है: $\dfrac{1}{7}(2 \hat{1}+3 \hat{j}+6 \hat{k}), \dfrac{1}{7}(3 \hat{1}-6 \hat{j}+2 \hat{k}), \dfrac{1}{7}(6 \hat{1}+2 \hat{j}-3 \hat{k})$ यह भी दर्शाइए कि ये सदिश परस्पर एक दूसरे के लम्बवत है।

उत्तर: माना $\overrightarrow{\mathrm{a}}=\dfrac{1}{7}(2 \hat{1}+3 \hat{\mathrm{j}}+6 \hat{\mathrm{k}}), \overrightarrow{\mathrm{b}}=\dfrac{1}{7}\left(3 \hat{1}-(\hat{\mathrm{j}}+2 \hat{\mathrm{k}}), \overrightarrow{\mathrm{c}}=\dfrac{1}{7}(6 \hat{1}+2 \hat{\mathrm{j}}-3 \hat{\mathrm{k}})\right.$

अब $|\vec{a}|=\dfrac{1}{7} \sqrt{2^{2}+3^{2}+6^{2}}=\dfrac{\sqrt{49}}{7}=\dfrac{7}{7}=1$

$|\vec{b}|=\dfrac{1}{7} \sqrt{3^{2}+(-6)^{2}+2^{2}}=\dfrac{\sqrt{49}}{7}=\dfrac{7}{7}=1$

$|\vec{c}|=\dfrac{1}{7} \sqrt{6^{2}+2^{2}+(-3)^{2}}=\dfrac{\sqrt{49}}{7}=\dfrac{7}{7}=1$

चुकी तीनों सदिशों $\vec{a}, \vec{b}, \vec{c}$ का परिणाम 1 है।

ये सदिश मात्रक सदिश है।

इति सिद्धम।

सदिश $\vec{a}$ सदिश $\vec{b}$ है के लम्बवत होगा यदि $\vec{a} \times \vec{b}=0$

अर्थात $\vec{a} \times \vec{b}=\left[\dfrac{1}{7}(2 \hat{1}+3 \hat{j}+6 \hat{k}) \times \dfrac{1}{7}(3 \hat{1}-6 \hat{j}+2 \hat{k})\right]$

$=\dfrac{1}{49}[2(3)+(3)(-6)+(6)(2)]$

$=\dfrac{1}{49}(6-18+12)=0$

$\vec{b} \times \vec{c}=\left[\dfrac{1}{7}(3 \hat{1}-6 \hat{j}+2 \hat{k}) \times \dfrac{1}{7}(6 \hat{1}+2 \hat{j}-3 \hat{k})\right]$

$=\dfrac{1}{49}[(3)(6)+(-6)(2)+(2)(-3)]$

$=\dfrac{1}{49}(18-12-6)=0$

$\vec{c} \times \vec{a}=\left[\dfrac{1}{7}(6 \hat{i}+2 \hat{j}-3 \hat{k}) \times \dfrac{1}{7}(2 \hat{1}+3 \hat{j}+6 \hat{k})\right]$

$=\dfrac{1}{49}[(6)(2)+(2)(3)+(-3)(6)]$

$=\dfrac{1}{49}[12+6-18]=0$

$\vec{a} \times \vec{b}, \vec{b} \times \vec{c}, \vec{c} \times \vec{a}$ मे प्रत्येक का मान शून्य है।

$\therefore \overrightarrow{\mathrm{a}} \perp \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{b}} \perp \overrightarrow{\mathrm{c}}, \overrightarrow{\mathrm{c}} \perp \overrightarrow{\mathrm{a}}$

अतः $\vec{a}, \vec{b}, \vec{c}$ परस्पर लमबवत है।

इति सिद्धम।

6. यदि $(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})=8$ और $|\vec{a}|=8|\vec{b}|$ हो तो $|\vec{a}|,|\vec{b}|$ ज्ञात कीजिए।

उत्तर: दिया है $(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})=8$

$\Rightarrow \vec{a} \times \vec{a}-\vec{a} \times \vec{b}+\vec{b} \times \vec{a}-\vec{b} \times \vec{b}=8$

परंतु $\vec{a} \times \vec{b}=\vec{b} \times \vec{a}$

$\therefore \vec{a} \times \vec{a}-\vec{a} \times \vec{b}+\vec{a} \times \vec{b}-\vec{b} \times \vec{b}=8$

$\vec{a} \times \vec{a} \cdot \vec{b} \times \vec{b}=8$

$64|\vec{b}|^{2}-\left.\vec{b}\right|^{2}=8 \quad[\because|\vec{a}|=8|\vec{b}|]$

$63|\vec{b}|^{2}=8$

$\therefore|\vec{b}|=\sqrt{\dfrac{8}{63}}=\dfrac{2}{3} \sqrt{\dfrac{2}{7}}$

$|\vec{a}|=8|\vec{b}|=8 \times \dfrac{2}{3} \sqrt{\dfrac{2}{7}}=\dfrac{16}{3} \sqrt{\dfrac{2}{7}}$

7. $(3 \vec{a}-5 \vec{b}) \times(2 \vec{a}+7 \vec{b})$ का मान ज्ञात कीजिए।

उत्तर: दिया है $(3 \vec{a}-5 \vec{b}) \times(2 \vec{a}+7 \vec{b})$

$=(3 \vec{a}) \times(2 \vec{a})+(3 \vec{a}) \times(7 \vec{b})+(-5 \vec{b}) \times(2 \vec{a})+(-5 \vec{b}) \times(7 \vec{b})$

$=6|\vec{a}|^{2}+21(\vec{a} \times \vec{b})-10(\vec{b} \times \vec{a})-35|\vec{b}|^{2} \quad[\because \vec{a} \times \vec{b}=\vec{b} \times \vec{a}]$

$=6|\vec{a}|^{2}+21(\vec{a} \times \vec{b})-10(\vec{a} \times \vec{b})-35|\vec{b}|^{2}$

$=6|\vec{a}|^{2}+11(\vec{a} \times \vec{b})-35|\vec{b}|^{2}$

8. दो सदिशों $\vec{a}, \vec{b}$ के परिणाम ज्ञात कीजिए यदि इनके परिणाम समान है और इन के बीच का कोण $60^{\circ}$ है तथा उनका अदिश गुणनफल $\dfrac{1}{2}$ है।

उत्तर: दिया है $\theta=60^{\circ}, \vec{a} \times \vec{b}=\dfrac{1}{2},|\vec{a}|=|\vec{b}|$

सदिश $\vec{a}, \vec{b}$ के बीच का कोण यदि $\theta$ हो तो

$\cos \theta=\dfrac{\vec{a} \times \vec{b}}{|\vec{a}||\vec{b}|}$

$\cos 60^{\circ}=\dfrac{\dfrac{1}{2}}{|\vec{a}|^{2}} ; \dfrac{1}{2}=\dfrac{1}{2|\vec{a}|^{2}}$

$|\vec{a}|^{2}=1 ;|\vec{a}|=1$

$|\vec{a}|=1,|\vec{b}|=1$

9. यदि एक मात्रक सदिश $\vec{a}$ के लिए $(\vec{x}-\vec{a}) \times(\vec{x}+\vec{a})=12$ हो तो $|\vec{x}|$ ज्ञात कीजिए। 

उत्तर: दिया है $(\vec{x}-\vec{a}) \times(\vec{x}+\vec{a})=12$

$(\overrightarrow{\mathrm{x}}-\overrightarrow{\mathrm{a}}) \times(\overrightarrow{\mathrm{x}}+\overrightarrow{\mathrm{a}})=12$

$\overrightarrow{\mathrm{x}} \times \overrightarrow{\mathrm{x}}+\overrightarrow{\mathrm{x}} \times \overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{x}}-\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{a}}=12$

$|\overrightarrow{\mathrm{x}}|^{2}-\left.\overrightarrow{\mathrm{a}}\right|^{2}=12 \quad[\because \overrightarrow{\mathrm{x}} \times \overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{x}}]$

$|\overrightarrow{\mathrm{x}}|^{2}-1=12 \quad[\because|\vec{a}|=1]$

$|\mathrm{x}|^{2}=13$

$|\overrightarrow{\mathrm{x}}|=\sqrt{13}$

10. यदि $\vec{a}=2 \hat{1}+2 \hat{j}+3 \hat{k}, \vec{b}=-\hat{1}+2 \hat{j}+\hat{k}, \vec{c}=3 \hat{i}+\hat{j}$ इस प्रकार है की $\vec{a}+\lambda \vec{b}, \vec{c}$ पर लंब है तो $\lambda$ का मान ज्ञात कीजिए।

उत्तर: दिया है $\vec{a}=2 \hat{1}+2 \hat{j}+3 \hat{k}, \vec{b}=-\hat{i}+2 \hat{j}+\hat{k}$

$\vec{a}+\lambda \vec{b}=(2 \hat{1}+2 \hat{j}+3 \hat{k})+\lambda(-\hat{1}+2 \hat{j}+\hat{k})$

$=(2-\lambda) \hat{i}+(2+2 \lambda) \hat{j}+(3+\lambda) \hat{k}$

$\vec{a}+\lambda \vec{b}, \vec{c}=3 \hat{1}+\hat{j}$

$\vec{a}+\lambda \vec{b} \perp \vec{c}$

$(\vec{a}+\lambda \vec{b}) \times(\vec{c})=0$

${[(2-\lambda) \hat{1}+(2+2 \lambda) \hat{j}+(3+\lambda) \hat{k}][3 \hat{i}+\hat{j}]=0}$

$3(2-\lambda)+(2+2 \lambda) \times 1+(3+\lambda) \times 0=0$

$6-3 \lambda+2+2 \lambda=0$

$\lambda=8$

11. दर्शाइए की दो शून्यतर सदिश $\vec{a}, \vec{b}$ के लिए $|\vec{a}| \vec{b}+|\vec{b}| \vec{a},|\vec{a}| \vec{b}-|\vec{b}| \vec{a}$ पर लंब है। 

उत्तर: दिया है $|\vec{a}| \vec{b}+|\vec{b}| \vec{a},|\vec{a}| \vec{b}-|\vec{b}| \vec{a}$ पर लंब है

यदि $[|\vec{a}| \vec{b}+|\vec{b}| \vec{a}] \times[|\vec{a}| \vec{b}-|\vec{b}| \vec{a}]=0$

$=|\vec{a}| \vec{b} \times|\vec{a}| \vec{b}-|\vec{a}| \vec{b}|\vec{b}| \vec{a}+\left.|\vec{b}| \vec{a}|\vec{b} \times \vec{a}-| \vec{b}\right|^{2} \vec{a} \times \vec{a}$

$=|\vec{a}|^{2} \vec{b} \times \vec{b}-\left.\vec{a}|| \vec{b}|\vec{a} \times \vec{b}+| \vec{b}|| \vec{a}|\vec{a} \times \vec{b}-| \vec{b}\right|^{2}|\vec{a}|^{2}$

$=|\vec{a}|^{2}|\vec{b}|^{2}-|\vec{a}|^{2}|\vec{b}|^{2}=0$

अतः दिए गए सदिश एक दूसरे पर लंब है।

इति सिद्धम।

12. यदि $\vec{a} \times \vec{a}=0, \vec{a} \times \vec{b}=0$ तो सदिश $\vec{b}$ के बारे मे क्या निष्कर्ष निकाला जा सकता है। 

उत्तर: $\vec{a} \times \vec{a}=0, \vec{a} \times \vec{b}=0$

$\vec{a} \times \vec{a}=0$

$|\vec{a}|^{2}=0$

$|\vec{a}|=0, \vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \cos \theta=0$

अतः $\vec{b}$ कोई भी सदिश हो सकता है।

13. यदि $\vec{a}, \vec{b}, \vec{c}$ मात्रक सदिश इस प्रकार है की $\vec{a}+\vec{b}+\vec{c}=0$ तो $\vec{a} \times \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} . \vec{a}$ का मान ज्ञात कीजिए।

उत्तर: $\vec{a}, \vec{b}, \vec{c}$ मात्रक सदिश है।

$|\vec{a}|=|\vec{b}|=|\vec{c}|=1$

$\vec{a}+\vec{b}+\vec{c}=0$

$\vec{a}+\vec{b}=-\vec{c} \ldots \ldots \ldots(i)$

$\vec{a} \times(\vec{a}+\vec{b})=\vec{a} \times(-\vec{c})$

$\vec{a} \times \vec{a}+\vec{a} \times \vec{b}=-\vec{a} \times \vec{c}$

$|\vec{a}|^{2}+\vec{a} \times \vec{b}+\vec{c} \times \vec{a}=0$

$\vec{a} \times \vec{b}+\vec{c} \times \vec{a}=-1 \ldots \ldots$

पुन: समीकरण (i) से

$\overrightarrow{\mathrm{b}} \times(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}})=\overrightarrow{\mathrm{b}} \times(-\overrightarrow{\mathrm{c}})$

$\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathbf{a}}+\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{b}}=-\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}$

$\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}+|\overrightarrow{\mathrm{b}}|^{2}=0$

$\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}=-1 \ldots \ldots  { (iii)}$

पुन: समीकरण (i) से

$\overrightarrow{\mathrm{c}} \times(\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}})=\overrightarrow{\mathrm{c}} \times(-\overrightarrow{\mathrm{c}})$

$\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathbf{a}}+\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{b}}=-\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{c}}$

$\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{b}}+|\overrightarrow{\mathrm{c}}|^{2}=0$

$\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{b}}=-1 \ldots \ldots  { (iv) }$

समीकरण (i) और (iv) को जोड़ने पर

$2(\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a})=-3$

$\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}=-\dfrac{3}{2}$

14. यदि $\vec{a}=0$ अथवा $\vec{b}=0$ तब $\vec{a} \times \vec{b}=0$ परंतु विलोम का सत्य होना आवश्यक नहीं है। एक उदाहरण द्वारा अपने उत्तर की पुष्टि कीजिए।

उत्तर: दिया है जब $\vec{a}=0$ अथवा $\vec{b}=0$ तब $\vec{a} \times \vec{b}=0$ परंतु यदि $\vec{a} \times \vec{b}=0$ हो तो $\vec{a}, \vec{b}$ का शून्य होना सत्य नहीं है।

मान लीजिए $\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \vec{b}=\hat{i}+3 \hat{j}+5 \hat{k}$

$|\vec{a}|=\sqrt{1^{2}+(-2)^{2}+1^{2}}=\sqrt{6}$

$|\vec{b}|=\sqrt{1^{2}+3^{2}+5^{2}}=\sqrt{35}$

$\vec{a} \times \vec{b}=(\hat{1}-2 \hat{j}+\hat{k})(1+3 \hat{j}+5 \hat{k})=1.1-2.3+1.5=0$

अतः $\vec{a} \times \vec{b}=0$ परंतु $\vec{a} \neq 0, \vec{b} \neq 0$

15. यदि किसी त्रिभुज $A B C$ के शीर्ष $A, B, C$ क्रमश: $(1,2,3),(-1,0,0),(0,1,2)$ है तो $\angle A B C$ ज्ञात कीजिए। $\angle \mathrm{ABC}$ संदेशों $\overrightarrow{\mathrm{BA}}, \overrightarrow{\mathrm{BC}}$ के बीच का कोण है।

उत्तर: मान लीजिए $O$ मूल बिन्दु हो तो $A$ का स्थिति सदिश, $\overrightarrow{\mathrm{OA}}=\hat{1}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}, \mathrm{B}$ का स्थिति सदिश $\overrightarrow{\mathrm{OB}}=-\hat{1}$

तथा $C$ का स्थिति सदिश, $\overrightarrow{\mathrm{OC}}=\hat{\mathrm{j}}+2 \hat{\mathrm{k}}$

$\overrightarrow{\mathrm{BA}}=\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}=(\hat{1}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})+\hat{1}$

$=2 \hat{1}+2 \hat{j}+3 \hat{\mathrm{k}}$

$|\overrightarrow{\mathrm{BA}}|=\sqrt{2^{2}+2^{2}+3^{2}}=\sqrt{4+4+9}=\sqrt{17}$

$\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}=(\hat{j}+2 \hat{k})-(-\hat{1})$

$=\hat{1}+\hat{j}+2 \hat{k}$

$|\overrightarrow{\mathrm{BC}}|=\sqrt{1^{2}+1^{2}+2^{2}}=\sqrt{1+1+4}=\sqrt{6}$

सदिश $\overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{BA}}$ के बीच कोण $\angle \mathrm{ABC}$

$\cos \mathrm{ABC}=\dfrac{\overrightarrow{\mathrm{BC}} \times \overrightarrow{\mathrm{BA}}}{|\overrightarrow{\mathrm{BC}}| \overrightarrow{\mathrm{BA}}|}$

$=\dfrac{(\hat{1}+\hat{\mathbf{j}}+2 \hat{\mathrm{k}}) \times(2 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})}{\sqrt{6} \times \sqrt{7}}$

$=\dfrac{2.1+2 \times 1+3.2}{\sqrt{102}}=\dfrac{10}{\sqrt{102}}$

$\angle \mathrm{ABC}=\cos ^{-1}\left(\dfrac{10}{\sqrt{102}}\right)$

16. दर्शाइए की बिन्दु $\mathrm{A}(1,2,7), \mathrm{B}(2,6,3), \mathrm{C}(3,10,-1)$ संरेख है। 

उत्तर: दिए गए बिन्दुओ के स्थिति सदिश

$\overrightarrow{\mathrm{OA}}=\hat{1}+2 \hat{\mathrm{j}}+7 \hat{\mathrm{k}}, \overrightarrow{\mathrm{OB}}=2 \hat{1}+6 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}$

$\overrightarrow{\mathrm{OC}}=3 \hat{\mathrm{i}}+10 \hat{\mathrm{j}}-\hat{\mathrm{k}}$

$\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}$

$=(2 \hat{1}+6 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})-(\hat{1}+2 \hat{\mathrm{j}}+7 \hat{\mathrm{k}})$

$=\hat{1}+4 \hat{\mathrm{j}}-4 \hat{\mathrm{k}}$

$\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}$

$=(3 \hat{1}+10 \hat{\mathrm{j}} \hat{\mathrm{k}})-(2 \hat{1}+6 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$

$=\hat{1}+4 \hat{j}-4 \hat{k}$

$\overrightarrow{A C}=\overrightarrow{O C}-\overrightarrow{O A}$

$=(3 \hat{i}+10 \hat{j}-\hat{k})-(\hat{1}+2 \hat{j}+7 \hat{k})$

$=2 \hat{i}+8 \hat{j}-8 \hat{k}$

$=2(\hat{i}+4 \hat{j}-4 \hat{k})$

अर्थात $\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{AC}}$ एक ही सदिश $\hat{i}+4 \hat{\mathrm{j}}-4 \hat{\mathrm{k}}$ को निरूपित करते है। अतः $\mathrm{A}, \mathrm{B}, \mathrm{C}$ संरेख है।

इति सिद्धम।

17. दर्शाइए की सदिश $2 \hat{1}-\hat{j}+\hat{k}, \hat{1}-3 \hat{j}-5 \hat{k}, 3 \hat{1}-4 \hat{j}-4 \hat{k}$ एक समकोण त्रिभुज के शीर्षों की रचना करते है। 

उत्तर: मान लीजिए दिए हुए सदिशों $2 \hat{1} \hat{j}+\hat{k}, \hat{1}-3 \hat{j}-5 \hat{k}, 3 \hat{1}-4 \hat{j}-4 \hat{k}$ को क्रमश: $A, B, C$ से व्यक्त करे, $A$ का स्थिति संदिश $\overrightarrow{\mathrm{OA}}=2 \hat{1} \hat{\mathrm{j}}+\hat{\mathrm{k}}$

$\mathrm{B}$ का स्थिति संदिश $\overrightarrow{\mathrm{OB}}=\hat{1}-3 \hat{\mathrm{j}}-5 \hat{\mathrm{k}}$

$\mathrm{C}$ का स्थिति संदिश $\overrightarrow{\mathrm{OC}}=3 \hat{1}-4 \hat{\mathrm{j}}-4 \hat{\mathrm{k}}$

अब $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}$

$=(\hat{1}-3 \hat{j}-5 \hat{k})-(2 \hat{1}-\hat{j}+\hat{k})$

$=-1-2 \hat{j}+6 \hat{k}$

$|\overrightarrow{\mathrm{AB}}|=\sqrt{(1)^{2}+(-2)^{2}+(-6)^{2}}=\sqrt{1+4+36}=\sqrt{41}$

$\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OB}}=(3 \hat{1}-4 \hat{\mathrm{j}}-4 \hat{\mathrm{k}})-(\hat{1}-3 \hat{\mathrm{j}}-5 \hat{\mathrm{k}})=2 \hat{1} \hat{\mathrm{j}}+\hat{\mathrm{k}}$

$|\overrightarrow{\mathrm{BC}}|=\sqrt{(2)^{2}+(-1)^{2}+(1)^{2}}=\sqrt{6}$

$\overrightarrow{\mathrm{CA}}=\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OC}}=(2 \hat{1} \hat{\mathrm{j}}+\hat{\mathrm{k}})-(3 \hat{1}-4 \hat{\mathrm{j}}-4 \hat{\mathrm{k}})=-\hat{1}+3 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}$

$\overrightarrow{\mathrm{CA}} \mid=\sqrt{(-1)^{2}+(3)^{2}+(5)^{2}}=\sqrt{35}$

समकोण $\triangle \mathrm{ABC}$ के लिए जहा $\angle \mathrm{C}=90^{\circ}$ हो, तब

$|\overrightarrow{\mathrm{AB}}|^{2}=|\overrightarrow{\mathrm{BC}}|^{2}+|\overrightarrow{\mathrm{CA}}|^{2}$

$41=6+35=41$

अतः दिए गए सदिशों से एक समकोण त्रिभुज की रचना होती है।

इति सिद्धम।

18. यदि शुनयेतर सदिश $\vec{a}$ का परिणाम $a$ है और $\lambda$ एक शुनयेतर अदिश है तो $\lambda \vec{a}$ एक मात्रक सदिश है यदि

(a) $\lambda=1$

(b) $\lambda=-1$

(c) $\mathrm{a}=|\lambda|$

(d) $\mathrm{a}=\dfrac{1}{|\lambda|}$

उत्तर: दिया है : $\vec{a}$ का परिणाम $=a$

अर्थात $|\vec{a}|=a$

$\lambda \vec{a}$ एक मात्रक सदिश है

$|\lambda \vec{a}|=1$

$|\lambda||\vec{a}|=1$

$|\lambda| a=1$

$a=\dfrac{1}{|\lambda|}$

अतः विकल्प $(d)$ सही है।

प्रश्नावली 10.4

1. यदि ${{\vec a  =  \hat \imath  - 7\hat j + 7\hat k , \vec b  =  3\hat \imath  - 2\hat j + 2\hat k}}$ तो ज्ञात ${{|\vec a \times \vec b|}}$ कीजिए।

उत्तर: ${{\vec a  =  \hat \imath  - 7\hat j + 7\hat k , \vec b  =  3\hat \imath  - 2\hat j + 2\hat k}}$

${{\vec a \times \vec b  =  }}\left| {\begin{array}{*{20}{c}} {{{\hat \imath }}}&{{{\hat j}}}&{{{\hat k}}} \\ {{1}}&{{{ - 7}}}&{{7}} \\ {{3}}&{{{ - 2}}}&{{2}} \end{array}} \right|$

${{ =  \hat \imath ( - 14 + 14) - \hat j(2 - 21) + \hat k( - 2 + 21)}}$

${{ =  19\hat j + 19\hat k}}$

${{ =  |\vec a \times \vec b|  =  }}\sqrt {{{{{(19)}}}^{{2}}}{{ + (19}}{{{)}}^{{2}}}} {{  =  }}\sqrt {{{2 \times (19}}{{{)}}^{{2}}}} {{  =  19}}\sqrt {{2}}$

2. सदिश ${{\vec a + \vec b , \vec a - \vec b}}$ की लंब दिशा मे मात्रक सदिश ज्ञात कीजिए जहा ${{\vec a  =  3\hat \imath  + 2\hat j + 2\hat k , \vec b  =  \hat \imath  + 2\hat j - 2\hat k}}$ है।

उत्तर: ${{\vec a  =  3\hat \imath  + 2\hat j + 2\hat k , \vec b  =  \hat \imath  + 2\hat j - 2\hat k}}$

${{\vec a + \vec b  =  4\hat \imath  + 4\hat j , \vec a + \vec b  =  2\hat \imath  + 4\hat k}}$

${{(\vec a + \vec b) \times (\vec a + \vec b)  =  }}\left| {\begin{array}{*{20}{l}} {{{\hat \imath }}}&{{{\hat j}}}&{{{\hat k}}} \\ {{4}}&{{4}}&{{0}} \\ {{2}}&{{0}}&{{4}} \end{array}} \right|$

${{ =  16\hat \imath  - 16\hat j - 8\hat k}}$

${{|(\vec a + \vec b) \times (\vec a + \vec b)|  =  }}\sqrt {{{{{(16)}}}^{{2}}}{{ + ( - 16}}{{{)}}^{{2}}}{{ + ( - 8}}{{{)}}^{{2}}}} {{  =  24}}$

${{ =   \pm }}\dfrac{{{{(\vec a + \vec b) \times (\vec a + \vec b)}}}}{{{{|(\vec a + \vec b) \times (\vec a + \vec b)|}}}}{{  =  }}\dfrac{{{{16\hat i - 16\hat j - 8\hat k}}}}{{{{24}}}}{{  =   \pm }}\dfrac{{{2}}}{{{3}}}{{\hat \imath }} \mp \dfrac{{{2}}}{{{3}}}{{\hat j}} \mp \dfrac{{{2}}}{{{3}}}{{\hat k}}$

3. यदि एक मात्रक सदिश ${{\vec a , \hat \imath }}$ के साथ $\dfrac{{{\pi }}}{{{3}}}{{ , \hat j}}$ के साथ $\dfrac{{{\pi }}}{{{4}}}{{ , \hat k}}$ के साथ एक न्यून कोण ${{\theta }}$ बनाता है तो ${{\theta }}$ का मान ज्ञात कीजिए और इसकी सहायता से ${{\vec a}}$ के घटक भी ज्ञात कीजिए।

उत्तर:  ${{\vec a  =  }}{{{a}}_{{1}}}{{\hat \imath  + }}{{{a}}_{{2}}}{{\hat j + }}{{{a}}_{{3}}}{{\hat k , |\vec a|  =  1}}$

${{cos}}\dfrac{{{\pi }}}{{{3}}}{{  =  }}\dfrac{{{{{a}}_{{1}}}}}{{{{|\vec a|}}}}$

$\dfrac{{{1}}}{{{2}}}{{  =  }}{{{a}}_{{1}}}{{  [|\vec a|  =  1]}}$

${{cos}}\dfrac{{{\pi }}}{{{4}}}{{  =  }}\dfrac{{{{{a}}_{{2}}}}}{{{{|\vec a|}}}}$

$\dfrac{{{1}}}{{\sqrt {{2}} }}{{  =  }}{{{a}}_{{2}}}{{  [|\vec a|  =  1]}}$

${{cos\theta   =  }}\dfrac{{{{{a}}_{{3}}}}}{{{{|\vec a|}}}}$

${{{a}}_{{3}}}{{  =  cos\theta }}$

${{|a|  =  1}}$

$\sqrt {{{a}}_{{1}}^{{2}}{{ + a}}_{{2}}^{{2}}{{ + a}}_{{3}}^{{2}}} {{  =  1}}$

${\left( {\dfrac{{{1}}}{{{2}}}} \right)^{{2}}}{{ + }}{\left( {\dfrac{{{1}}}{{\sqrt {{2}} }}} \right)^{{2}}}{{ + co}}{{{s}}^{{2}}}{{\theta   =  1}}$

$\dfrac{{{1}}}{{{4}}}{{ + }}\dfrac{{{1}}}{{{2}}}{{ + co}}{{{s}}^{{2}}}{{\theta   =  1}}$

${{co}}{{{s}}^{{2}}}{{\theta   =  }}\dfrac{{{1}}}{{{4}}}$

${{cos\theta   =  }}\dfrac{{{1}}}{{{2}}}$

${{\theta   =  }}\dfrac{{{\pi }}}{{{3}}}$

${{{a}}_{{3}}}{{  =  cos}}\dfrac{{{\pi }}}{{{3}}}{{  =  }}\dfrac{{{1}}}{{{2}}}$

$\therefore \;\left( {\dfrac{{{1}}}{{{2}}}{{,}}\dfrac{{{1}}}{{\sqrt {{2}} }}{{,}}\dfrac{{{1}}}{{{2}}}} \right)$

4. दर्शाइए की ${{(\vec a + \vec b) \times (\vec a - \vec b)  =  2(\vec a \times \vec b)}}$

उत्तर: हमे यह सिद्ध करना है की ${{(\vec a + \vec b) \times (\vec a - \vec b)  =  2(\vec a \times \vec b)}}$

${{(\vec a + \vec b) \times (\vec a - \vec b)  =  (\vec a - \vec b) \times \vec a + (\vec a - \vec b) \times \vec b}}$

${{ =  \vec a \times \vec a - \vec b \times \vec a + \vec a \times \vec b - \vec b \times \vec b}}$

${{ =  2(\vec a \times \vec b)}}$

5. ${{\lambda  , \mu }}$ ज्ञात कीजिए, यदि ${{(2\hat \imath  + 6\hat j + 27\hat k) \times (\hat \imath  + \lambda \hat j + \mu \hat k)  =  \vec 0}}$

उत्तर: ${{(2\hat \imath  + 6\hat j + 27\hat k) \times (\hat \imath  + \lambda \hat j + \mu \hat k)  =  \vec 0}}$

$\left| {\begin{array}{*{20}{c}} {{{\hat \imath }}}&{{{\hat j}}}&{{{\hat k}}} \\ {{2}}&{{6}}&{{{27}}} \\ {{1}}&{{\lambda }}&{{\mu }} \end{array}} \right|{{  =  0\hat \imath  + 0\hat j + 0\hat k}}$

${{\hat \imath (6\mu  - 27\lambda ) - \hat j(2\mu  - 27) + \hat k(2\lambda  - 6)  =  0\hat \imath  + 0\hat j + 0\hat k}}$\

${{6\mu  - 27\lambda   =  0}}$

${{2\mu  - 27  =  0}}$

${{2\lambda  - 6  =  0}}$

${{\lambda   =  3}}$

${{2\mu  - 27  =  0}}$

${{\mu   =  }}\dfrac{{{{27}}}}{{{2}}}$

$\therefore {{ \lambda   =  3 , \mu   =  }}\dfrac{{{{27}}}}{{{2}}}$

6. दिया हुआ है की ${{\vec a \times \vec b  =  0 , \vec a \times \vec b  =  0}}$ सदिश ${{\vec a , \vec b}}$ के बारे मे आप क्या निष्कर्ष निकाल सकते है।

उत्तर: दिया हुआ है की ${{\vec a \times \vec b  =  0 , \vec a \times \vec b  =  0}}$

${{|\vec a|  =  0 ; |\vec b|  =  0 ; \vec a}} \bot {{\vec b}}$

${{\vec a \times \vec b  =  0}}$

${{|\vec a|  =  0 , |\vec b|  =  0 ; \vec a || \vec b}}$

${{\vec a \times \vec b  =  0}}$

7. मान लीजिए सदिश ${{\vec a , \vec b , \vec c}}$ क्रमश: ${{{a}}_{{1}}}{{\hat \imath  + }}{{{a}}_{{2}}}{{\hat j + }}{{{a}}_{{3}}}{{\hat k , }}{{{b}}_{{1}}}{{\hat \imath  + }}{{{b}}_{{2}}}{{\hat j + }}{{{b}}_{{3}}}{{\hat k , }}{{{c}}_{{1}}}{{\hat \imath  + }}{{{c}}_{{2}}}{{\hat j + }}{{{c}}_{{3}}}{{\hat k}}$ के रूप मे दिए हुए है तब दर्शाइए की ${{\vec a \times (\vec b + \vec c)  =  \vec a \times \vec b + \vec a \times \vec c}}$

उत्तर: दिया है ${{{a}}_{{1}}}{{\hat \imath  + }}{{{a}}_{{2}}}{{\hat j + }}{{{a}}_{{3}}}{{\hat k , }}{{{b}}_{{1}}}{{\hat \imath  + }}{{{b}}_{{2}}}{{\hat j + }}{{{b}}_{{3}}}{{\hat k , }}{{{c}}_{{1}}}{{\hat \imath  + }}{{{c}}_{{2}}}{{\hat j + }}{{{c}}_{{3}}}{{\hat k}}$

सिद्ध करना है ${{\vec a \times (\vec b + \vec c)  =  \vec a \times \vec b + \vec a \times \vec c}}$

${{\vec a  = }}{{{a}}_{{1}}}{{\hat \imath  + }}{{{a}}_{{2}}}{{\hat j + }}{{{a}}_{{3}}}{{\hat k}}$

${{\vec b  =  }}{{{b}}_{{1}}}{{\hat \imath  + }}{{{b}}_{{2}}}{{\hat j + }}{{{b}}_{{3}}}{{\hat k}}$

${{\vec c  =  }}{{{c}}_{{1}}}{{\hat \imath  + }}{{{c}}_{{2}}}{{\hat j + }}{{{c}}_{{3}}}{{\hat k}}$

${{(\vec b + \vec c)  =  }}\left( {{{{b}}_{{1}}}{{ + }}{{{c}}_{{1}}}} \right){{\hat \imath  + }}\left( {{{{b}}_{{2}}}{{ + }}{{{c}}_{{2}}}} \right){{\hat j + }}\left( {{{{b}}_{{3}}}{{ + }}{{{c}}_{{3}}}} \right){{\hat k}}$

${{\vec a \times (\vec b + \vec c)  =  }}\left| {\begin{array}{*{20}{c}}{{{\hat \imath }}}&{{{\hat j}}}&{{{\hat k}}} \\ {{{{a}}_{{1}}}}&{{{{a}}_{{2}}}}&{{{{a}}_{{3}}}} \\ {{{{b}}_{{1}}}{{ + }}{{{c}}_{{1}}}}&{{{{b}}_{{2}}}{{ + }}{{{c}}_{{2}}}}&{{{{b}}_{{3}}}{{ + }}{{{c}}_{{3}}}} \end{array}} \right|$

${{ =  \hat \imath }}\left[ {{{{a}}_{{2}}}{{{b}}_{{3}}}{{ + }}{{{a}}_{{2}}}{{{c}}_{{3}}}{{ - }}{{{a}}_{{3}}}{{{b}}_{{2}}}{{ - }}{{{a}}_{{3}}}{{{c}}_{{2}}}} \right]{{ + \hat j}}\left[ {{{ - }}{{{a}}_{{1}}}{{{b}}_{{3}}}{{ - }}{{{a}}_{{1}}}{{{c}}_{{3}}}{{ + }}} \right.\left. {{{{a}}_{{3}}}{{{b}}_{{1}}}{{ + }}{{{a}}_{{3}}}{{{c}}_{{1}}}} \right]{{ + \hat k}}\left[ {{{{a}}_{{1}}}{{{b}}_{{2}}}{{ + }}{{{a}}_{{1}}}{{{c}}_{{2}}}{{ - }}{{{a}}_{{2}}}{{{b}}_{{1}}}{{ - }}{{{a}}_{{2}}}{{{c}}_{{1}}}} \right]$ ............(i)

${{\vec a \times \vec b  =  }}\left| {\begin{array}{*{20}{c}} {{{\hat \imath}}}&{{{\hat j}}}&{{{\hat k}}} \\ {{{{a}}_{{1}}}}&{{{{a}}_{{2}}}}&{{{{a}}_{{3}}}} \\ {{{{b}}_{{1}}}}&{{{{b}}_{{2}}}}&{{{{b}}_{{3}}}} \end{array}} \right|$

${{ =  \hat \imath }}\left[ {{{{a}}_{{2}}}{{{b}}_{{3}}}{{ - }}{{{a}}_{{3}}}{{{b}}_{{2}}}} \right]{{ + \hat j}}\left[ {{{{a}}_{{1}}}{{{b}}_{{3}}}{{ - }}{{{a}}_{{3}}}{{{b}}_{{1}}}} \right]{{ + \hat k}}\left[ {{{{a}}_{{1}}}{{{b}}_{{2}}}{{ - }}} \right.{{n\& }}\left. {{{{a}}_{{2}}}{{{b}}_{{1}}}} \right]$............(ii)

${{\vec a \times \vec c  =  }}\left| {\begin{array}{*{20}{c}} {{{\hat \imath }}}&{{{\hat j}}}&{{{\hat k}}} \\ {{{{a}}_{{1}}}}&{{{{a}}_{{2}}}}&{{{{a}}_{{3}}}} \\ {{{{c}}_{{1}}}}&{{{{c}}_{{2}}}}&{{{{c}}_{{3}}}}\end{array}} \right|$

${{ =  \hat \imath }}\left[ {{{{a}}_{{2}}}{{{c}}_{{3}}}{{ - }}{{{a}}_{{3}}}{{{c}}_{{2}}}} \right]{{ + \hat j}}\left[ {{{{a}}_{{3}}}{{{c}}_{{1}}}{{ - }}{{{a}}_{{1}}}{{c}}} \right]{{ + \hat k}}\left[ {{{{a}}_{{1}}}{{{c}}_{{2}}}{{ - }}{{{a}}_{{2}}}{{{c}}_{{1}}}} \right]$ ..........(iii)

(ii) और (iii) जोड़ने पर

${{ =  \hat \imath }}\left[ {{{{a}}_{{2}}}{{{c}}_{{3}}}{{ - }}{{{a}}_{{3}}}{{{c}}_{{2}}}{{ + }}{{{a}}_{{2}}}{{{b}}_{{3}}}{{ - }}{{{a}}_{{3}}}{{{b}}_{{2}}}} \right]{{ + \hat j}}\left[ {{{{a}}_{{3}}}{{{c}}_{{1}}}{{ - }}{{{a}}_{{1}}}{{c + }}} \right.\left. {{{{a}}_{{1}}}{{{b}}_{{3}}}{{ - }}{{{a}}_{{3}}}{{{b}}_{{1}}}} \right]{{ + \hat k}}\left[ {{{{a}}_{{1}}}{{{c}}_{{2}}}{{ - }}{{{a}}_{{2}}}{{{c}}_{{1}}}{{ + }}{{{a}}_{{1}}}{{{b}}_{{2}}}{{ - }}{{{a}}_{{2}}}{{{b}}_{{1}}}} \right]$ ..........(iv)

(i) और (iv) से

${{\vec a \times (\vec b + \vec c)  =  \vec a \times \vec b + \vec a \times \vec c}}$

8. यदि ${{\vec a  =  \vec 0 , \vec b  =  \vec 0}}$ तब ${{\vec a \times \vec b  =  \vec 0}}$ होता है। क्या विलोम सत्य है? उदाहरण सहित अपने उतर की पुष्टि कीजिए।

उत्तर: मान लीजिए कि

${{\vec a  =  2\hat \imath  + 3\hat j + 4\hat k}}$

${{\vec b  =  4\hat \imath  + 6\hat j + 8\hat k}}$

${{\vec a \times \vec b  =  }}\left| {\begin{array}{*{20}{l}} {{{\hat \imath }}}&{{{\hat j}}}&{{{\hat k}}} \\ {{2}}&{{3}}&{{4}} \\ {{4}}&{{6}}&{{8}} \end{array}} \right|$

${{ =  \hat l(24 - 24) - \hat j(16 - 16) + \hat k(12 - 12)}}$

${{ =  0\hat \imath  + 0\hat j + 0\hat k  =  \vec 0}}$

${{|\vec a|  =  }}\sqrt {{{29}}} {{ , |\vec b|  =  }}\sqrt {{{116}}}$

इसका विलोम असत्य।

9. एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष ${{A(1,1,2), B(2,3,5), C(1,5,5)}}$ है।

उत्तर: ${{A(1,1,2), B(2,3,5), C(1,5,5)}}$

$\overrightarrow {{{AB}}} {{  =  \hat \imath  + 2\hat j + 3\hat k}}$

$\overrightarrow {{{BC}}} {{  =   - \hat \imath  + 2\hat j}}$

$\vartriangle {{ABC  =  }}\dfrac{{{1}}}{{{2}}}{{|}}\overrightarrow {{{AB}}} {{ \times }}\overrightarrow {{{BC}}} {{|}}$

${{|}}\overrightarrow {{{AB}}} {{ \times }}\overrightarrow {{{BC}}} {{|  =  }}\sqrt {{{61}}}$

$\vartriangle {{ABC  =  }}\dfrac{{\sqrt {{{61}}} }}{{{2}}}$

10. एक समांतर चतुर्भुज का छेत्रफल ज्ञात कीजिए जिसकी संलग्र भुजाये सदिश ${{\vec a  =  \hat \imath  - \hat j + 3\hat k , \vec b  =  2\hat \imath  - 7\hat j + \hat k}}$ द्वारा निर्धारित है।

उत्तर: ${{\vec a  =  \hat \imath  - \hat j + 3\hat k , \vec b  =  2\hat \imath  - 7\hat j + \hat k}}$

${{\vec a \times \vec b  =  }}\left| {\begin{array}{*{20}{c}} {{{\hat \imath }}}&{{{\hat j}}}&{{{\hat k}}} \\ {{2}}&{{3}}&{{4}} \\ {{4}}&{{6}}&{{8}} \end{array}} \right|$

${{ =  \hat \imath ( - 1 + 21) - \hat j(1 - 6) + \hat k( - 7 + 2)}}$

${{ =  20\hat \imath  + 5\hat j - 5\hat k}}$

${{|\vec a \times \vec b|  =  }}\sqrt {{{{{(20)}}}^{{2}}}{{ + }}{{{5}}^{{2}}}{{ + }}{{{5}}^{{2}}}} {{  =  15}}\sqrt {{2}}$

11. मान लीजिए सदिशा ${{\vec a , \vec b}}$ इस प्रकार है की ${{|\vec a|  =  3 , |\vec b|  =  }}\dfrac{{\sqrt {{2}} }}{{{3}}}$ तब ${{\vec a \times \vec b}}$ एक मात्रक सदिशा है यदि ${{\vec a , \vec b}}$ के बीच का कोण है:

(a) $\dfrac{{{\pi }}}{{{6}}}$

(b) $\dfrac{{{\pi }}}{{{4}}}$

(c) $\dfrac{{{\pi }}}{{{3}}}$

(d) $\dfrac{{{\pi }}}{{{2}}}$

उत्तर: ${{|\vec a|  =  3 , |\vec b|  =  }}\dfrac{{\sqrt {{2}} }}{{{3}}}$

${{|\vec a \times \vec b|  =  1}}$

${{|\vec a| |\vec b| |sin\theta \hat n|  =  1}}$

${{|\vec a| |\vec b| |sin\theta |  =  1}}$

${{3 \times }}\dfrac{{\sqrt {{2}} }}{{{3}}}{{ \times sin\theta   =  1}}$

${{sin\theta   =  }}\dfrac{{{1}}}{{\sqrt {{2}} }}$

${{\theta   =  }}\dfrac{{{\pi }}}{{{4}}}$

सही विकल्प (b) है ।

12. एक आयत के शीर्षों A, B C, D जिनके स्थिति सदिश क्रमश: ${{ - \hat \imath  + }}\dfrac{{{1}}}{{{2}}}{{\hat j + 4\hat k , \hat \imath  + }}\dfrac{{{1}}}{{{2}}}{{\hat j + 4\hat k , \hat \imath  - }}\dfrac{{{1}}}{{{2}}}{{\hat j + 4\hat k ,  - \hat \imath  - }}\dfrac{{{1}}}{{{2}}}{{\hat j + 4\hat k}}$ है का क्षेत्रफल है:

(a) $\dfrac{1}{2}$

(b) $1$

(c) $2$

(d) $4$

उत्तर: $\overrightarrow {{{OA}}} {{  =   - \hat \imath  + }}\dfrac{{{1}}}{{{2}}}{{\hat j + 4\hat k , }}\overrightarrow {{{OB}}} {{  =  \hat \imath  + }}\dfrac{{{1}}}{{{2}}}{{\hat j + 4\hat k , }}\overrightarrow {{{OC}}} {{  =   - \hat \imath  - }}\dfrac{{{1}}}{{{2}}}{{\hat j + 4\hat k}}$

$\overrightarrow {{{AB}}} {{  =  (1 + 1)\hat \imath  + }}\left( {\dfrac{{{1}}}{{{2}}}{{ - }}\dfrac{{{1}}}{{{2}}}} \right){{\hat j + (4 - 4)\hat k  =  2\hat \imath }}$

$\overrightarrow {{{BC}}} {{  =  (1 - 1)\hat \imath  + }}\left( {{{ - }}\dfrac{{{1}}}{{{2}}}{{ - }}\dfrac{{{1}}}{{{2}}}} \right){{\hat j + (4 - 4)\hat k  =   - \hat j}}$

$\overrightarrow {{{AB}}} {{ \times }}\overrightarrow {{{BC}}} {{  =  }}\left| {\begin{array}{*{20}{c}} {{{\hat \imath }}}&{{{\hat j}}}&{{{\hat k}}} \\ {{2}}&{{0}}&{{0}} \\ {{0}}&{{{ - 1}}}&{{0}} \end{array}} \right|{{  =   - 2\hat k}}$

${{|}}\overrightarrow {{{AB}}} {{ \times }}\overrightarrow {{{BC}}} {{|  =  }}\sqrt {{{{{( - 2)}}}^{{2}}}} {{  =  2}}$

विकल्प (c) सही उत्तर है।

प्रश्नावली 10.5

1. XY प्लेन मे एक यूनिट वेक्टर लिखिए, जो सकारात्मक के साथ का ${{30}}^\circ$ कोण बनाता है। x – ऐक्सिस की दिशा। 

उत्तर: यदि XY प्लेन मे r यूनिट वेक्टर है तो ${{r}}\;{{ = }}\;{{cos\theta i + sin\theta i}}$

यह ${{\theta }}$ x – यक्ष की सकारात्मक दिशा के साथ इकाई वेक्टर द्वारा बनाया गया कोण है। 

इसलिए ${{\theta }}$ = ${{30}}^\circ$

${{r}}\;{{ = }}\;{{cos30^\circ i + sin30^\circ i}}$

${{ =  }}\dfrac{{\sqrt {{3}} }}{{{2}}}{{i + }}\dfrac{{{1}}}{{{2}}}{{j}}$ 

इसलिए आवश्यक इकाई वेकटर है $\dfrac{{\sqrt {{3}} }}{{{2}}}{{i + }}\dfrac{{{1}}}{{{2}}}{{j}}$

2. बिन्दुओ मे शामिल होने वाले वेक्टर के अदिश घटकों और परिणाम का पता लगाए ${{P(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{,}}{{{z}}_{{1}}}{{) , Q(}}{{{x}}_{{2}}}{{,}}{{{y}}_{{2}}}{{,}}{{{z}}_{{2}}}{{)}}$

उत्तर: ${{P(}}{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{,}}{{{z}}_{{1}}}{{) , Q(}}{{{x}}_{{2}}}{{,}}{{{y}}_{{2}}}{{,}}{{{z}}_{{2}}}{{)}}$ से जोड़ने वाले वेक्टर मे प्राप्त किया जा सकता है 

PQ = Q की स्थिति वेक्टर – P की स्थिति वेक्टर ${{ =  (}}{{{x}}_2}{{ - }}{{{x}}_1}{{)i + (}}{{{y}}_2}{{ - }}{{{y}}_1}{{)j + (}}{{{z}}_2}{{ - }}{{{z}}_1}{{)k}}$

${{|PQ|  =  }}\sqrt {{{{{(}}{{{x}}_2}{{ - }}{{{x}}_1}{{)}}}^{{2}}}{{ + (}}{{{y}}_2}{{ - }}{{{y}}_1}{{{)}}^{{2}}}{{ + (}}{{{z}}_2}{{ - }}{{{z}}_1}{{{)}}^{{2}}}}$ 

इसलिए स्केलर घटक और दिए गए बिन्दुओ से जोड़ने वाले वेक्टर के परिमाण क्रमश: है 

${{\{ (}}{{{x}}_2}{{ - }}{{{x}}_1}{{),(}}{{{y}}_2}{{ - }}{{{y}}_1}{{), + (}}{{{z}}_2}{{ - }}{{{z}}_1}{{)\} }}$ , $\sqrt {{{{{(}}{{{x}}_2}{{ - }}{{{x}}_1}{{)}}}^{{2}}}{{ + (}}{{{y}}_2}{{ - }}{{{y}}_1}{{{)}}^{{2}}}{{ + (}}{{{z}}_2}{{ - }}{{{z}}_1}{{{)}}^{{2}}}}$

3. एक लड़की पश्चिम की और ${{4 km}}$ चलती है, फर वह ${{30}}^\circ$ किमी पूर्व मे एक दिशा मे ${{3 km}}$ चलती है उतर और रुक जाती है। अपने प्रारम्भिक बिन्दु से लड़की के विस्थापन का निर्धारण करे प्रस्थान। 

उत्तर: बता दे की O और B क्रमश: लड़की के प्रारम्भिक और अंतिम स्थान है। फर लड़की की स्थिति को दिखाया जा सकता है। 

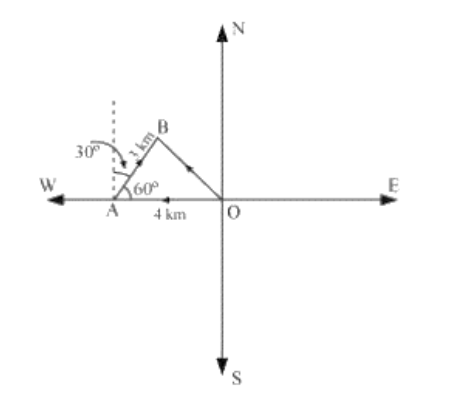
अब हमारे पास है: 

${{OA  =   - 4i}}$

${{AB  =  i|AB|cos6}}{{{0}}^{{^\circ }}}{{ + j|AB|Sin6}}{{{0}}^{{^\circ }}}$

${{ =  i \times 3 \times (1/2) + j \times 3 \times (}}\sqrt {{3}} {{/2)}}$

${{ =  (3/2)i + (3}}\sqrt {{3}} {{/2)j}}$ 

वेक्टर जोड़ के त्रिभुज नियम द्वारा हमारे पास:

${{OB  =  OA + AB}}$

${{ =  ( - 4i) + ((3/2)i + (3}}\sqrt {{3}} {{/2)j)}}$

${{ =  ( - 4 + (3/2))i + (3}}\sqrt {{3}} {{/2)j}}$

${{ =  (( - 8 + 3)/2)i + (3}}\sqrt {{3}} {{/2)j}}$

${{ =  ( - 5/2)i + (3}}\sqrt {{3}} {{/2)j}}$ 

इसलिए उसके प्रस्थान के प्रारम्भिक बिन्दु से लड़की का विस्थापन होता है ${{( - 5/2)i + (3}}\sqrt {{3}} {{/2)j}}$

4. यदि ${{a  =  }}\;{{b + c}}$ है तो क्या यह सच है की $\left| {{a}} \right|\;{{ = }}\;\left| {{b}} \right|{{ + }}\left| {{c}} \right|$ अपने जवाब का ओचित्य साबित करे। 

उत्तर: $\vartriangle {{ABC}}$ , ${{CB}}\;{{ = }}\;{{a}}\;{{,}}\;{{CA}}\,{{ = }}\;{{b}}\;{{,}}\;{{AB}}\;{{ = }}\,{{c}}$

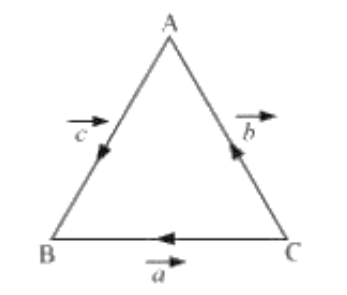
अब वेक्टर जोड़ के त्रिभुज नियम द्वारा हमारे पास है ${{a  =  }}\;{{b + c}}$

यह स्पष्ट रूप से ज्ञात है कि $\left| {{a}} \right|{{,}}\left| {{b}} \right|{{,}}\left| {{c}} \right|$ के पक्षों का प्रतिनिधित्व करते है $\vartriangle {{ABC}}$

साथ ही यह ज्ञात है की किसी त्रिभुज के किन्ही दो भुजाओ की लंबाई तीसरी भुज से अधिक है। 

$\left| {{a}} \right| < \left| {{b}} \right| + \left| {{c}} \right|$

इसलिए यह सच नहीं है $\left| {{a}} \right|\;{{ = }}\;\left| {{b}} \right|{{ + }}\left| {{c}} \right|$

5. ${{x}}$ का मान ज्ञात कीजिए जिसके लिए ${{x(i + j + k)}}$ एक इकाई सदिश है। 

उत्तर: ${{x(i + j + k)}}$ एक इकाई वेक्टर है यदि 

$\left| {{{x(i + j + k)}}} \right|\; = \;1$

$\sqrt {{{{x}}^{{2}}}{{ + }}{{{x}}^{{2}}} + {{{x}}^{{2}}}} {{  =  1}}$

$\sqrt {{{3}}{{{x}}^{{2}}}} {{  =  1}}$

$\sqrt {{3}} {{x  =  1}}$

${{x  =  (1/}}\sqrt {{3}} {{)}}$ 

इसलिए x का आवश्यक मान है ${{(1/}}\sqrt {{3}} {{)}}$

6. ${{5}}$ इकाइयों के परिणाम के वेक्टर का पता लगाए और वेक्टर के परिणाम  के समांतर ${{a  =  2i + 3j - k , b  =  i - 2j + k}}$

उत्तर: हमारे पास है ${{a  =  2i + 3j - k , b  =  i - 2j + k}}$

आज्ञा देना c और a का परिणाम है। 

फिर, 

${{c  =  a + b  =  (2 + 1)i + (3 - 2)j + ( - 1 + 1)k  =  3i + j}}$

${{|c|  =  }}\sqrt {{{{3}}^2} + {1^2}} {{  =  }}\sqrt {{9}} {{ + 1  =  }}\sqrt {{{10}}}$

${{C  =  (c/|c|)  =  (3i + j)/}}\sqrt {{{10}}}$ 

इसलिए परिणाम पाँच इकाइयों का वेक्टर और वेक्टर के परिणामों के समांतर a और b है 

${{ \pm 5}}{{.c  =   \pm 5 \times (1/}}\sqrt {{{10}}} {{)(3i + j)  =   \pm (3}}\sqrt {{{10i}}} {{)/2 \pm (}}\sqrt {{{10/2}}} {{)j}}$ 

7. यदि ${{a  =  i + j + k , b  =  2i - j + 3k , c  =  i - 2j + k}}$ तो वेक्टर ${{2a - b + 3c }}$ के संयंत्र एक इकाई वेक्टर खोजे। 

उत्तर: हमारे पास है ${{a  =  i + j + k , b  =  2i - j + 3k , c  =  i - 2j + k}}$

${{2a - b + 3c  =  2(i + j + k) - (2i - j + 3k) + 3(i - 2j + k)}}$

${{ =  3i - 3j + 2k}}$

${{|2a - b + 3c|  =  }}\sqrt {{{{3}}^2}{{ + ( - 3}}{{{)}}^{{2}}}{{ + }}{{{2}}^{{2}}}} {{  =  }}\sqrt {{{9 + 9 + 4}}} {{  =  }}\sqrt {{{22}}}$ 

इसलिए यूनिट वेक्टर के साथ ${{2a - b + 3c }}$

$\dfrac{(2a-b+3c)}{(2a-b+3c)}=\dfrac{(3i-3j+2k)}{\sqrt{{{22}}}}=\dfrac{3}{\sqrt{{{22}}}}i-\dfrac{3}{\sqrt{{{22}}}}j+\dfrac{2}{\sqrt{{{22}}}}k$

8. दिखाए की अंक ${{A(1, - 2, - 8) , B(5,0, - 2) , C(11,3,7)}}$ आपस मे टकरा रहे है, और वह अनुपद ज्ञात कीजिए जिसमे ${{B,AC}}$ को विभाजित करता है। 

उत्तर: दिए गए बिन्दु ${{A(1, - 2, - 8) , B(5,0, - 2) , C(11,3,7)}}$ है। 

${{AB  =  (5 - 1)i + (0 + 2)j + ( - 2 + 8)k  =  4i + 2j + 6k}}$

${{BC  =  (11 - 5)i + (3 - 0)j + (7 + 2)k  =  6i + 3j + 9k}}$

${{AC  =  (11 - 1)i + (3 + 2)j + (7 + 8)k  =  10i + 5j + 15k}}$

${{|AB|  =  }}\sqrt {{{{4}}^2}{{ + }}{{{2}}^{{2}}}{{ + }}{{{6}}^{{2}}}} {{  =  }}\sqrt {{{16 + 4 + 36}}} {{  =  }}\sqrt {{{56}}} {{  =  2}}\sqrt {{{14}}}$ 

${{|BC|  =  }}\sqrt {{{{6}}^2}{{ + }}{{{3}}^{{2}}}{{ + }}{{{9}}^{{2}}}} {{  =  }}\sqrt {{{36 + 9 + 81}}} {{  =  }}\sqrt {{{126}}} {{  =  3}}\sqrt {{{14}}}$

${{|AC|  =  }}\sqrt {{{1}}{{{0}}^{{2}}}{{ + }}{{{5}}^{{2}}}{{ + 1}}{{{5}}^{{2}}}} {{  =  }}\sqrt {{{100 + 25 + 225}}} {{  =  }}\sqrt {{{350}}} {{  =  5}}\sqrt {{{14}}}$

${{|AC|  =  |AB| + |BC}}\mid$ 

इस प्रकार दिए गए बिन्दु A, B, C आपस मे टकराते है। 

अब बिन्दु B को अनुपाद मे AC को विभाजित करते है ${{\lambda :1}}$ तो हमारे पास है 

$OB  =  \dfrac{(\lambda OC+OA)}{(\lambda +1)}$

${{5i - 2k  =  (\lambda (11i + 3j + 7k) + (i - 2j - 8k))/(\lambda  + 1)}}$

${{(\lambda  + 1)(5i - 2k)  =  11\lambda i + 3\lambda j + 7\lambda k + i - 2j - 8k}}$

${{5(\lambda  + 1)i - 2(\lambda  + 1)k  =  (11\lambda  + 1)i + (3\lambda  - 2)j + (7\lambda  - 8)k}}$ 

संबंधित घटकों को बराबर करने पर हमे यह मिलता है 

${{5(\lambda  + 1)  =  11\lambda  + 1}}$

${{5\lambda  + 5  =  11\lambda  + 1}}$

${{6\lambda   =  4}}$

${{\lambda   =  \dfrac{4}{6}  =  \dfrac{2}{3}}}$

इसलिए बिन्दु B अनुपाद मे AC को विभाजित करता है ${{2:3}}$

9. एक बिन्दु R की स्थिति वेक्टर को खोजे जो दो बिन्दुओ P और Q को मिलाने वाली रेखा को विभाजित करता है जिसकी वेक्टर ${{((2a) + b) , (a - 3b)}}$ बाहरी रूप से ${{1:2}}$ के अनुपद मे है। यह भी बताए कि P, रेखा खंड RQ का मध्य बिन्दु है। 

उत्तर: यह दिया गया है की OP = ${{2a  + b}}$ , OQ = ${{a  - 3b}}$

यह दिया गया है की बिन्दु R अनुपाद मे दो बिन्दु P और Q को मिलाकर एक रेखा खंड को विभाजित करता है ${{1:2}}$ फिर अनुभाग सूत्र का उपयोग करने पर हमे यह मिलता है 

$OR = \dfrac{(2(2a+b)-(a-3b))}{(2-1)}=\dfrac{(4a+2b-a+3b)}{1}=3a+5$

इसलिए बिन्दु R की स्थिति वेक्टर है ${{3a + 5}}$

RQ के मध्य बिन्दु की स्थिति वेक्टर = $\dfrac{(OQ + OR)}{2}$ 

${{ =  \dfrac{(a-3b)+(3a+5b)}{2}}}$

${{ =  2a + b}}$

${{ =  OP}}$ 

इसलिए P लाइन सेगमेंट का मध्य बिन्दु है RQ

10. समांतर चतुर्भुज के दो समीपवर्ती भाग ${{2i - 4j + 5k , i - 2j - 3k}}$ है। इकाई विकर्ण को इसके विकर्ण के संयंत्र खोजे। इसके अलावा इसके क्षेत्र का पता लगाए। 

उत्तर: समांतर चतुर्भुज के समीपवर्ती भुजाये दी गई है ${{a  =  2i - 4j + 5k , b  =  i - 2j - 3k}}$

फिर एक समांतर चतुर्भुज के विकर्ण द्वारा दिया जाता है ${{a + b}}$

${{a + b  =  (2 + 1)i + ( - 4 - 2)j + (5 - 3)k  =  3i - 6j + 2k}}$

इस प्रकार, विकर्ण के समांतर इकाई वेक्टर है 

$\dfrac{(a+b)}{|a+b|}=\dfrac{(3i - 6j + 2k)}{\sqrt {{{{3}}^2}{{ + ( - 6}}{{{)}}^{{2}}}{{ + }}{{{2}}^{{2}}}}}$

$=\dfrac{(3i - 6j + 2k)}{\sqrt {{{9 + 36 + 4}}}}$

$=\dfrac{3}{7}i-\dfrac{6}{7}j+\dfrac{2}{7}k$

समांतर चतुर्भुज ABCD का क्षेत्रफल = ${{|a \times b|}}$

${{ =  i(12 + 10) - j( - 6 - 5) + k( - 4 + 4)}}$

${{ =  22i + 11j  =  11(2i + j)}}$

${{|a \times b|  =  11}}\sqrt {\left( {{{{2}}^{{2}}}{{ + }}{{{1}}^{{2}}}} \right)} {{  =  11}}\sqrt {{5}}$ 

इसलिए समांतर चतुर्भुज का क्षेत्रफल ${{11}}\sqrt {{5}}$ वर्ग इकाई है। 

11. दिखाए की एक सदिश का कोसाइन अक्षों पर समान रूप से झुक होता है OX, OY, OZ कर रहे है ${{(}}\dfrac{1}{{\sqrt 3 }},\;\dfrac{1}{{\sqrt 3 }},\;\dfrac{1}{{\sqrt 3 }})$

उत्तर: आइए a वेक्टर कुल्हाड़ियों के समान रूप से झुक हुआ हो OX, OY, OZ कोण पर ${{\alpha }}$

फिर वेक्टर की दिशा कोसाइन है ${{cos\alpha  , cos\alpha  , cos\alpha }}$

अभी 

${{Co}}{{{s}}^{{2}}}{{\alpha  + Co}}{{{s}}^{{2}}}{{\alpha  + Co}}{{{s}}^{{2}}}{{\alpha   =  1}}$

${{3Co}}{{{s}}^{{2}}}{{\alpha   =  1}}$

${{Cos\alpha   =  (1/}}\sqrt {{3}} {{)}}$ 

इसलिए वेक्टर की दिशा कोसाइन जो कुल्हाड़ियों के लिए समान रूप से झुकी हुई है ${{(}}\dfrac{1}{{\sqrt 3 }}),\;(\dfrac{1}{{\sqrt 3 }}),\;(\dfrac{1}{{\sqrt 3 }})$

12. ${{a  = }}\;{{i + 4j + 2k , b  =  3i - 2j + 7k ,}}\;{{c}}\;{{ = }}\,{{2i - j + 4k}}$ एक वेक्टर डी खोजे जो a और b दोनों के लिए लम्बवत है और ${{c}}{{. d  =  15}}$

उत्तर: चलो ${{d  =  }}{{{d}}_1}{{i + }}{{{d}}_2}{{j + }}{{{d}}_3}{{k}}$

चूंकि d, a और b दोनों के लिए लम्बवत है, हमारे पास है 

${{d}}{{.a  =  0}}$

${{{d}}_1}{{ + 4}}{{{d}}_2}{{ + 2}}{{{d}}_3}{{  =  0}}$ ........(i)

तथा ${{d}}{{.b  =  0}}$

${{3}}{{{d}}_1}{{ - 2}}{{{d}}_2}{{ + 7}}{{{d}}_3}{{  =  0}}$ ........(ii)

इसके अलावा यह दिया गया है की ${{c}}{{.d  =  14}}$

${{2}}{{{d}}_1}{{ - }}{{{d}}_2}{{ + 4}}{{{d}}_3}{{  =  15}}$ ........(iii)

हल करने पर (i), (ii), (iii) हमे मिलता है 

${{{d}}_1}{{  =  \dfrac{160}{3} , }}{{{d}}_2}{{  =  \dfrac{-5}{3} , }}{{{d}}_3}{{  =  \dfrac{-70}{3}}}$

${{d  =  (\dfrac{160}{3})i - (\dfrac{5}{3})j - (\dfrac{70}{3})}}$

${{ =  (\dfrac{1}{3})(160i - 5j - 70k)}}$ 

इसलिए आवश्यक वेक्टर है  ${{(\dfrac{1}{3})(160i - 5j - 70k)}}$

13. वेक्टर ${{2i + 4j - 5k , \lambda i + 2j + 3k}}$ के योग के साथ एक वेक्टर के साथ वेक्टर ${{i  + j  + k}}$ का स्केलर उत्पाद एक के बराबर है। ${{\lambda }}$ का मान ज्ञात कीजिए। 

उत्तर: $(2 \hat{i}+4 \hat{j}-5 \hat{k})+(\lambda \hat{i}+2 \hat{j}+3 \hat{k})$

$=(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}$

इसलिए यूनिट वेक्टर साथ$(2 \hat{i}+4 \hat{j}-5 \hat{k})+(\lambda \hat{i}+2 \hat{j}+3 \hat{k})$ दिया है : $\dfrac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{(2+\lambda)^{2}+6^{2}+(-2)^{2}}}=\dfrac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{4+4 \lambda+\lambda^{2}+36+4}}=\dfrac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{\lambda^{2}+4 \lambda+44}}$

का स्केलर उत्पाद $(\hat{i}+\hat{j}+\hat{k})$ इस इकाई के साथ वेक्टर एक है। 

$\Rightarrow(\hat{i}+\hat{j}+\hat{k}) \cdot \dfrac{(2+\lambda) \hat{i}+6 \hat{j}-2 \hat{k}}{\sqrt{\lambda^{2}+4 \lambda+44}}=1$

$\Rightarrow \dfrac{(2+\lambda)+6-2}{\sqrt{\lambda^{2}+4 \lambda+44}}=1$

$\Rightarrow \sqrt{\lambda^{2}+4 \lambda+44}=\lambda+6$

$\Rightarrow \lambda^{2}+4 \lambda+44=(\lambda+6)^{2}$

$\Rightarrow \lambda^{2}+4 \lambda+44=\lambda^{2}+12 \lambda+36$

$\Rightarrow 8 \lambda=8$

$\Rightarrow \lambda=1$

$\lambda$ =1 .

इसलिए ${{\lambda }}$ का मान ${{1}}$ है। 

14. यदि a, b, c समान रूप से परिणाम के लम्बवत वेक्टर है तो दिखते है की वेक्टर ${{a + b + c}}$ समान रूप से a, b, c के समान है। 

उत्तर: जबसे a, b, c परस्पर लम्बवत वेक्टर है हमारे पास है 

${{a}}{{.b  =  b}}{{.c  =  c}}{{.a  =  0}}$

यह दिया जाता है कि:

${{|a|  =  |b|  =  |c|}}$

आइए वेक्टर को ${{a + b + c}}$ के कोणों पर a, b, c के रूप मे झुकाए ${{{\theta }}_1}{{, }}{{{\theta }}_2}{{, }}{{{\theta }}_3}$ क्रमश: 

तो हमारे पास है: 

${{Cos }}{{{\theta }}_1}{{  =  \dfrac{((a + b + c) \times a)}{(|a + b + c| |a|)}  =  }}$$\dfrac{(a \times a + b \times a + c.a)}{|a + b + c| |a|}$${{ =  \dfrac{|a|}{(|a + b + c|)}}}$

${{Cos }}{{{\theta }}_{{2}}}{{  =  \dfrac{((a + b + c) \times b)}{(|a + b + c| |b|)}  =  \dfrac{(a \times b + b \times b + c \times b)}{|a + b + c| |b| } = \dfrac{|b|}{(|a + b + c|}}}$

${{Cos}}{{{\theta }}_3}{{  =  \dfrac{((a + b + c) \times c)}{(|a + b + c| |c|) } =  }}$${{\dfrac{(a \times c + b \times c + c \times c)}{|a + b + c| |c|}}}$ = ${{\dfrac{|c|}{(|a + b + c|)}}}$

अभी ${{|a|  =  |b|  =  |c| , Cos}}{{{\theta }}_1}{{  =  Cos}}{{{\theta }}_2}{{  =  Cos}}{{{\theta }}_3}$

${{{\theta }}_1}{{  =  }}{{{\theta }}_2}{{  =  }}{{{\theta }}_3}$

इसलिए वेक्टर ${{a + b + c}}$ समान रूप से ${{a , b , c}}$ के लिए झुक है।  

15. सिद्ध कीजिए की ${{(a + b) \times (a + b)  =  |a}}{{{|}}^{{2}}}{{ + |b}}{{{|}}^{{2}}}$ इफफ यदि a, b लम्बवत है तो ${{a}} \ne {{0 , b}} \ne {{0}}$

उत्तर:   ${{(a + b) \times (a + b)  =  |a}}{{{|}}^{{2}}}{{ + |b}}{{{|}}^{{2}}}$

${{a \times a + a \times b + b \times a + b \times b  =  |a}}{{{|}}^{{2}}}{{ + |b}}{{{|}}^{{2}}}$

${{|a}}{{{|}}^{{2}}}{{ + 2a \times b + |b}}{{{|}}^{{2}}}{{  =  |a}}{{{|}}^{{2}}}{{ + |b}}{{{|}}^{{2}}}$

${{2a \times b  =  0}}$

${{a \times b  =  0}}$ 

${{a , b}}$ लम्बवत है। 

16. यदि ${{\theta }}$ दो वेक्टर a और b के बीच का कोण है तो ${{a,b}} \geqslant 0$ केवल जब 

(a) ${{0 < \theta  < (\pi /2)}}$

(b) ${{0}} \leqslant {{\theta }} \leqslant {{(\pi /2)}}$

(c) ${{0 < \theta  < \pi }}$

(d) ${{0}} \leqslant {{\theta }} \leqslant {{\pi }}$

उत्तर: बता दे की ${{\theta }}$ दो वेक्टर के बीच का कोण है a तथा b

फिर, सामान्यता के नुकसान के बिना a, b गैर शून्य वेक्टर है ताकि ${{|a| , |b|}}$ सकारात्मक है 

यह जाना जाता है कि ${{a \times b  =  |a| |b| cos\theta }}$

${{a \times b}} \geqslant {{0}}$

${{|a| |b| cos\theta }} \geqslant {{0}}$

${{cos\theta }} \geqslant {{0}}$

${{0}} \leqslant {{\theta }} \leqslant {{(\pi /2)}}$ 

इसलिए ${{a \times b}} \geqslant {{0}}$ कब ${{0}} \leqslant {{\theta }} \leqslant {{(\pi /2)}}$

अतः सही विकल्प (b) है। 

17. बता दे की a और b फ़ो यूनिट वेक्टर है और ${{\theta }}$ उनके बीच का कोण है तो ${{a  + b}}$ एक इकाई वेक्टर है अगर 

(a) ${{\theta   =  (\dfrac{\pi} {4})}}$

(b) ${{\theta   =  (\dfrac{\pi} {3})}}$

(c) ${{\theta   =  (\dfrac{\pi} {2})}}$

(d) ${{\theta   =  (\dfrac{2\pi} {3})}}$

उत्तर: बता दे की a और b फ़ो यूनिट वेक्टर है और ${{\theta }}$ उनके बीच का कोण है

फिर ${{|a|  =  |b|  =  1}}$

अब ${{|a + b|}}$ एक इकाई वेक्टर है यदि ${{|a + b|  =  1}}$

${{|a + b|  =  1}}$

${{{(a + b)}}^{{2}}}{{  =  1}}$

${{(a + b) \times (a + b)  =  1}}$

${{a \times a + a \times b + b \times a + b \times b  =  1}}$

${{|a}}{{{|}}^{{2}}}{{ + 2a \times b + |b}}{{{|}}^{{2}}}{{  =  1}}$

${{{1}}^{{2}}}{{ + 2|a| |b}}\mid {{cos\theta  + }}{{{1}}^{{2}}}{{  =  1}}$

${{1 + 2}}{{.1}}{{.1cos\theta  + 1  =  1}}$

${{cos\theta   =  ( \dfrac{- 1}{2})}}$

${{\theta   =  (\dfrac{2\pi} {3})}}$ 

इसलिए ${{a + b}}$ एक इकाई वेक्टर है यदि ${{\theta   =  (\dfrac{2\pi} {3})}}$

अतः सही विकल्प (d) है। 

18. ${{i(j \times k) + j}}{{.(i \times k) + k \times (i \times j)}}$ का मान है। 

(a) ${{0}}$

(b) ${{ - 1}}$

(c) ${{1}}$

(d) ${{3}}$

उत्तर: ${{i(j \times k) + j}}{{.(i \times k) + k \times (i \times j)}}$

${{ = }}\;{{i}}{{.i + j( - j) + k}}{{.k}}$

${{ =  1 - j}}{{.j + 1}}$

${{ =  1 - 1 + 1}}$

${{ =  1 }}$ 

अतः सही विकल्प (c) है। 

19. यदि ${{\theta }}$ किसी भी दो वेक्टर a और b के बीच का कोण है तो ${{|a|}}{{|b|  =  |a \times b}}\mid $ जब ${{\theta }}$ के बराबर है। 

(a) ${{0}}$

(b) ${{(\dfrac{\pi} {4})}}$

(c) ${{(\dfrac{\pi} {2})}}$

(d) ${{\pi }}$

उत्तर: बता दे कि ${{\theta }}$ दो वेक्टर a और b के बीच का कोण है। 

फिर, सामान्यता के नुकसान के बिना a, b गैर शून्य वेक्टर है 

इसलिए ${{|a}}\mid  , {{|b|}}$ सकारात्मक है 

${{|a \times b|  =  |a \times b|}}$

${{|a| |b| cos\theta   =  |a| |b| sin\theta }}$

${{Cos\theta   =  Sin\theta }}$

${{Tan\theta   =  1}}$

${{\theta   =  (\dfrac{\pi} {4})}}$ 

इसलिए $\mid {{a}}{{b|  =  |a \times b}}\mid$ जब ${{(\dfrac{\pi} {4})}}$ के बराबर हो। 

अतः सही विकल्प (b) है।  

NCERT Solutions  for Class 12 Maths Chapter 10 Vector Algebra In Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 12 Maths Chapter 10 solution Hindi medium is created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 12 Maths Chapter 10 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 12 Maths Chapter 10 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 12 Maths Vector Algebra solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that. 

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 12 Maths Vector Algebra in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 12 can download these solutions at any time as per their convenience for self-study purpose. 

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 12 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examination.