NCERT Solutions for Class 9 Maths Chapter 7 - In Hindi

प्रश्नावली 7.1

1. चतुर्भुज \[\mathbf{ABCD}\] में, \[\mathbf{AC}\text{ }=\text{ }\mathbf{AD}\] है और \[\mathbf{AB}\] कोण \[\mathbf{A}\] को समद्विभाजित करता है। दर्शाइए कि \[\mathbf{\Delta ABC}\cong \mathbf{\Delta ABD}\] है।

\[\mathbf{BC}\] और \[\mathbf{BD}\] के बारे में आप क्या कह सकते हैं?

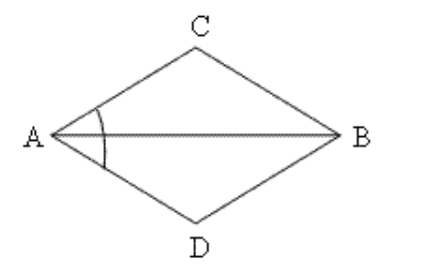
उत्तर: \[\Delta ACB\text{ , }\Delta ABD\] में

\[AC\text{ }=\text{ }AD\]

\[\angle CAB\text{ }=\angle DAB\text{ }(\angle CAD\] को \[AB\] समद्विभाजित कर रहा है)

\[AB\text{ }=\text{ }AB\] (साझा भुजा)

इसलिए, \[SAS\] स्वयंसिद्धि के अनुसार:

\[\Delta ACB\cong \Delta ABD\] सिद्ध हुआ

2. \[\mathbf{ABCD}\] एक चतुर्भुज है, जिसमें \[\mathbf{AD}\text{ }=\text{ }\mathbf{BC}\] और \[\angle \mathbf{DAB}\text{ }=\angle \mathbf{CBA}\] है। सिद्ध कीजिए कि

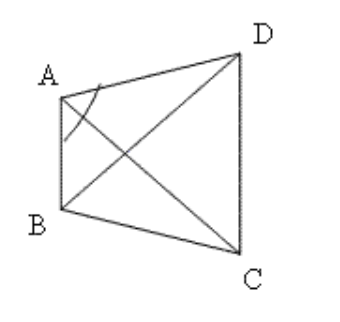
1. $ \Delta ABD\cong \Delta BAC $

2. $ BD = AC $

3. $\angle ABD =\angle BAC $

उत्तर: \[\Delta ABD\] और \[\Delta BAC\] में

\[AD\text{ }=\text{ }BC\]

\[AB\text{ }=\text{ }AB\] (साझा भुजा)

\[\angle BAD\text{ }=\angle ABC\]

इसलिए \[SAS\] नियम के अनुसार, \[\Delta ABD\] समानुपाती \[\Delta BAC\] सिद्ध हुआ।

चूँकि \[\Delta ABD\cong \Delta BAC\]

इसलिए, \[BD\text{ }=\text{ }AC\]

(त्रिभुजों की तीसरी संगत भुजाएँ)

सर्वांगसम त्रिभुजों के हर संगत कोण बराबर होते हैं।

इसलिए, \[\angle BAD\text{ }=\angle ABC\] सिद्ध हुआ।

3. एक रेखाखंड \[\mathbf{AB}\] पर \[\mathbf{AD}\] और \[\mathbf{BC}\] दो बराबर लंब रेखाखंड हैं। दर्शाइए कि रेखाखंड \[\mathbf{CD}\], रेखाखंड \[\mathbf{AB}\] को समद्विभाजित करता है।

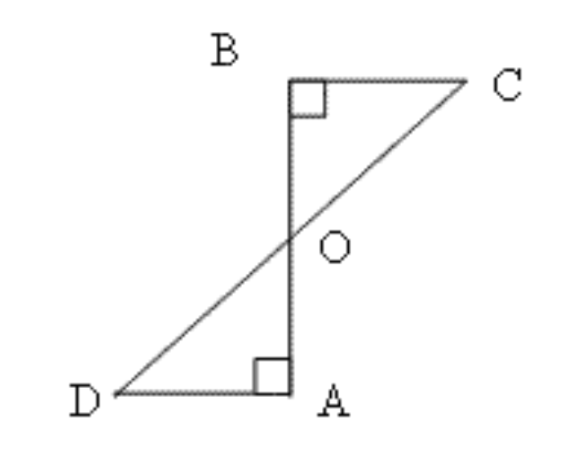
उत्तर: \[\Delta BOC\] और \[\Delta AOD\] में

\[BC\text{ }=\text{ }AD\] (दिया गया है)

\[\angle CBO\text{ }=\angle DAO\] (समकोण)

\[\angle BOC\text{ }=\angle AOD\] (सम्मुख कोण)

इसलिए \[ASA\] नियम के अनुसार,

\[\Delta BOC\cong \Delta AOD\]

या\[,\text{ }BO\text{ }=\text{ }AO\]

और यह सिद्ध हुआ कि \[AB\] का समद्विभाजक \[CD\] है।

4. \[\mathbf{l}\] और \[\mathbf{m}\] दो समांतर रेखाएँ है जिन्हें समांतर रेखाओं \[\mathbf{p}\] और \[\mathbf{q}\] का एक अन्य युग्म प्रतिच्छेदित करता है। दर्शाइए कि ΔABC ≅ ΔCDA है।

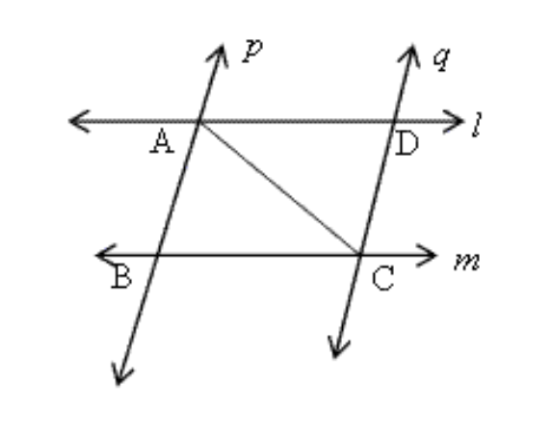
उत्तर: \[\Delta ABC\] और \[\Delta CDA\] में

\[AB\text{ }=\text{ }CD\] (\[l~\] और \[m\] समांतर हैं)

\[AD\text{ }=\text{ }BC\text{ }(AB\] और \[CD\] समांतर हैं)

\[\angle ABC\text{ }=\angle DCm\] (तिर्यक रेखा \[BC\] के एक ही ओर के कोण)

\[\angle DCm\text{ }=\angle ADC\]

\[\angle ABC\text{ } = \angle ADC\]

इसलिए, \[SAS\] नियम के अनुसार \[\Delta ABC\cong \Delta CDA\]

5.  रेखा \[\mathbf{l}\] कोण \[\mathbf{A}\] को समद्विभाजित करती है और \[\mathbf{B}\] रेखा \[\mathbf{l}\] पर स्थित कोई बिंदु है। \[\mathbf{BP}\] और \[\mathbf{BQ}\] कोण \[\mathbf{A}\] की भुजाओं पर \[\mathbf{B}\] से डाले गए लम्ब हैं। दर्शाइए कि

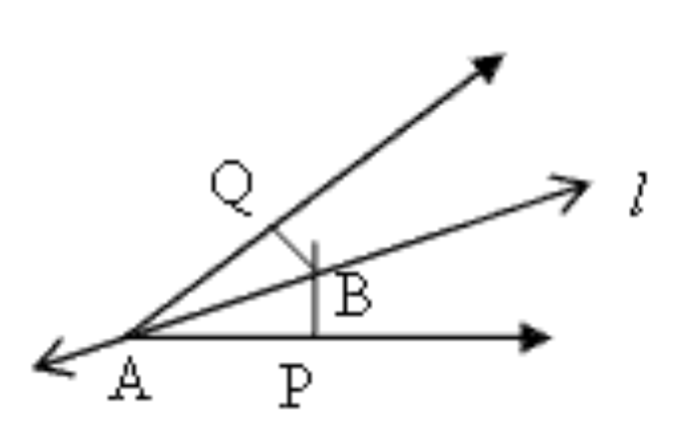
1. \[\mathbf{\Delta APB}\cong \mathbf{\Delta AQB}\]

2. \[\mathbf{BP}\text{ }=\text{ }\mathbf{BQ}\] है, अर्थात बिंदु \[B\] कोण की भुजाओं से समदूरस्थ है।

उत्तर: \[\Delta APB\] और \[\Delta AQB\] में

\[AB\text{ }=\text{ }AB\] (साझा भुजा)

\[\angle PAB\text{ }=\angle QAB\] \[(\angle QAP\] को \[AB\] समद्विभाजित करता है)

\[\angle AQB\text{ }=\angle APB\] (समकोण)

इसलिए\[,\text{ }ASA\] नियम के अनुसार, \[\Delta APB\cong \Delta AQB\]

और \[BQ\text{ }=\text{ }BP\]

6. दी गई आकृति में, \[\mathbf{AC}\text{ }=\text{ }\mathbf{AE},\text{ }\mathbf{AB}\text{ }=\text{ }\mathbf{AD}\] और \[\angle \mathbf{BAD}\text{ }=\angle \mathbf{EAC}\] है। दर्शाइए कि \[\mathbf{BC}\text{ }=\text{ }\mathbf{DE}\] है।

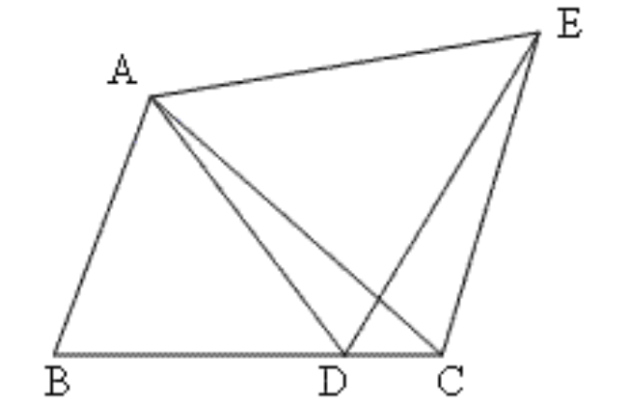
उत्तर: \[\Delta ABC\] और \[\Delta ADE\] में

\[AB=AD\] (दिया गया है)

\[AC\text{ }=\text{ }AE\] (दिया गया है)

चूँकि \[\angle BAD\text{ }=\angle EAC\]

इसलिए, \[\angle BAD\text{ }+\angle DAC\text{ }=\angle EAC\text{ }+\angle DAC\]

या, \[\angle BAC\text{ }=\angle DAE\]

इसलिए, \[SAS\] नियम के अनुसार \[\Delta ABC\cong \Delta ADE\]

या, \[BC\text{ }=\text{ }DE\] सिद्ध हुआ

7. \[\mathbf{AB}\] एक रेखाखंड है और \[\mathbf{P}\] इसका मध्य बिंदु है। \[\mathbf{D}\] और \[\mathbf{E}\] रेखाखंड \[\mathbf{AB}\] के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि \[\angle \mathbf{BAD}\text{ }=\angle \mathbf{ABE}\] और \[\angle \mathbf{EPA}\text{ }=\angle \mathbf{DPB}\] है। दर्शाइए कि

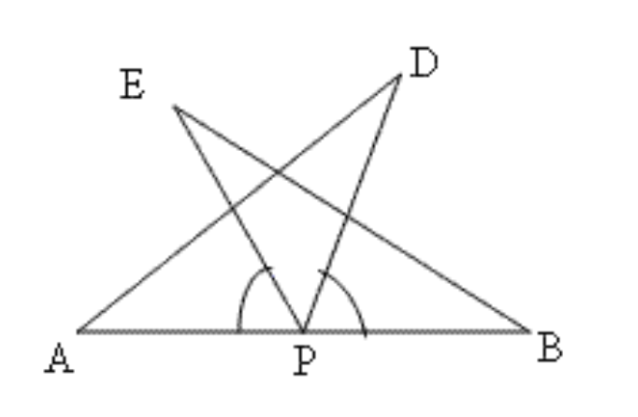
1. \[\mathbf{\Delta DAP}\cong \mathbf{\Delta EBP}\]

2. \[\mathbf{AD}\text{ }=\text{ }\mathbf{BE}\]

उत्तर: \[\Delta DAP\] और \[\Delta EBP\] में

\[\angle BAD\text{ }=\angle ABE\] (दिया गया है)

\[\angle EPA\text{ }=\angle DPB\] (दिया गया है)

इसलिए, \[\angle EPA\text{ }+\angle EPD=\angle DPB\text{ }+\angle EPD\]

या, \[\angle DPA\text{ }=\angle EPB\]

\[AP\text{ }=\text{ }PB\] (\[AB\] का मध्यबिंदु \[P\] है)

इसलिए, \[ASA\] नियम के अनुसार, \[\Delta DAP\cong \Delta EBP\]

या\[,\text{ }AD\text{ }=\text{ }BE\]

8. एक समकोण त्रिभुज \[\mathbf{ABC}\] में, जिसमें कोण \[\mathbf{C}\] समकोण है, \[\mathbf{M}\] कर्ण \[\mathbf{AB}\] का मध्य बिंदु है। \[\mathbf{C}\] को \[\mathbf{M}\] से मिलाकर D तक इस प्रकार बढ़ाया गया है कि \[\mathbf{DM}\text{ }=\text{ }\mathbf{CM}\] है। बिंदु \[\mathbf{D}\] को बिंदु \[\mathbf{B}\] से मिला दिया जाता है। दर्शाइए कि

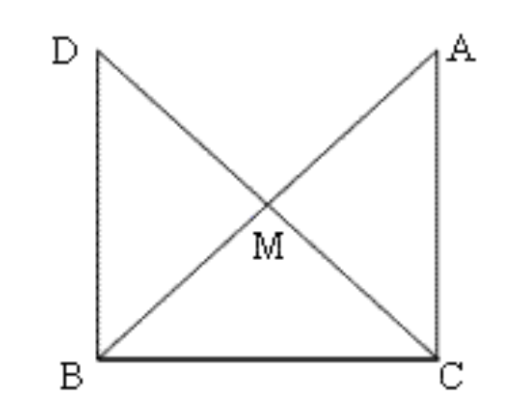
1.  \[\mathbf{\Delta AMC}\cong \mathbf{\Delta BMD}\]

2. \[\angle \mathbf{DBC}\] एक समकोण है।

3. \[\mathbf{\Delta DBC}\cong \mathbf{\Delta ACB}\]

4. \[\mathbf{CM}=\frac{1}{2}\mathbf{AB}\]

उत्तर: \[~\Delta AMC\] और \[\Delta BMD\] में

\[BM\text{ }=\text{ }AM\] (\[M\] मध्य बिंदु है)

\[DM\text{ }=\text{ }CM\] (दिया गया है)

\[\angle DMB\text{ }=\angle AMC\] (सम्मुख कोण)

इसलिए, \[\Delta AMC\cong \Delta BMD\]

इसलिए, \[DB\text{ }=\text{ }AC\]

\[\angle DBA\text{ }=\angle BAC\]

इसलिए, \[DB||AC\] (एकांतर कोण बराबर हैं)

इसलिए, \[\angle BDC\text{ }=\angle ACB\text{ }=\]समकोण

(तिर्यक रेखा के एक ही ओर के अंत:कोण पूरक होते हैं।)

\[\Delta DBC\] और \[\Delta ACB\] में

\[DB\text{ }=\text{ }AC\] (पहले सिद्ध हो चुका है)

\[BC\text{ }=\text{ }BC\] (साझा भुजा)

∠ \[BDC\text{ }=\angle ACB\] (पहले सिद्ध हो चुका है)

इसलिए, \[\Delta DBC\cong \Delta ACB\]

इसलिए, \[AB\text{ }=\text{ }DC\]

इसलिए, \[AM\text{ }=\text{ }BM\text{ }=\text{ }CM\text{ }=\text{ }DM\]

इसलिए, \[CM=\frac{1}{2}AB\]

प्रश्नावली 7.2

1. एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। A और O को जोड़िए। दर्शाइए कि

\[\mathbf{OB}\text{ }=\text{ }\mathbf{OC}\]

\[\mathbf{AO}\] कोण \[\mathbf{A}\] को समद्विभाजित करता है।

उत्तर: \[\Delta OBC\] में

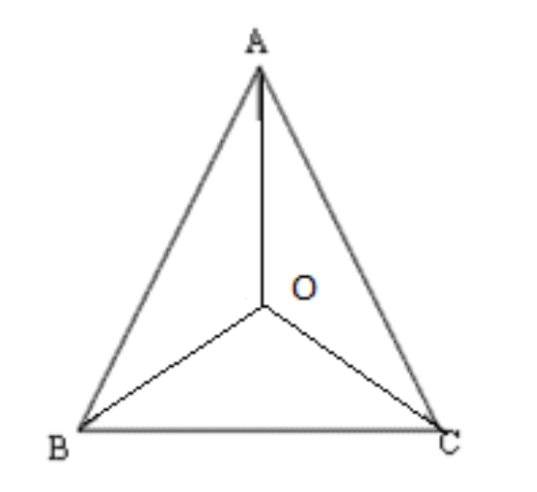
\[\angle OBC\text{ }=\angle OCA\] (ये कोण \[B\] और \[C\] के आधे हैं)

इसलिए, \[OB\text{ }=\text{ }OC\] (समान कोणों के सामने वाली भुजाएँ)

\[\Delta AOB\] और \[\Delta AOC\] में

\[AB\text{ }=\text{ }AC\] (दिया गया है)

\[OB\text{ }=\text{ }OC\] (पहले सिद्ध हो चुका है)

\[\angle ABO\text{ }=\angle ACO\] (ये कोण \[B\] और \[C\] के आधे हैं)

इसलिए, \[\Delta AOB\cong \Delta AOC\] (\[SAS\] नियम)

इसलिए, \[\angle BAO\text{ }=\angle CAO\]

इसका मतलब है \[\angle A\] को समद्विभाजित करता है।

2. \[\mathbf{\Delta ABC}\] में \[\mathbf{AD}\] भुजा \[\mathbf{BC}\] का लम्ब समद्विभाजक है। दर्शाइए कि \[\mathbf{\Delta ABC}\] एक समद्विबाहु त्रिभुज है, जिसमें \[\mathbf{AB}\text{ }=\text{ }\mathbf{AC}\] है।

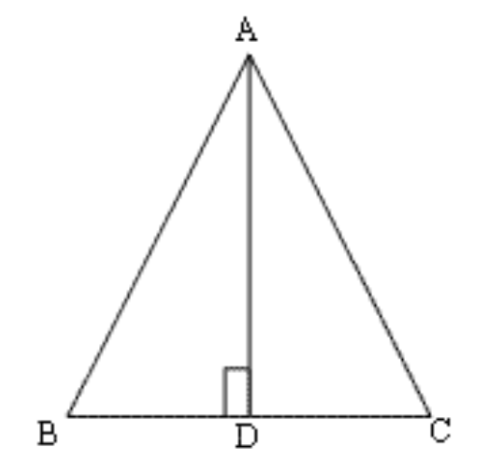
उत्तर: \[\Delta ABD\] में \[\Delta ACD\] में

\[AD\text{ }=\text{ }AD\] (साझा भुजा)

\[BD\text{ }=\text{ }CD\] (दिया गया है)

\[\angle ADB\text{ }=\angle ADC\] (समकोण)

इसलिए, \[\Delta ABD\cong \Delta ACD\]

इसलिए\[,\text{ }AB\text{ }=\text{ }AC\]

यह सिद्ध हुआ कि \[\Delta ABC\] एक समद्विबाहु त्रिभुज है।

3. \[\mathbf{ABC}\] एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमश: शीर्षलम्ब \[\mathbf{BE}\] और \[\mathbf{CF}\] खींचे गए हैं। दर्शाइए कि ये शीर्षलम्ब बराबर हैं।

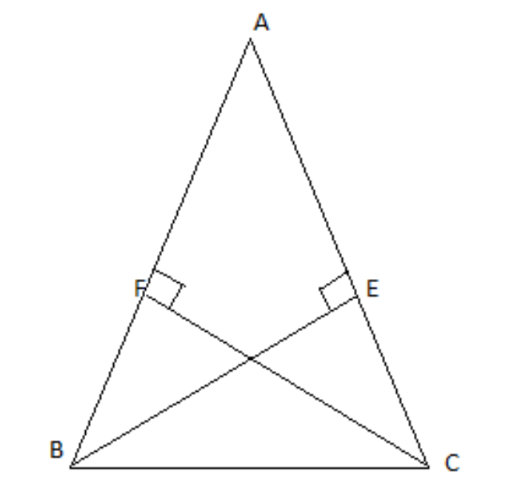
उत्तर: \[\Delta ABE\] और \[\Delta ACF\] में

\[AB\text{ }=\text{ }AC\] (दिया गया है)

\[\angle BAE\text{ }=\angle CAF\] (साझा कोण)

\[\angle CFA\text{ }=\angle BEA\] (समकोण)

इसलिए, \[\Delta ABE\cong \Delta ACF\text{ }(ASA\] नियम)

इसलिए, \[BE\text{ }=\text{ }CF\]

4. \[\mathbf{ABC}\] एक त्रिभुज है जिसमें \[\mathbf{AC}\] और \[~\mathbf{AB}\] पर खींचे गए शीर्षलम्ब \[\mathbf{BE}\] और \[\mathbf{CF}\] बराबर हैं। दर्शाइए कि

1. \[\mathbf{\Delta ABE}\cong \mathbf{\Delta ACF}\]

2. \[\mathbf{AB}\text{ }=\text{ }\mathbf{AC}\], अर्थात \[\mathbf{\Delta ABC}\] एक समद्विबाहु त्रिभुज है।

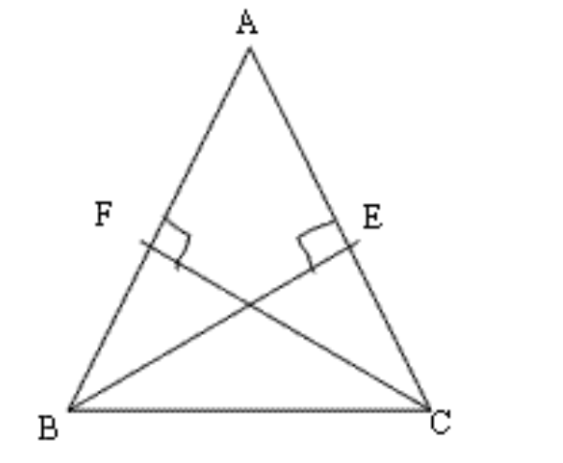
उत्तर: दिया है ABC एक त्रिभुज है जिसमे शीर्षलम्ब \[\mathbf{BE}\] और \[\mathbf{CF}\] बराबर

\[\Delta ABE\] और \[\Delta ACF\] में

\[BE=CF\]

\[\angle AEB=\angle AFC\](\[{{90}^{0}}\] प्रत्येक)

\[\angle A=\angle A\](उभयनिष्ठ )

ASA सर्वांगसम नियम के उपयोग से,

\[\Delta ABE\cong \Delta ACF\]

\[\left( ii \right)AB=AC(CPCT\] से,)

इसीलिए \[,ABC\] एक समद्विबाहु त्रिभुज है।

5. \[\text{ }\mathbf{ABC}\] और \[\mathbf{DBC}\] समान आधार \[\mathbf{BC}\] पर स्थित दो समद्विबाहु त्रिभुज हैं। दर्शाइए कि \[\angle \mathbf{ABD}\text{ }=\angle \mathbf{ACD}\] है।

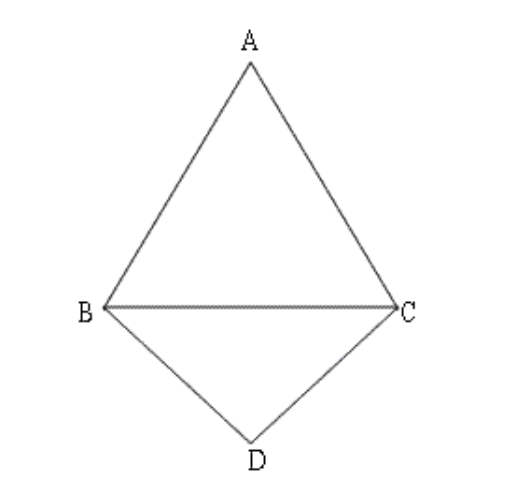
उत्तर: \[\angle ABC\text{ }=\angle ACB\]

\[\angle DBC\text{ }=\angle DCB\]

इसलिए\[,\angle ABC\text{ }+\angle DBC\text{ }=\angle ACB\text{ }+\angle DCB\]

या, \[\angle ABD\text{ }=\angle ACD\]

6. \[\mathbf{ABC}\] एक समद्विबाहु त्रिभुज है, जिसमें \[\mathbf{AB}\text{ }=\text{ }\mathbf{AC}\] है। भुजा \[\mathbf{BA}\] बिंदु \[\mathbf{D}\] तक इस प्रकार बढ़ाई गई है कि \[\mathbf{AD}\text{ }=\text{ }\mathbf{AB}\] है। दर्शाइए कि \[\angle \mathbf{BCD}\] एक समकोण है।

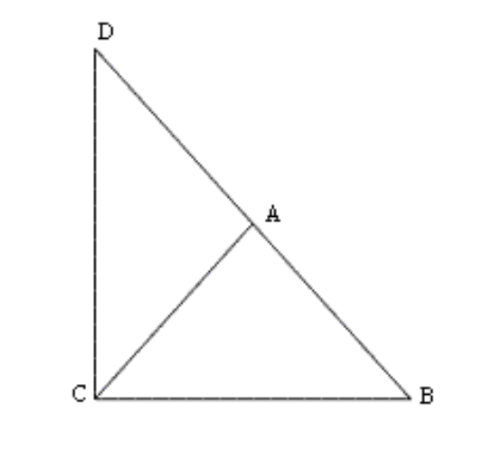
उत्तर: \[\Delta ADC\] और \[\Delta ABC\] में

  $AD\text{ }=\text{ }AB$

  $ AB\text{ }=\text{ }AC $

  $\angle ACB\text{ }=\angle ABC  $

  $\therefore AC\text{ }=\text{ }AD $

   $\angle ACD\text{ }=\angle ADC $

\[\Delta ABC\] में, \[\angle ACB\text{ }+\angle ABC\text{ }+\angle CAB\text{ }=\text{ }180{}^\circ \]

या, \[\angle CAB\text{ }=\text{ }180{}^\circ -2\angle ACB\text{ }............\left( 1 \right)\]

इसी तरह, \[\Delta ADC\] में

\[\angle DAC\text{ }=\text{ }180{}^\circ \text{ }-\text{ }2\angle ACD...............\left( 2 \right)\]

चूँकि \[BD\] एक सरल रेखा है, इसलिए \[\angle CAB\text{ }+\angle DAC=180{}^\circ \]

इसलिए, समीकरण \[(1)\]और \[(2)\]को जोड़ने पर,

\[180{}^\circ \text{ }=\text{ }360{}^\circ \text{ }-\text{ }2\angle ACB\text{ }-\text{ }2\angle ACD\]’

या\[,\text{ }180{}^\circ \text{ }=\text{ }360{}^\circ \text{ }-\text{ }2(\angle ACB\text{ }+\angle ACD)\]

या, \[2(\angle ACB\text{ }+\angle ACD)\text{ }=\text{ }180{}^\circ \]

या, \[\angle ACB\text{ }+\angle ACD\text{ }=\angle BCD\text{ }=\text{ }90{}^\circ \]

7. \[\mathbf{ABC}\] एक समकोण त्रिभुज है, जिसमें \[\angle \mathbf{A}\text{ }=\text{ }\mathbf{90}{}^\circ \]और AB = AC  है। \[\angle \mathbf{B}\] और \[\angle \mathbf{C}\] ज्ञात कीजिए।

उत्तर: यदि \[AB\text{ }=\text{ }AC\] इन भुजाओं के सामने के कोण बराबर होंगे। आप जानते हैं कि त्रिभुज के तीनों कोणों का योग 180° होता है।

इसलिए, \[\angle A\text{ }+\angle B\text{ }+\angle C\text{ }=\text{ }180{}^\circ \]

या, \[90{}^\circ \text{ }+\angle B\text{ }+\angle C\text{ }=\text{ }180{}^\circ \]

या, \[\angle B\text{ }+\angle C\text{ }=\text{ }180{}^\circ \text{ }-\text{ }90{}^\circ \text{ }=\text{ }90{}^\circ \]

चूँकि AB = AC  

या, \[\angle B\text{ }=\angle C\text{ }=\text{ }45{}^\circ \]

8. दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण \[\mathbf{60}{}^\circ \]होता है।

उत्तर: हम जानते हैं कि किसी भी त्रिभुज में समान भुजाओं के सामने वाले कोण समान होते हैं। इसलिए समबाहु त्रिभुज की हर भुजा के सामने के कोण बराबर होंगे। इसलिए हर कोण का मान \[180{}^\circ \]का \[\frac{1}{3}\]भाग होगा, यानि \[60{}^\circ \] होगा।

प्रश्नावली 7.3

1. \[\text{ }\mathbf{\Delta ABD}\] और \[\mathbf{\Delta ACD}\] एक ही आधार पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि और भुजा के एक ही ओर स्थित हैं। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि

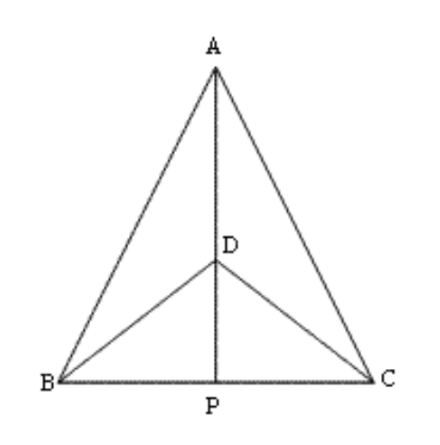
1. ΔABD ≅ ΔACD

2. ΔABP ≅ ΔACP

3. \[AP\] कोण \[A\] और कोण \[D\] दोनों को समद्विभाजित करता है।

4. \[AP\] रेखाखंड \[BC\] का लम्ब समद्विभाजक है।

उत्तर: \[\Delta ABD\] और \[\Delta ACD\] में

$AB\text{ }=\text{ }AC $

$ BD\text{ }=\text{ }CD $

 $ AD\text{ }=\text{ }AD  $

इसलिए, \[\Delta ABD\cong \Delta ACD\] \[(SSS\] नियम)

\[\Delta ABP\] और \[\Delta ACP\] में

  $ AB\text{ }=\text{ }AC $

  $ AP\text{ }=\text{ }AP $

\[\angle ABP\text{ }=\angle ACP\] (समान भुजाओं के सामने के कोण)

इसलिए, \[\Delta ABP\cong \Delta CP\] (\[SAS\] नियम)

चूँकि \[\Delta ABP\cong \Delta ACP\]

इसलिए, \[\angle BAP\text{ }=\angle CAP\]

इसलिए, \[\angle BAC\] को \[AP\] समद्विभाजित करता है।

इसी तरह, \[\Delta BDP\] और \[\Delta CDP\] सर्वांगसम सिद्ध किया जा सकता है और फिर यह भी सिद्ध किया जा सकता है कि \[\angle BDC\] को \[AP\] समद्विभाजित करता है।

2. \[\mathbf{AD}\] एक समद्विबाहु त्रिभुज \[\mathbf{ABC}\] का एक शीर्षलम्ब है, जिसमें \[\mathbf{AB}\text{ }=\text{ }\mathbf{AC}\] है। दर्शाइए कि

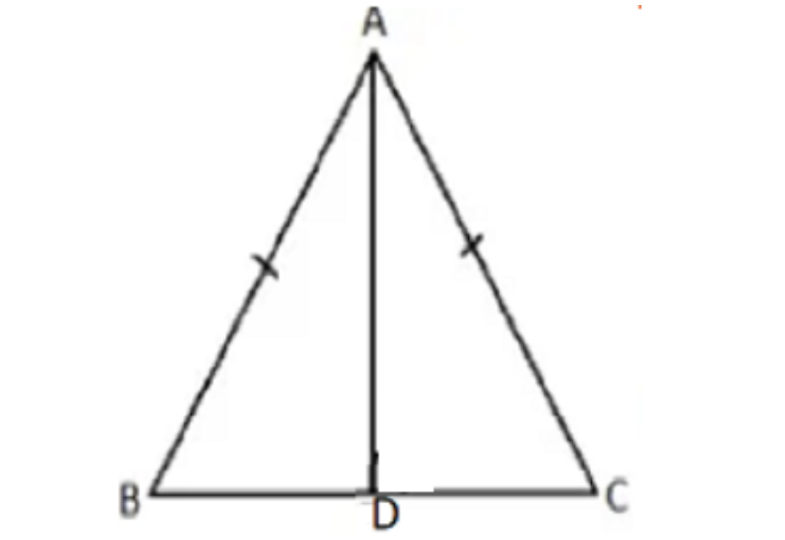
1. \[\mathbf{AD}\] रेखाखंड \[\mathbf{BC}\] को समद्विभाजित करता है।

2. \[\mathbf{AD}\] कोण \[\mathbf{A}\] को समद्विभाजित करता है।

उत्तर: \[\mathbf{AD}\] एक समद्विबाहु त्रिभुज \[\mathbf{ABC}\] का एक शीर्षलम्ब है,जिसमे AB=AC है।

\[\Delta ABD\]और \[\Delta ACD\] मे ,

\[AB=AC\] (दिया है )

\[AD=AD\] (उभयनिष्ठ भुजा)

\[\angle ABD=\angle ACD\]

SAS सर्वांगसम नियम से,

\[\therefore \Delta BDP ≅ \Delta CDP\]

अतः \[BD=CD..........(i)\text{ }(CPCT\] नियम से )

\[\angle BAD=\angle CAD..........(ii)\] 

समीकरण (i) से सिद्ध हुआ कि \[AD\] रेखाखण्ड \[BC\] को समद्विभाजित करता है।और समीकरण (ii) से यह सिद्ध हुआ कि \[AD\] कोण \[A\] को समद्विभाजित करता है।

3. एक त्रिभुज \[\mathbf{ABC}\] की दो भुजाएँ \[\mathbf{AB}\] और \[\mathbf{BC}\] तथा माध्यिका \[\mathbf{AM}\] क्रमश: एक दूसरे त्रिभुज की भुजाओं \[\mathbf{PQ}\] और \[\mathbf{QR}\] तथा माध्यिका \[\mathbf{PN}\] के बराबर हैं। दर्शाइए कि

(image will be uploaded soon)

1. \[\mathbf{\Delta ABM}\cong \mathbf{\Delta PQN}\]

2. \[\mathbf{\Delta ABC}\cong \mathbf{\Delta PQR}\]

उत्तर: \[\Delta ABM\] और \[\Delta PQN\] में

   $AB\text{ }=\text{ }PQ $

   $AM\text{ }=\text{ }PN  $

\[BM\text{ }=\text{ }QN\] (माध्यिका आधार को समद्विभाजित करती है।)

इसलिए, \[\Delta ABM\cong \Delta PQN\]

\[\Delta ABC\] और \[\Delta PQR\] में

 $ AB\text{ }=\text{ }PQ  $

$ BC\text{ }=\text{ }QR  $

\[AC\text{ }=\text{ }PR\] (समान माध्यिका का मतलब है कि तीसरी भुजा बराबर होगी)

इसलिए, \[\Delta ABC\cong \Delta PQR\]

4. \[\mathbf{BE}\] और \[\mathbf{CF}\] एक त्रिभुज \[\mathbf{ABC}\] के दो बराबर शीर्षलम्ब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि \[\mathbf{\Delta ABC}\] एक समद्विबाहु त्रिभुज है।

उत्तर: \[\Delta AEB\] और \[\Delta AFC\] में

\[BE\text{ }=\text{ }CE\] (लम्ब)

\[AB\text{ }=\text{ }BC\] (कर्ण)

इसलिए, \[\Delta AEB\cong \Delta AFC\]

5. \[\mathbf{ABC}\] एक समद्विबाहु त्रिभुज है जिसमें \[\mathbf{AB}\text{ }=\text{ }\mathbf{AC}\] है। \[\mathbf{AP}\bot \mathbf{BC}\] खींच कर दर्शाइए कि \[\angle \mathbf{B}\text{ }=\angle \mathbf{C}\] है।

उत्तर:

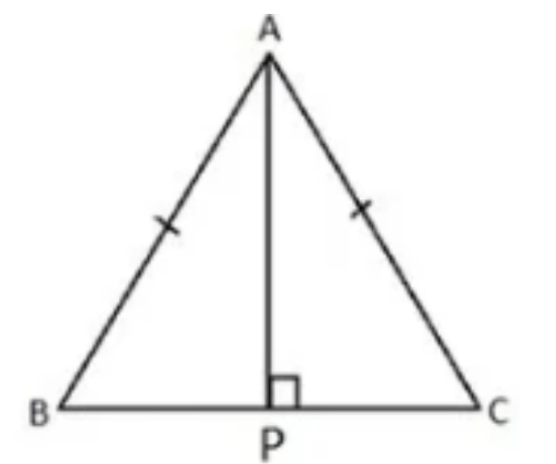
 \[AD\bot BC\] खींचने पर,

\[\Delta APC\] और \[\Delta APB\] मे,

   $ AC\text{ }=\text{ }AB  $

  $ AP\text{ }=\text{ }AP  $

  $ \angle APC\text{ }=\angle APB  $

इसलिए\[,\text{ }\Delta APC\cong \Delta APB\]

इसलिए, \[\angle ACP\text{ }=\angle ABC\]

प्रश्नवाली 7.4

1. दर्शाइए कि एक समकोण त्रिभुज में कर्ण सबसे लम्बी भुजा होती है।

उत्तर: किसी भी समकोण में कर्ण के सामने वाला कोण \[90{}^\circ \] होता है, जबकि अन्य कोण हमेशा \[90{}^\circ \] से कम होते हैं क्योंकि उनका योग \[90{}^\circ \] होता है। हम जानते हैं कि किसी भी त्रिभुज में सबसे बड़े कोण के सामने वाली भुजा सबसे लम्बी होती है। इसलिए समकोण त्रिभुज में कर्ण ही सबसे लम्बी भुजा होती है।

2. दी गई आकृति में, \[\mathbf{\Delta ABC}\] की भुजाओं \[\mathbf{AB}\] और \[\mathbf{AC}\] को क्रमश: बिंदुओं \[\mathbf{P}\] और \[\mathbf{Q}\] तक बढ़ाया गया है। साथ ही, \[\angle \mathbf{PBC}\text{ }<\angle \mathbf{QCB}\] है। दर्शाइए कि \[\mathbf{AC}\text{ }>\text{ }\mathbf{AB}\] है।

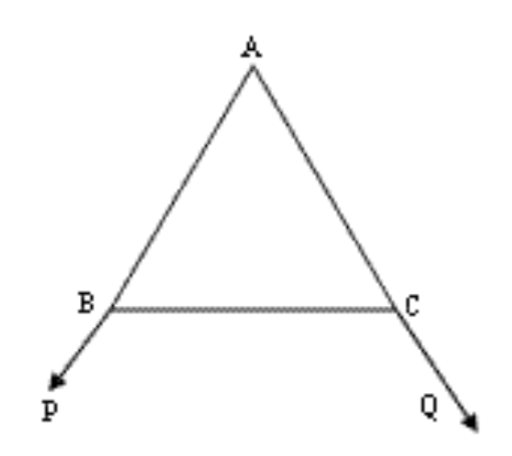
उत्तर: \[\angle ABC\text{ }=\text{ }180{}^\circ \text{ }-\angle PBC\]

\[\angle ACB\text{ }=\text{ }180{}^\circ \text{ }-\angle QCB\]

चूँकि \[\angle PBC\text{ }<\angle OCB\]

इसलिए, \[\angle ABC\text{ }>\angle ACB\]

हम जानते हैं छोटे कोण के सामने वाली भुजा की तुलना में बड़े कोण के सामने वाली भुजा लम्बी होती है। इसलिए, \[AC\text{ }>\text{ }AB\]

3. दी गई आकृति में \[\angle \mathbf{B}\text{ }<\angle \mathbf{A}\] और \[\angle \mathbf{C}\text{ }<\angle \mathbf{D}\] है। दर्शाइए कि \[\mathbf{AD}\text{ }<\text{ }\mathbf{BC}\] है।

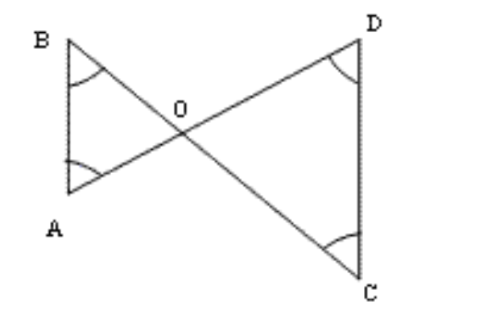
उत्तर: \[AO\text{ }<\text{ }BO\] (छोटे कोण के सामने वाली भुजा)

\[DO\text{ }<\text{ }CO\] (छोटे कोण के सामने वाली भुजा छोटी होती है।)

इसलिए, \[AO\text{ }+\text{ }DO\text{ }<\text{ }BO\text{ }+\text{ }CO\]

या, \[AD\text{ }<\text{ }BC\]

4. \[\text{ }\mathbf{AB}\] और \[\mathbf{CD}\] क्रमश: एक चतुर्भुज \[\mathbf{ABCD}\] की सबसे छोटी और सबसे बड़ी भुजाएँ है। दर्शाइए कि \[\angle \mathbf{A}\text{ }>\angle \mathbf{C}\] और \[\angle \mathbf{B}\text{ }>\angle \mathbf{D}\] है।

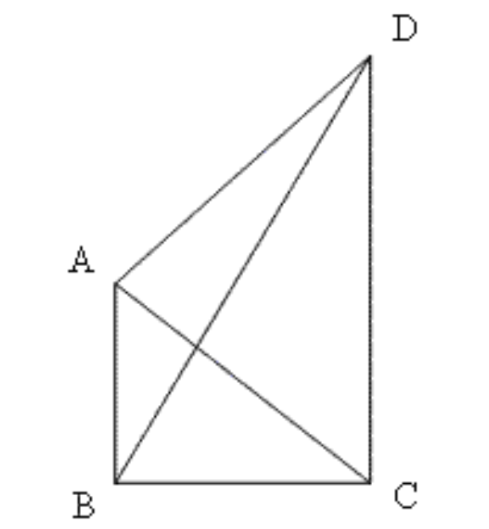
उत्तर: \[BD\] और \[AC\] दो कर्ण खींचिए।

\[\Delta ABD\] में, \[AB\text{ }<\text{ }AD\text{ }<\text{ }BD\]

इसलिए\[,\angle ADB\text{ }<\angle ABD\text{ }............\left( 1 \right)\]

(छोटी भुजा के सामने का कोण छोटा होता है)

\[\Delta BCD\] में, \[BC\text{ }<\text{ }DC\text{ }<\text{ }BD\]

इसलिए, \[\angle BDC<\angle CBD\text{ }...............\left( 2 \right)\]

समीकरण \[(1)\]और \[(2)\]को जोड़ने पर,

\[\angle ADB\text{ }+\angle BDC\text{ }<\angle ABD\text{ }+\angle CBD\]

या, \[\angle ADC\text{ }<\angle ABC\]

इसी तरह\[,\text{ }\Delta ABC\] में

\[\angle BAC\text{ }>\angle ACD\text{ }...............\left( 3 \right)\]

\[\Delta ADC\] में

\[\angle DAC\text{ }>\angle DCA\text{ }............\left( 4 \right)\]

समीकरण \[(3)\]और \[(4)\]को जोड़ने पर,

\[\angle BAC\text{ }+\angle DAC\text{ }>\angle ACB\text{ }+\angle DCA\]

या, \[\angle BAD\text{ }>\angle BCD\]

5. दी गई आकृति में\[,\text{ }\mathbf{PR}\text{ }>\text{ }\mathbf{PQ}\] है और \[\mathbf{PS}\] कोण \[\mathbf{QPR}\] को समद्विभाजित करता है। सिद्ध कीजिए कि \[\angle \mathbf{PSR}\text{ }>\angle \mathbf{PSQ}\] है।

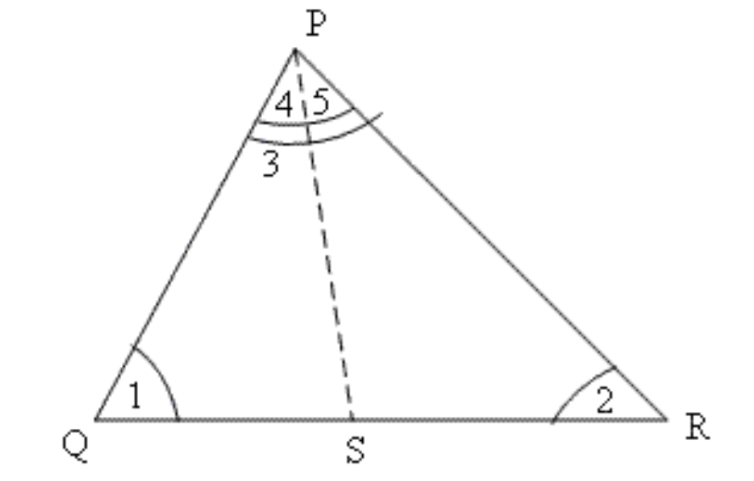
उत्तर:

 सबसे पहले इन कोणों के निम्नलिखित नाम रख लेते हैं:

  $ \angle PQR\text{ }=\text{ }1  $

  $ \angle PRQ\text{ }=\text{ }2  $

   $\angle QPR\text{ }=\text{ }3  $

   $\angle QPS\text{ }=\text{ }4  $

   $\angle RPS\text{ }=\text{ }5  $

   $\angle PSQ\text{ }=\text{ }6  $

   $\angle PSR\text{ }=\text{ }7  $

चूँकि \[PR\text{ }>\text{ }PQ\]

इसलिए, \[\angle 1\text{ }>\angle 2\]

\[\Delta PQS\] में

\[\angle 1\text{ }+\angle 4\text{ }+\angle 6\text{ }=\text{ }180{}^\circ \]

\[\Delta PRS\] में

\[\angle 2\text{ }+\angle 5\text{ }+\angle 7\text{ }=\text{ }180{}^\circ \]

दोनों त्रिभुज में

$   \angle 4\text{ }=\angle 5  $

  $ \angle 1\text{ }>\angle 2  $

इसलिए कोणों का योग \[180{}^\circ \]करने के लिए निम्नलिखित हमेशा सत्य होगा:

\[\angle 6\text{ }<\angle 7\]

6. दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं उनमें लम्ब रेखाखंड सबसे छोटा होता है।

उत्तर:

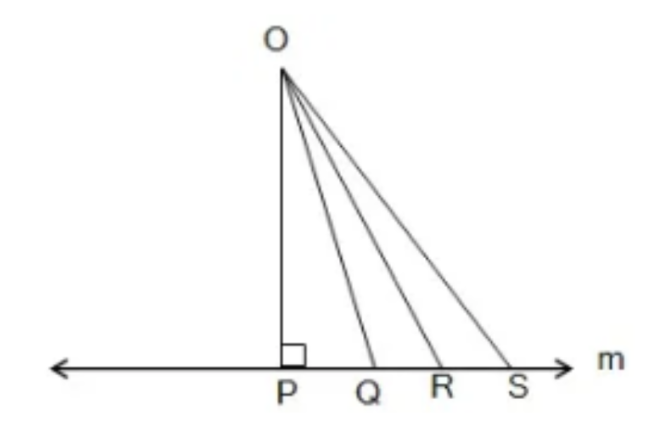
एक रेखा खींचिए। उस पर किसी बिंदु से एक लम्ब डालिए। उसके बाद उसी बिंदु से रेखा के किसी भी अन्य बिंदु पर यदि रेखा खींची जाए तो एक समकोण त्रिभुज बनता है। ऐसे में बाहरी बिंदु से खींची गई दूसरी रेखा उस त्रिभुज का कर्ण होगी। कर्ण हमेशा लम्ब से लम्बी होती है।

NCERT Solutions for Class 9 Maths Chapter 7 Triangles In Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 9 Maths Chapter 7 solution Hindi medium is created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 9 Maths Chapter 7 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 9 Maths Chapter 7 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 9 Maths Triangles solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that. 

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 9 Maths Triangles in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 9 can download these solutions at any time as per their convenience for self-study purpose. 

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 9 Maths in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.