Question

A cricket stump is in the shape of a cylinder surmounted by a cone. The diameter of the cylinder and the total height of the stump are 10 cm and 80 cm respectively. If the height of the conical part is 12 cm, then find its total surface area.

Answer 1

Hint: We will first find the total surface area of the cylinder using the formula, $2\pi r\left( {r + h} \right)$, where $r$is the radius of the cylinder and $h$ is the height of the cylinder.
and then find the total surface of the cone using the formula, \[\pi r\left( {l + r} \right)\]. Add the two areas to write the total surface area of the stump. But, the area of the circle where cylinder and cone are joined is counted twice. So we will subtract the circle from the calculated area to get the required answer.

Complete step-by-step answer:
We are given that the cricket stump is in the shape of a cylinder surmounted by a cone.
The diameter of the cylinder and the total height of the stump are 10 cm and 80 cm respectively.

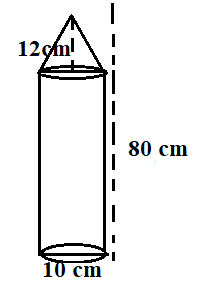
We know that the radius is half the diameter.
Therefore, the radius of the cylinder is $\dfrac{{10}}{2} = 5cm$
The height of the stump is 80 cm, out of which the height of the cone is 12 cm.
Then, the height of the cylinder is $80 - 12 = 68cm$
We will first find the total surface of the cylinder whose radius is 5cm and height is 68 cm.
We know the total surface area of the cylinder is given by $2\pi r\left( {r + h} \right)$, where $r$is the radius of the cylinder and $h$ is the height of the cylinder.
Then, the surface area of the cylinder is
 $
  2\left( {\dfrac{{22}}{7}} \right)\left( 5 \right)\left( {5 + 68} \right) \\
   \Rightarrow \dfrac{{220}}{7}\left( {73} \right) \approx 2,294c{m^2} \\
$
Now, we will find the surface area of the cone, whose radius is 5 cm and height is 12 cm.
The slant of the cone is given by $l = \sqrt {{h^2} + {r^2}} $
Then, slant height of the cone will be $l = \sqrt {{{\left( 5 \right)}^2} + {{\left( {12} \right)}^2}} = 13$
And the total surface area of a cone is given by \[\pi r\left( {l + r} \right)\]
$\Rightarrow$ \[\left( {\dfrac{{22}}{7}} \right)\left( 5 \right)\left( {13 + 5} \right) = 282.85c{m^2}\]
Here, the common surface for cylinder and cone is not the outer surface of the stump. So we will not consider it in the calculation of TSA of stump.
But, the area of the circle where cylinder and cone are joined is counted twice.
Therefore, we will subtract the 2 times area of the circle of the base, that is $2\times\pi {r^2}$, where $r$ is the radius of the circle,
$\Rightarrow$ $2\times\left( {\dfrac{{22}}{7}} \right)\left( 5 \right)\left( 5 \right) = 157.14c{m^2}$
The total surface area of the cricket stump is the sum of the total surface area of the cylinder and cone and then subtract the area of the circle.
$\Rightarrow$ $2,294 + 282.85 - 157.14 \approx 2420c{m^2}$

Hence, the area of the cricket stump is 2420 $c{m^2}$.

Note: We can also do this question by finding the total surface area of the cylinder and then adding it to the curved surface area of the cone. The curved surface of the cone will not include the area of the base of the cone.