Question

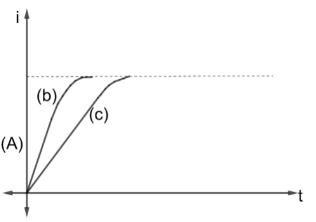
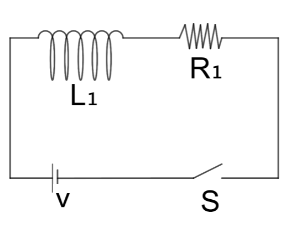
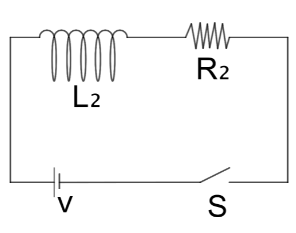
Current growth in two L – R Circuits $(B)$ and $(C)$ is shown in figure $(A)$. Let ${L_1}$, ${L_2}$, ${R_1}$ and ${R_2}$ be the corresponding values in two circuits. Then
(A)

(B)

(C)

A. ${R_1} > {R_2}\:$
B. ${R_1} = {R_2}\:$
C. ${L_1} > {L_2}\:$
D. ${L_1} < {L_2}\:$

Answer 1

Hint:We will firstly observe the graph and then use our concept of steady state current. Then, we will use the concept of current growth in the given circuits. Finally we will arrive at the possible conditions for the given situation.

Formulae Used:
$\tau {\text{ }} = {\text{ }}\dfrac{L}{R}$
\[\Rightarrow I{\text{ }} = {\text{ }}{I_o}{\text{ }}(1{\text{ }} - {\text{ }}{e^{\dfrac{t}{\tau }}})\]

Complete step by step answer:
Firstly, we can observe from the graph that the currents in $(B)$ and $(C)$ reaches the saturation point.
Thus, it follows the condition of saturation current.
${I_o}{\text{ }} = {\text{ }}\dfrac{V}{{{R_1}}}{\text{ }} = {\text{ }}\dfrac{V}{{{R_2}}}$
After further evaluation, we get
${R_1}{\text{ }} = {\text{ }}{R_2}$
Now,
Clearly from the graph, the time when the circuits reach saturation ($\tau $) such that
${\tau _C}{\text{ }} > {\text{ }}{\tau _B}$
Thus, we can say
$\dfrac{{{L_2}}}{{{R_2}}}{\text{ }} > {\text{ }}\dfrac{{{L_1}}}{{{R_1}}}$
But we just found that ${R_1}{\text{ }} = {\text{ }}{R_2}$
Thus, we can say
${L_2}{\text{ }} > {\text{ }}{L_1}$
In other words, we can say
${L_1}{\text{ }} < {\text{ }}{L_2}$

Hence, the correct options are B and D.

Additional Information:
When current passes through an inductor, then the inductor produces an electromotive force called back emf. Its formula is defined as
$\varepsilon {\text{ }} = {\text{ }} - {\text{ }}L\dfrac{{dI}}{{dt}}$
Here, $L$ is the inductance of the inductor, $I$ is the current flowing through the inductor, $\varepsilon $ is the back emf and the negative sign signifies that the produced emf and in turn the induced current opposes the actual current flowing in.

Now, there is another concept called the LR oscillation. Let us understand this.Let us consider a circuit where only there is a resistor, inductor and a switch.Let us consider that initially the resistor is at its peak energy content.Now, when the switch is closed, then due to the back emf of the inductor, it gradually gains all the energy from the resistor and now the resistor is null in energy content whereas the inductor is at its peak.

Again, after a while, the inductor sinks out all its energy and the resistor gradually attains it back. This process continues till the switch is closed. Thus, the energy content oscillates between the inductor and the resistor and thus is called LR oscillation. This is an ideal case which is practically not feasible.

Note:Students should be very careful while concluding something from the graph as it is observed that though the students observe the graph correctly but commits error while concluding a point. Students should also remember that here, the saturation point current for both the currents were the same and thus, we equated the saturation current for both the circuits. This may not be true for all possible circuits. Thus, the students should just take the concept rather than memorizing the whole process. Students should always try to evaluate the answer in a form where each and every step is simplified. This saves their time and effort and also bears a very low chance of any form of errors.