Question

If base of parallelogram is twice it’s height. If the area of parallelogram is \[{\text{72sq}}{\text{.cm}}\].Find its height ?

Answer 1

Hint: We use the given relation of base and height of parallelogram and use the formula to calculate the area of parallelogram as \[{\text{A = b}}{\text{.h}}\]. So , our required solution will be obtained.

Complete step by step answer:

As per given base of a parallelogram is twice its height,
Diagram
  

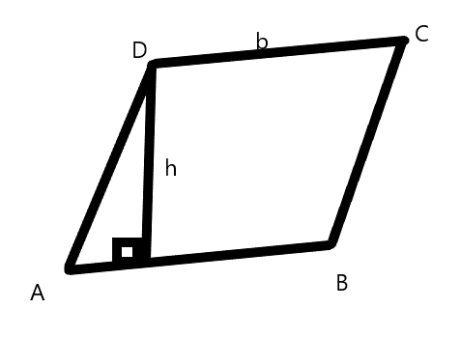
So let the height of the parallelogram be x.
And so the base will be 2x.
Now put the above values in formula of area ,
As \[{\text{A = b}}{\text{.h}}\]
\[
  {\text{A = 2x}}{\text{.x}} \\
   \Rightarrow {\text{72 = 2}}{{\text{x}}^{\text{2}}} \\
   \Rightarrow {{\text{x}}^{\text{2}}}{\text{ = 36}} \\
  {\text{On taking square root, we get,}} \\
  {\text{x = 6cm}} \\
 \]
On substituting the value of x, we get base as \[{\text{2 $\times$ 6 = 12cm}}\] and height as \[{\text{6cm}}\]
Hence , the length of base and height are \[{\text{12cm,6cm}}\].

Note: A parallelogram is a quadrilateral with opposite sides parallel (and therefore opposite angles equal). A quadrilateral with equal sides is called a rhombus, and a parallelogram whose angles are all right angles is called a rectangle.
There are six important properties of parallelograms to know:
1) Opposite sides are congruent (AB = DC).
2) Opposite angles are congruent (D = B).
3) Consecutive angles are supplementary (A + D = 180°).
4) If one angle is right, then all angles are right.
5) The diagonals of a parallelogram bisect each other.
6) Each diagonal of a parallelogram separates it into two congruent triangles.