Question

If the side of a square is tripled, how many times the perimeter of the first square will that of the new square be?

Answer 1

Hint: We start by considering that the side has length x meters for the first square and then if the sides get tripled, then the new square will have 3x meters side. Then as the perimeter is the sum of the sides, we will find the perimeter of the new and the first square. Then to find how many times, the perimeter of the new square is greater than the first square, we will find the ratio of both the perimeters.

Complete step-by-step answer:
We are given that if the side of the square is tripled, then how the perimeter change of the new square is. Let the side of the first square be x meters. Now, if the sides have been tripled, so the new side will be 3 times the first one. So,
New Side of the square = 3x
The perimeter is defined as the total length of the outline of the shape. So in the case of the square perimeter of the square with side x m will be defined as the sum of all the sides.

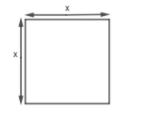
\[\text{Perimeter of first square}=x+x+x+x=4x........\left( i \right)\]
Now, the square has side 3x meters. So, the perimeter of the new square is the sum of its sides.

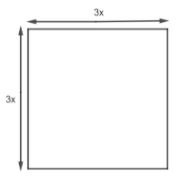
\[\text{Perimeter of new square}=3x+3x+3x+3x=12x........\left( ii \right)\]
Now to find how many times is the new square perimeter to the first square. We will find the ratio of the new square perimeter to the first square perimeter.
Using (i) and (ii), we get,
\[\dfrac{\text{Perimeter of new square}}{\text{Perimeter of first square}}=\dfrac{12x}{4x}\]
Simplifying, we get,
\[\Rightarrow \dfrac{\text{Perimeter of new square}}{\text{Perimeter of first square}}=3\]
So, we get,
\[\Rightarrow \text{Perimeter of new square}=3\times \text{Perimeter of first square}\]
Hence, we get the perimeter of the new square is equal to three times the perimeter of the first square.

Note: We can also find the answer in an alternate method. Let the first square have sides of length x meter. If sides get tripled, then the side of the new square will be 3 times the earlier side.
\[\Rightarrow \text{Side of new square}=3x\]
We know that the formula of the perimeter of the square is \[4\times \text{side}.\]
So, for the new square,
\[\text{Perimeter of square}=4\times \text{side}\]
\[\Rightarrow \text{Perimeter of square}=4\times 3x\]
\[\Rightarrow \text{Perimeter of square}=12x\]
And for the first square,
\[\text{Perimeter of square}=4\times \text{side}\]
\[\Rightarrow \text{Perimeter of square}=4x\]
Now finding the ratio of both the perimeters, we get,
\[\dfrac{\text{Perimeter of new square}}{\text{Perimeter of first square}}=\dfrac{12x}{4x}\]
\[\Rightarrow \dfrac{\text{Perimeter of new square}}{\text{Perimeter of first square}}=3\]
Therefore, the perimeter of the new square is 3 times the perimeter of the first square.