Question

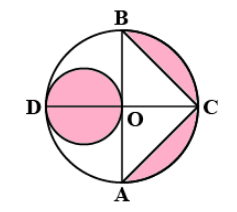
In the figure given below, AB and CD are the two diameters of the circle with center O, which are perpendicular to each other. OB is the diameter of the smaller circle. If OA = 7 cm, then find the area of the shaded region. (Use\[\pi = \dfrac{{22}}{7}\])

Answer 1

Hint: We clearly see that the shades regions are basically two parts, one a circle, whose area we can find directly using the formula for area of circle and the other one is area of triangle ABC is subtracted from the area of semi-circle. Add both the areas and thus, you have your answer.

Complete step-by-step answer:
We are already given that OA = 7 cm.
We can clearly see that OA is the radius of the circle.
Hence, the radius of the circle is 7 cm.
We can also clearly see that OD is also the radius of the circle and it can be seen by the fact that CD is the diameter.
Hence, OD = 7 cm as well.
We see that the smaller circle which is included in the shaded portion has OD as its diameter.
Hence, radius of smaller circle will be determined by the formula:-
\[Radius = \dfrac{{Diameter}}{2}\].
Hence, radius of this smaller circle is \[\dfrac{{Diameter}}{2} = \dfrac{{OD}}{2} = \dfrac{7}{2}cm\].
We know that Area of a circle is given by:-
\[Area = \pi {r^2}\].
Putting the value of $r = \dfrac{7}{2}cm$ in this formula, we have:-
\[Area = \pi {\left( {\dfrac{7}{2}} \right)^2}\]
Since, we are told to use \[\pi = \dfrac{{22}}{7}\]. Let us put this in the formula:-
We will get:- \[Area = \left( {\dfrac{{22}}{7}} \right)\left( {\dfrac{7}{2}} \right)\left( {\dfrac{7}{2}} \right)\]
Now, simplifying it further, we will have:-
\[Area = \left( {\dfrac{{22}}{7}} \right)\left( {\dfrac{7}{2}} \right)\left( {\dfrac{7}{2}} \right)c{m^2} = \dfrac{{22 \times 7}}{{2 \times 2}}c{m^2} = \dfrac{{11 \times 7}}{2}c{m^2} = \dfrac{{77}}{2}c{m^2} = 38.5c{m^2}\].
Hence, the area of the circle which is shaded is 38.5 square cm. ………(1)
Now, we need to find the other region’s area. We can clearly see that if we find the area of a bigger semi-circle and subtract the area of triangle ABC, we will have the required area.
Since, \[Area = \pi {r^2}\].
So, the area of the semi-circle will be given by \[\dfrac{{\pi {r^2}}}{2}\].
Since the radius of the larger circle is 7 cm.
Hence, area of the semicircle is given by \[\dfrac{1}{2} \times \pi \times {(7)^2}c{m^2}\].
$ \Rightarrow \left( {\dfrac{1}{2} \times \dfrac{{22}}{7} \times 7 \times 7} \right)c{m^2}$
$ \Rightarrow \left( {11 \times 7} \right)c{m^2}$
$ \Rightarrow 77c{m^2}$
Hence, the area of the semicircle is 77 square cm. ………(2)
Now, let us find the area of the triangle.
We can see that the triangle has the base AB and the altitude that is height is OC.
AB is the diameter.
So, $AB = 2 \times radius = 2 \times 7 = 14cm$.
And OC is the radius of the circle. So, $OC = 7cm$.
We know that area of triangle is given by:-
$Area = \dfrac{1}{2} \times base \times height$
$ \Rightarrow Area = \left( {\dfrac{1}{2} \times 14 \times 7} \right)c{m^2} = \left( {7 \times 7} \right)c{m^2} = 49c{m^2}$ ………(3)
Hence, the area of the triangle inside the semicircle is given by 49 square cm.
Hence, the area of the shaded region except the circle is the difference of area of semicircle and area of triangle inside the semi-circle.
Now, by using (2) and (3), we have:-
So, Area of semicircles is (77 – 49) square cm. That is 28 square cm. ……..(4)
Now, adding (1) and (4), we have:-
Area of shaded region = (38.5 + 28) square cm that is 46.5 square cm.

Area of shaded region is 46.5m.

Note: The students must keep in mind that they cannot approach this problem directly because the shapes in the shaded region other than the circle is not any fixed shape whose formula we know.
The students must not forget to mention the units while mentioning areas because writing just a number does not mean anything. For example: if we write 5, it does not represent area but only a number.